发展史

卷积神经网络 (Convolutional Neural Network, CNN) 是一种目前广泛用于图像，自然语言处理等领域的深度神经网络模型。1998 年，Lecun 等人 ¹ 提出了一种基于梯度的反向传播算法用于文档的识别。在这个神经网络中，卷积层 (Convolutional Layer) 扮演着至关重要的角色。

随着运算能力的不断增强，一些大型的 CNN 网络开始在图像领域中展现出巨大的优势，2012 年，Krizhevsky 等人 ² 提出了 AlexNet 网络结构，并在 ImageNet 图像分类竞赛 ³ 中以超过之前 11% 的优势取得了冠军。随后不同的学者提出了一系列的网络结构并不断刷新 ImageNet 的成绩，其中比较经典的网络包括：VGG (Visual Geometry Group) ⁴，GoogLeNet ⁵ 和 ResNet ⁶。

CNN 在图像分类问题上取得了不凡的成绩，同时一些学者也尝试将其应用在图像的其他领域，例如：物体检测 ⁷⁸⁹，语义分割 ¹⁰，图像摘要 ¹¹，行为识别 ¹² 等。除此之外，在非图像领域 CNN 也取得了一定的成绩 ¹³。

模型原理

下图为 Lecun 等人提出的 LeNet-5 的网络架构：

下面我们针对 CNN 网络中的不同类型的网络层逐一进行介绍。

输入层

LeNet-5 解决的手写数字分类问题的输入为一张 32x32 像素的灰度图像 (Gray Scale)。日常生活中计算机常用的图像的表示方式为 RGB，即将一张图片分为红色通道 (Red Channel)，绿色通道 (Green Channel) 和蓝色通道 (Blue Channel)，其中每个通道的每个像素点的数值范围为 $\left[0, 255\right]$。灰度图像表示该图片仅包含一个通道，也就是不具备彩色信息，每个像素点的数值范围同 RGB 图像的取值范围相同。

因此，一张图片在计算机的眼里就是一个如下图所示的数字矩阵 (示例图片来自于 MNIST 数据集 ¹⁴)：

在将图像输入到 CNN 网络之前，通常我们会对其进行预处理，因为每个像素点的最大取值为 $255$，因此将每个像素点的值除以 $255$ 则可以将其归一化到 $\left[0, 1\right]$ 的范围。

卷积层

在了解卷积层之前，让我们先来了解一下什么是卷积？设 $f\left(x\right), g\left(x\right)$ 是 $\mathbb{R}$ 上的两个可积函数，则卷积定义为：

$$ \left(f * g\right) \left(x\right) = \int_{- \infty}^{\infty}{f \left(\tau\right) g \left(x - \tau\right) d \tau} $$

离散形式定义为：

$$ \left(f * g\right) \left(x\right) = \sum_{\tau = - \infty}^{\infty}{f \left(\tau\right) g \left(x - \tau\right)} $$

我们用一个示例来形象的理解一下卷积的含义，以离散的形式为例，假设我们有两个骰子，$f\left(x\right), g\left(x\right)$ 分别表示投两个骰子，$x$ 面朝上的概率。

$$ f \left(x\right) = g \left(x\right) = \begin{cases} 1/6 & x = 1, 2, 3, 4, 5, 6 \\ 0 & \text{otherwise} \end{cases} $$

卷积 $\left(f * g\right) \left(x\right)$ 表示投两个骰子，朝上数字之和为 $x$ 的概率。则和为 $4$ 的概率为：

$$ \begin{equation} \begin{split} \left(f * g\right) \left(4\right) &= \sum_{\tau = 1}^{6}{f \left(\tau\right) g \left(4 - \tau\right)} \\ &= f \left(1\right) g \left(4 - 1\right) + f \left(2\right) g \left(4 - 2\right) + f \left(3\right) g \left(4 - 3\right) \\ &= 1/6 \times 1/6 + 1/6 \times 1/6 + 1/6 \times 1/6 \\ &= 1/12 \end{split} \end{equation} $$

这是一维的情况，我们处理的图像为一个二维的矩阵，因此类似的有：

$$ \left(f * g\right) \left(x, y\right) = \sum_{v = - \infty}^{\infty}{\sum_{h = - \infty}^{\infty}{f \left(h, v\right) g \left(x - h, y - v\right)}} $$

这次我们用一个抽象的例子解释二维情况下卷积的计算，设 $f, g$ 对应的概率矩阵如下：

$$ f = \left[ \begin{array}{ccc} \color{red}{a_{0, 0}} & \color{orange}{a_{0, 1}} & \color{yellow}{a_{0, 2}} \\ \color{green}{a_{1, 0}} & \color{cyan}{a_{1, 1}} & \color{blue}{a_{1, 2}} \\ \color{purple}{a_{2, 0}} & \color{black}{a_{2, 1}} & \color{gray}{a_{2, 2}} \end{array} \right] , g = \left[ \begin{array}{ccc} \color{gray}{b_{-1, -1}} & \color{black}{b_{-1, 0}} & \color{purple}{b_{-1, 1}} \\ \color{blue}{b_{0, -1}} & \color{cyan}{b_{0, 0}} & \color{green}{b_{0, 1}} \\ \color{yellow}{b_{1, -1}} & \color{orange}{b_{1, 0}} & \color{red}{b_{1, 1}} \end{array} \right] $$

则 $\left(f * g\right) \left(1, 1\right)$ 计算方式如下：

$$ \left(f * g\right) \left(1, 1\right) = \sum_{v = 0}^{2}{\sum_{h = 0}^{2}{f \left(h, v\right) g \left(1 - h, 1 - v\right)}} $$

从这个计算公式中我们就不难看出为什么上面的 $f, g$ 两个概率矩阵的角标会写成上述形式，即两个矩阵相同位置的角标之和均为 $1$。$\left(f * g\right) \left(1, 1\right)$ 即为 $f, g$ 两个矩阵中对应颜色的元素乘积之和。

在上例中，$f, g$ 两个概率矩阵的大小相同，而在 CNN 中，$f$ 为输入的图像，$g$ 一般是一个相对较小的矩阵，我们称之为卷积核。这种情况下，卷积的计算方式是类似的，只是会将 $g$ 矩阵旋转 $180^{\circ}$ 使得相乘的元素的位置也相同，同时需要 $g$ 在 $f$ 上进行滑动并计算对应位置的卷积值。下图 ¹⁵ 展示了一步计算的具体过程：

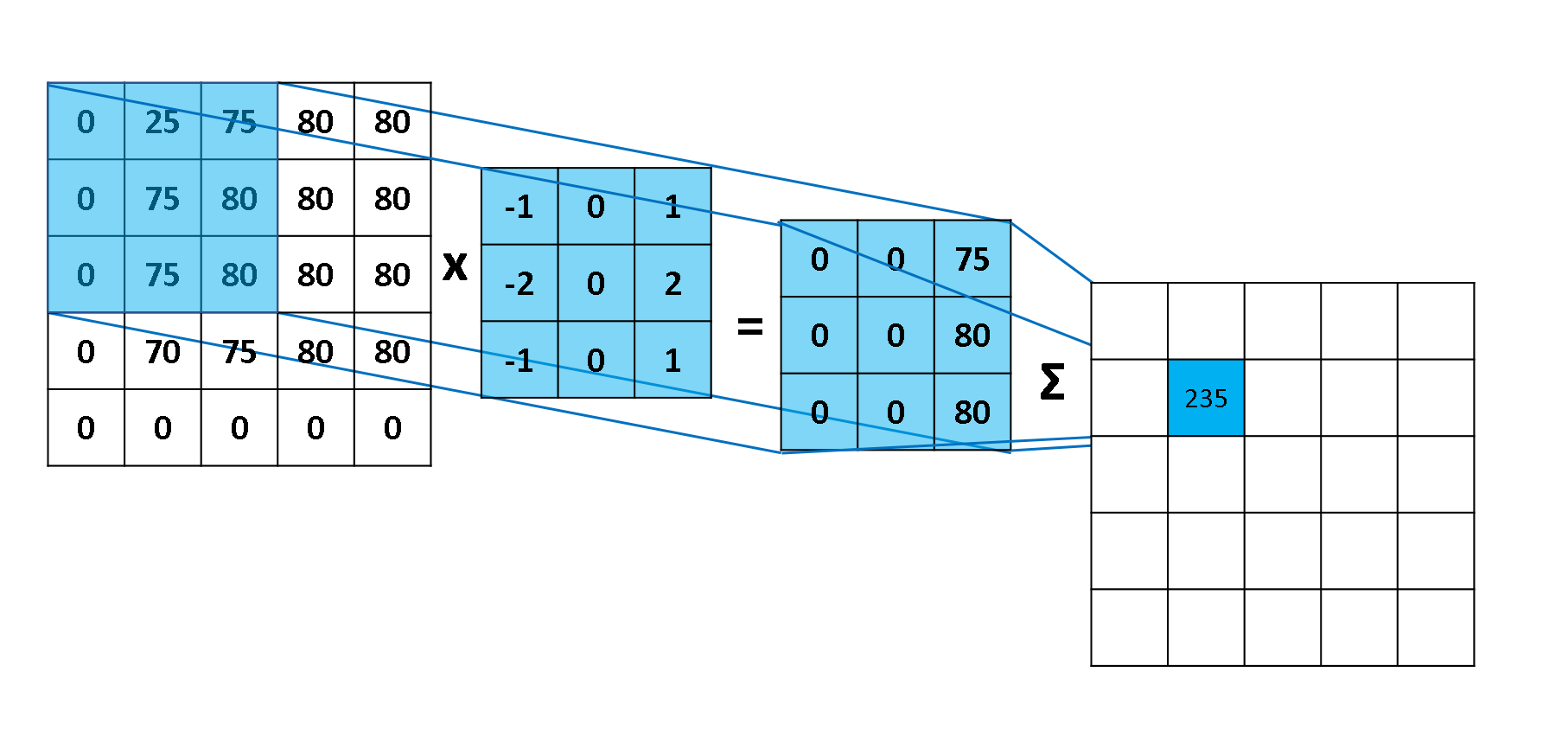
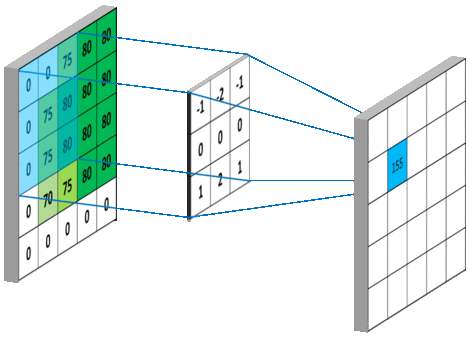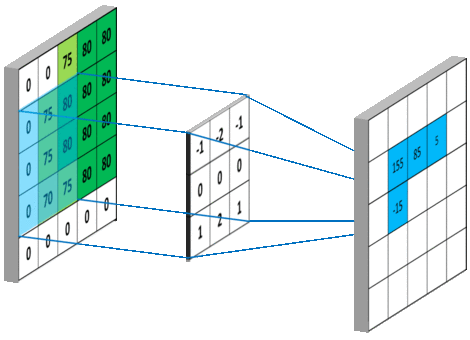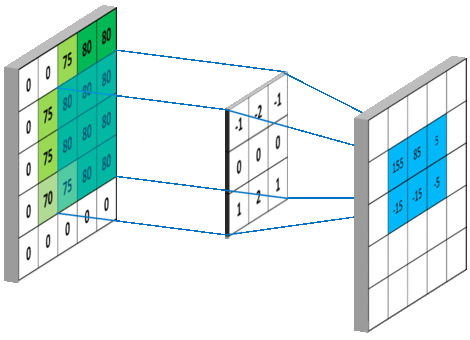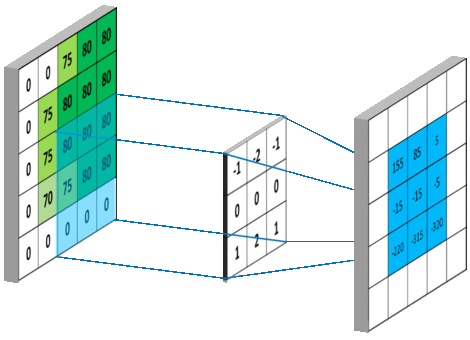
下图 ¹⁵ 形象的刻画了利用一个 3x3 大小的卷积核的整个卷积计算过程：

一些预设的卷积核对于图片可以起到不同的滤波器效果，例如下面 4 个卷积核分别会对图像产生不同的效果：不改变，边缘检测，锐化和高斯模糊。

$$ \left[ \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array} \right] , \left[ \begin{array}{ccc} -1 & -1 & -1 \\ -1 & 8 & -1 \\ -1 & -1 & -1 \end{array} \right] , \left[ \begin{array}{ccc} 0 & -1 & 0 \\ -1 & 5 & -1 \\ 0 & -1 & 0 \end{array} \right] , \dfrac{1}{16} \left[ \begin{array}{ccc} 1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1 \end{array} \right] $$

对 lena 图片应用这 4 个卷积核，变换后的效果如下 (从左到右，从上到下)：

在上面整个计算卷积的动图中，我们不难发现，利用 3x3 大小 (我们一般将这个参数称之为 kernel_size，即卷积核的大小，其可以为一个整数表示长宽大小相同，也可以为两个不同的整数) 的卷积核对 5x5 大小的原始矩阵进行卷积操作后，结果矩阵并没有保持原来的大小，而是变为了 (5-(3-1))x(5-(3-1)) (即 3x3) 大小的矩阵。这就需要引入 CNN 网络中卷积层的两个常用参数 padding 和 strides。

padding 是指是否对图像的外侧进行补零操作，其取值一般为 VALID 和 SAME 两种。VALID 表示不进行补零操作，对于输入形状为 $\left(x, y\right)$ 的矩阵，利用形状为 $\left(m, n\right)$ 的卷积核进行卷积，得到的结果矩阵的形状则为 $\left(x-m+1, y-n+1\right)$。SAME 表示进行补零操作，在进行卷积操作前，会对图像的四个边缘分别向左右补充 $\left(m \mid 2 \right) + 1$ 个零，向上下补充 $\left(n \mid 2 \right) + 1$ 个零 ($\mid$ 表示整除)，从而保证进行卷积操作后，结果的形状与原图像的形状保持相同，如下图 ¹⁵ 所示：

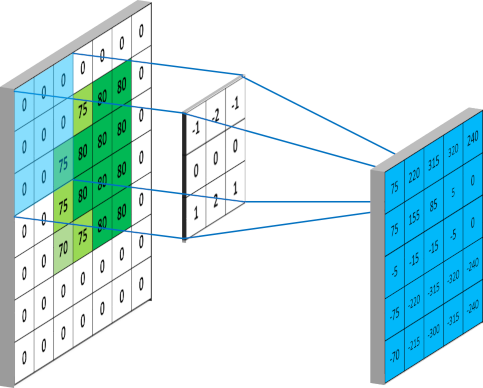
strides 是指进行卷积操作时，每次卷积核移动的步长。示例中，卷积核在横轴和纵轴方向上的移动步长均为 $1$，除此之外用于也可以指定不同的步长。移动的步长同样会对卷积后的结果的形状产生影响。

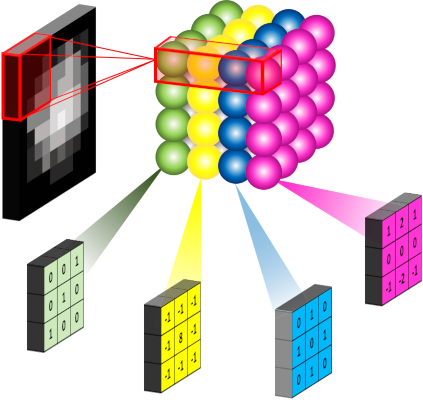
除此之外，还有另一个重要的参数 filters，其表示在一个卷积层中使用的卷积核的个数。在一个卷积层中，一个卷积核可以学习并提取图像的一种特征，但往往图片中包含多种不同的特征信息，因此我们需要多个不同的卷积核提取不同的特征。下图 ¹⁵ 是一个利用 4 个不同的卷积核对一张图像进行卷积操作的示意图：

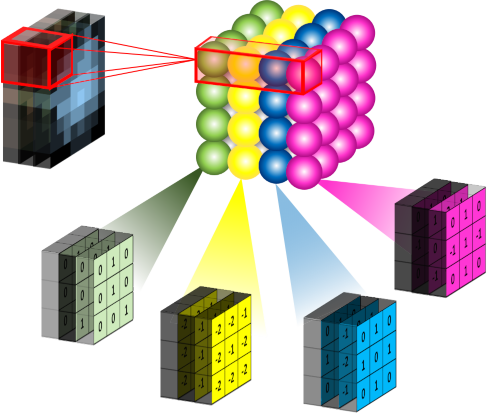
上面我们都是以一个灰度图像 (仅包含 1 个通道) 为示例进行的讨论，那么对于一个 RGB 图像 (包含 3 个通道)，相应的，卷积核也是一个 3 维的形状，如下图 ¹⁵ 所示：

卷积层对于我们的神经网络的模型带来的改进主要包括如下三个方面：稀疏交互 (sparse interactions)，参数共享 (parameter sharing) 和等变表示 (equivariant representations)。

在全连接的神经网络中，隐含层中的每一个节点都和上一层的所有节点相连，同时有被连接到下一层的全部节点。而卷积层不同，节点之间的连接性受到卷积核大小的制约。下图 ¹⁶ 分别以自下而上 (左) 和自上而下 (右) 两个角度对比了卷积层和全连接层节点之间连接性的差异。

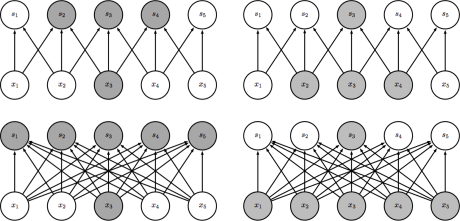
在上图 (右) 中，我们可以看出节点 $s_3$ 受到节点 $x_2$，$x_3$ 和 $x_4$ 的影响，这些节点被称之为 $s_3$ 的接受域 (receptive field)。稀疏交互使得在 $m$ 个输入和 $n$ 个输出的情况下，参数的个数由 $m \times n$ 个减少至 $k \times n$ 个，其中 $k$ 为卷积核的大小。尽管一个节点在一个层级之间仅与其接受域内的节点相关联，但是对于深层中的节点，其与绝大部分输入之间却存在这间接交互，如下图 ¹⁶ 所示：

节点 $g_3$ 尽管直接的连接是稀疏的，但处于更深的层中可以间接的连接到全部或者大部分的输入节点。这就使得网络可以仅通过这种稀疏交互来高效的描述多个输入变量之间的复杂关系。

除了稀疏交互带来的参数个数减少外，参数共享也起到了类似的作用。所谓参数共享就是指在进行不同操作时使用相同的参数，具体而言也就是在我们利用卷积核在图像上滑动计算卷积时，每一步使用的卷积核都是相同的。同全连接网络的情况对比如下图 ¹⁶ 所示：

在全连接网络 (上图 - 下) 中，任意两个节点之间的连接 (权重) 仅用于这两个节点之间，而在卷积层中，如上图所示，其对卷积核中间节点 (黑色箭头) 的使用方式 (权重) 是相同的。参数共享虽然对于计算的时间复杂度没有带来改进，仍然是 $O \left(k \times n\right)$，但其却将参数个数降低至 $k$ 个。

正是由于参数共享机制，使得卷积层具有平移 等变 (equivariance) 的性质。对于函数 $f\left(x\right)$ 和 $g\left(x\right)$，如果满足 $f\left(g\left(x\right)\right) = g\left(f\left(x\right)\right)$，我们就称 $f\left(x\right)$ 对于变换 $g$ 具有等变性。简言之，对于图像如果我们将所有的像素点进行移动，则卷积后的输出表示也会移动同样的量。

非线性层

非线性层并不是 CNN 特有的网络层，在此我们不再详细介绍，一般情况下我们会使用 ReLU 作为我们的激活函数。

池化层

池化层 是一个利用 池化函数 (pooling function) 对网络输出进行进一步调整的网络层。池化函数使用某一位置的相邻输出的总体统计特征来代替网络在该位置的输出。常用的池化函数包括最大池化 (max pooling) 函数 (即给出邻域内的最大值) 和平均池化 (average pooling) 函数 (即给出邻域内的平均值) 等。但无论选择何种池化函数，当对输入做出少量平移时，池化对输入的表示都近似 不变 (invariant)。局部平移不变性 是一个很重要的性质，尤其是当我们关心某个特征是否出现而不关心它出现的位置时。

池化层同卷积层类似，具有三个比较重要的参数：pool_size，strides 和 padding，分别表示池化窗口的大小，步长以及是否对图像的外侧进行补零操作。下图 ¹⁶ 是一个 pool_size=3，strides=3，padding='valid' 的最大池化过程示例：

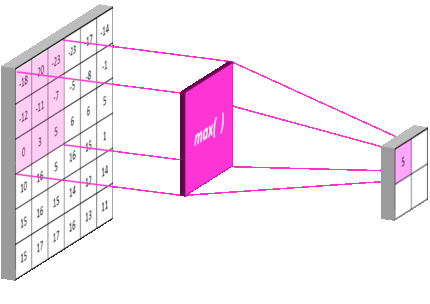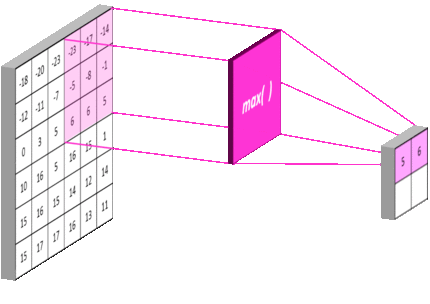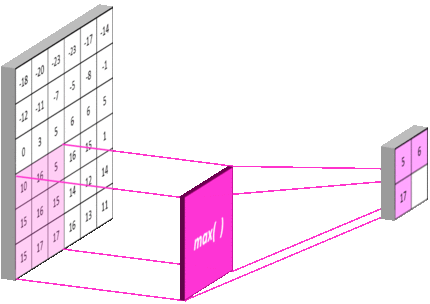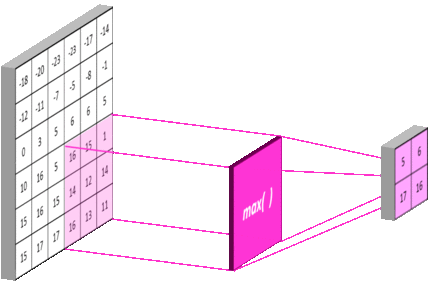
池化层同时也能够提高网络的计算效率，例如上图中在横轴和纵轴的步长均为 $3$，经过池化后，下一层网络节点的个数降低至前一层的 $\frac{1}{3 \times 3} = \frac{1}{9}$。

全连接层

全链接层 (Fully-connected or Dense Layer) 的目的就是将我们最后一个池化层的输出连接到最终的输出节点上。例如，最后一个池化层的输出大小为 $\left[5 \times 5 \times 16\right]$，也就是有 $5 \times 5 \times 16 = 400$ 个节点，对于手写数字识别的问题，我们的输出为 0 至 9 共 10 个数字，采用 one-hot 编码的话，输出层共 10 个节点。例如在 LeNet 中有 2 个全连接层，每层的节点数分别为 120 和 84，在实际应用中，通常全连接层的节点数会逐层递减。需要注意的是，在进行编码的时候，第一个全连接层并不是直接与最后一个池化层相连，而是先对池化层进行 flatten 操作，使其变成一个一维向量后再与全连接层相连。

输出层

输出层根据具体问题的不同会略有不同，例如对于手写数字识别问题，采用 one-hot 编码的话，输出层则包含 10 个节点。对于回归或二分类问题，输出层则仅包含 1 个节点。当然对于二分类问题，我们也可以像多分类问题一样将其利用 one-hot 进行编码，例如 $\left[1, 0\right]$ 表示类型 0，$\left[0, 1\right]$ 表示类型 1。

扩展与应用

本节我们将介绍一些经典的 CNN 网络架构及其相关的改进。

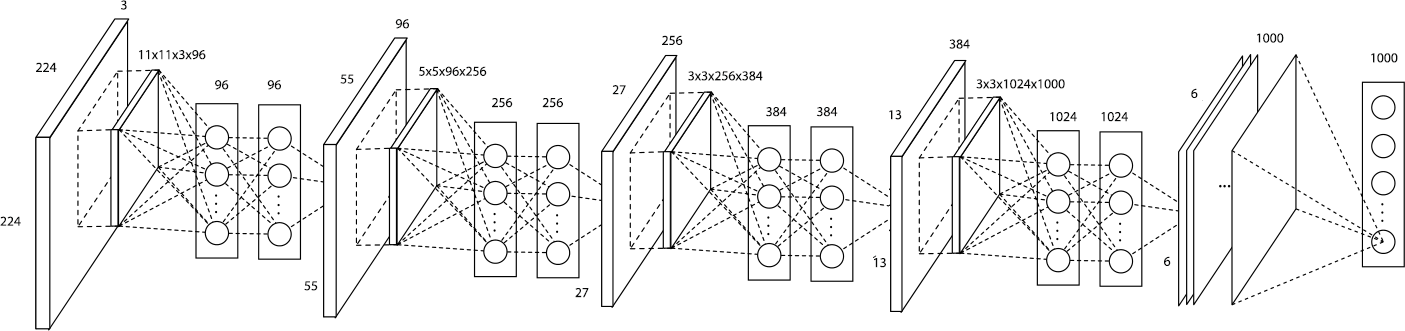
AlexNet ²

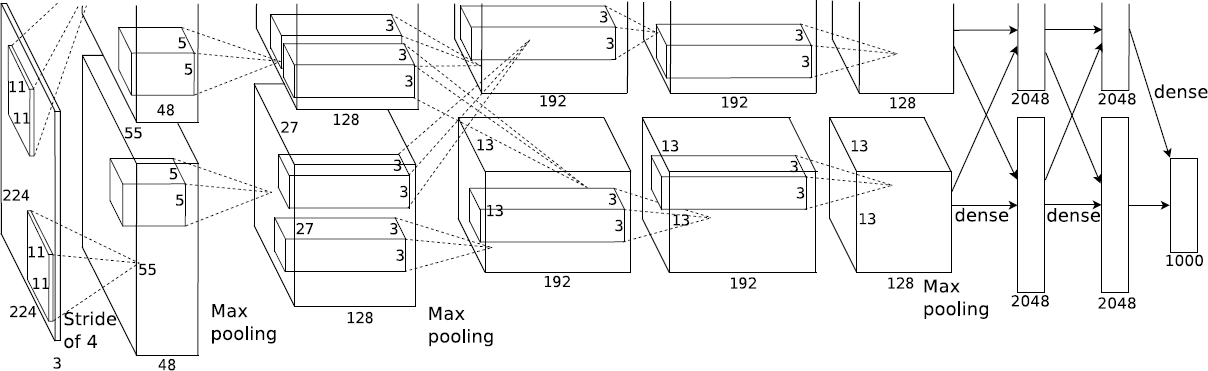
AlexNet 在整体结构上同 LeNet-5 类似，其改进大致如下：

• 网络包含了 5 个卷积层和 3 个全连接层，网络规模变大。
• 使用了 ReLU 非线性激活函数。
• 应用了 Data Augmentation，Dropout，Momentum，Weight Decay 等策略改进训练。
• 在算力有限的情况下，对模型进行划分为两部分并行计算。
• 增加局部响应归一化 (LRN, Local Response Normalization)。

LRN 的思想来自与生物学中侧抑制 (Lateral Inhibition) 的概念，简单来说就是相近的神经元之间会发生抑制作用。在 AlexNet 中，给出的 LRN 计算公式如下：

$$ b_{x,y}^{i} = a_{x,y}^{i} / \left(k + \alpha \sum_{j = \max \left(0, i - n/2\right)}^{\min \left(N - 1, i + n/2\right)}{\left(a_{x,y}^{j}\right)^2}\right)^{\beta} $$

其中，$a_{x,y}^{i}$ 表示第 $i$ 个卷积核在位置 $\left(x,y\right)$ 的输出，$N$ 为卷积核的个数，$k, n, \alpha, \beta$ 均为超参数，在原文中分别初值为：$k=2, n=5, \alpha=10^{-4}, \beta=0.75$。在上式中，分母为所有卷积核 (Feature Maps) 的加和，因此 LRN 可以简单理解为一个跨 Feature Maps 的像素级归一化。

开源实现：

• tensorflow/models, tflearn/examples
• pytorch/torchvision/models
• caffe2/models
• incubator-mxnet/example

VGG Net ⁴

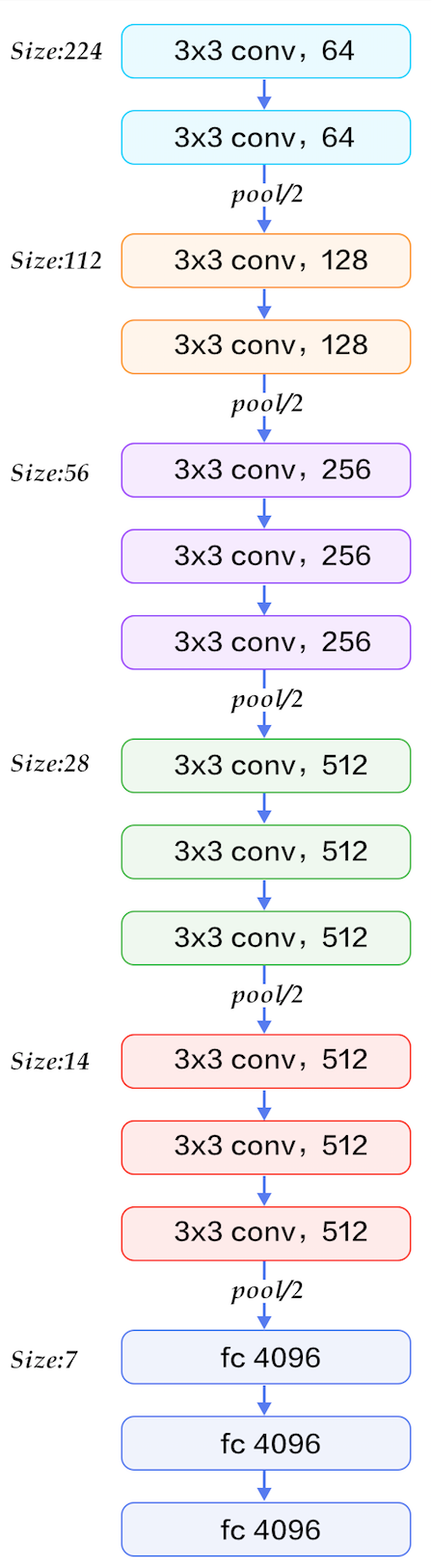
左图是 VGG-16 Net 的网络结构，原文中还有一个 VGG-19 Net，其差别在于后面三组卷积层中均多叠加了一个卷积层，使得网络层数由 16 增加至 19。

VGG Net 的主要改变如下：

• 网络层级更深，从 AlexNet 的 8 层增加至 16 层和 19 层，更深的网络层级意味着更强的学习能力，但也需要更多的算力对模型进行优化。
• 仅使用 3x3 大小的卷积。在 AlexNet 中，浅层部分使用了较大的卷积核，而 VGG 使用了 3x3 的小卷积核进行串联叠加，减少了参数个数。
• 卷积采样的步长为 1x1，Max Pooling 的步长为 2x2。
• 去掉了效果提升不明显的但计算耗时的 LRN。
• 增加了 Feature Maps 的个数。

开源实现：

• tensorflow/models, tflearn/examples, tensorlayer/awesome-tensorlayer
• tf/keras/applications, keras/applications
• pytorch/torchvision/models
• caffe2/models
• incubator-mxnet/example

Network in Network (NIN) ¹⁷

NIN 网络的主要改变如下：

• 利用多层的全连接网络替换线性的卷积，即 mlpconv (Conv + MLP) 层。其中卷积层为线性的操作，而 MLP 为非线性的操作，因此具有更高的抽象能力。
• 去掉了全连接层，使用 Global Average Pooling，也就是将每个 Feature Maps 上所有的值求平均，直接作为输出节点，如下图所示：

• 相比 AlexNet 简化了网络结构，仅包含 4 个 NIN 单元和一个 Global Average Pooling，整个参数空间比 AlexNet 小了一个数量级。

在 NIN 中，在跨通道的情况下，mlpconv 层又等价于传统的 Conv 层后接一个 1x1 大小的卷积层，因此 mlpconv 层有时也称为 cccp (cascaded cross channel parametric pooling) 层。1x1 大小的卷积核可以说实现了不同通道信息的交互和整合，同时对于输入通道为 $m$ 和输出通道为 $n$，1x1 大小的卷积核在不改变分辨率的同时实现了降维 ($m > n$ 情况下) 或升维 ($m < n$ 情况下) 操作。

开源实现：

• tflearn/examples

GoogLeNet (Inception V1) ⁵, Inception V3 ¹⁸, Inception V4 ¹⁹

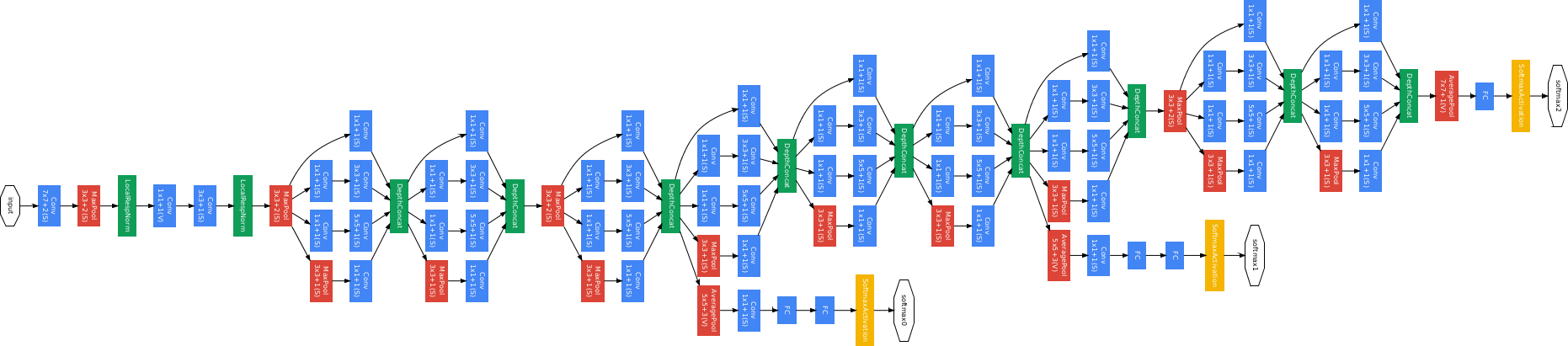
除了 VGG 这种从网络深度方向进行优化的策略以外，Google 还提出了在同一层利用不同大小的卷积核同时提取不同特征的思路，对于这样的结构我们称之为 Inception。

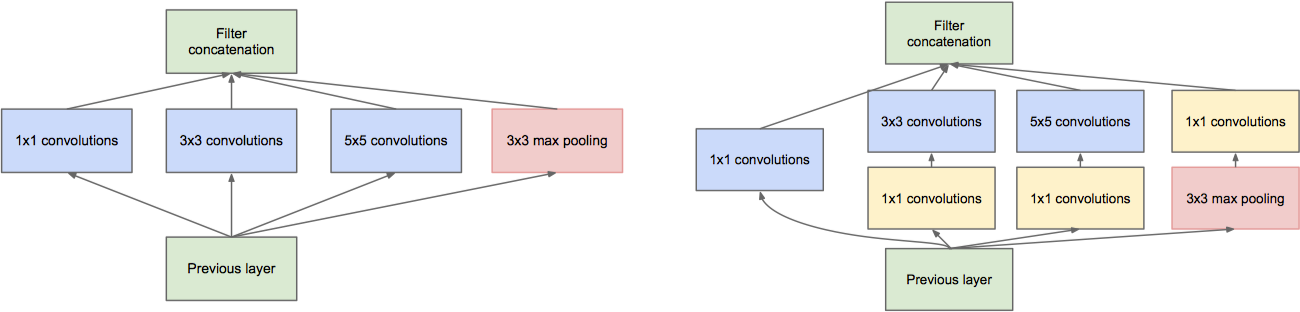
上图 (左) 为原始的 Inception 结构，在这样一层中分别包括了 1x1 卷积，3x3 卷积，5x5 卷积和 3x3 Max Polling，使得网络在每一层都能学到不同尺度的特征。最后通过 Filter Concat 将其拼接为多个 Feature Maps。

这种方式虽然能够带来性能的提升，但同时也增加了计算量，因此为了进一步改善，其选择利用 1x1 大小的卷积进行降维操作，改进后的 Inception 模块如上图 (右) 所示。我们以 GoogLeNet 中的 inception (3a) 模块为例 (输入大小为 28x28x192)，解释 1x1 卷积的降维效果。

对于原始 Inception 模块，1x1 卷积的通道为 64，3x3 卷积的通道为 128，5x5 卷积的通道为 32，卷积层的参数个数为：

$$ \begin{equation} \begin{split} \# w_{\text{3a_conv_without_1x1}} =& 1 \times 1 \times 192 \times 64 \\ & + 3 \times 3 \times 192 \times 128 \\ & + 5 \times 5 \times 192 \times 32 \\ =& 387072 \end{split} \end{equation} $$

对于加上 1x1 卷积后的 Inception 模块 (通道数分别为 96 和 16) 后，卷积层的参数个数为：

$$ \begin{equation} \begin{split} \# w_{\text{3a_conv_with_1x1}} =& 1 \times 1 \times 192 \times 64 \\ & + 1 \times 1 \times 192 \times 96 + 3 \times 3 \times 96 \times 128 \\ & + 1 \times 1 \times 192 \times 16 + 5 \times 5 \times 16 \times 32 \\ =& 157184 \end{split} \end{equation} $$

可以看出，在添加 1x1 大小的卷积后，参数的个数减少了 2 倍多。通过 1x1 卷积对特征进行降维的层称之为 Bottleneck Layer 或 Bottleneck Block。

在 GoogLeNet 中，作者还提出了 Auxiliary Classifiers (AC)，用于辅助训练。AC 通过增加浅层的梯度来减轻深度梯度弥散的问题，从而加速整个网络的收敛。

随后 Google 在此对 Inception 进行了改进，同时提出了卷积神经网络的 4 项设计原则，概括如下：

1. 避免表示瓶颈，尤其是在网络的浅层部分。一般来说，在到达任务的最终表示之前，表示的大小应该从输入到输出缓慢减小。
2. 高维特征在网络的局部更容易处理。在网络中增加更多的非线性有助于获得更多的解耦特征，同时网络训练也会加快。
3. 空间聚合可以在低维嵌入中进行，同时也不会对表征能力带来太多影响。例如，再进行尺寸较大的卷积操作之前可以先对输入进行降维处理。
4. 在网络的宽度和深度之间进行权衡。通过增加网络的深度和宽度均能够带来性能的提升，在同时增加其深度和宽度时，需要综合考虑算力的分配。

Inception V3 的主要改进包括：

• 增加了 Batch Normalized 层。
• 将一个 5x5 的卷积替换为两个串联的 3x3 的卷积 (基于原则 3)，减少了网络参数，如下图所示：

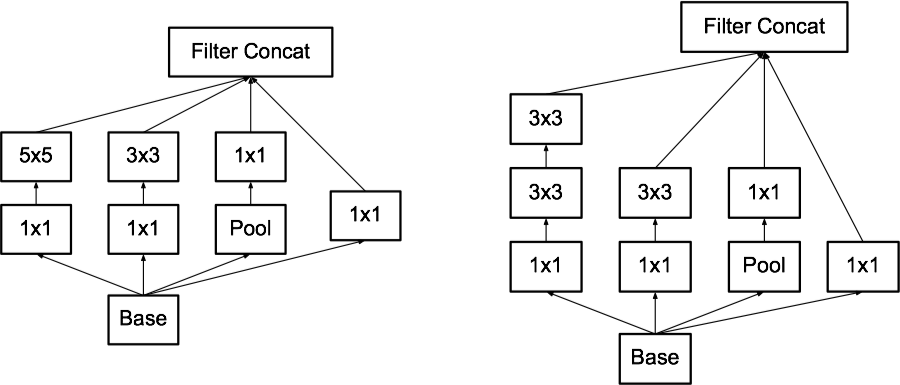
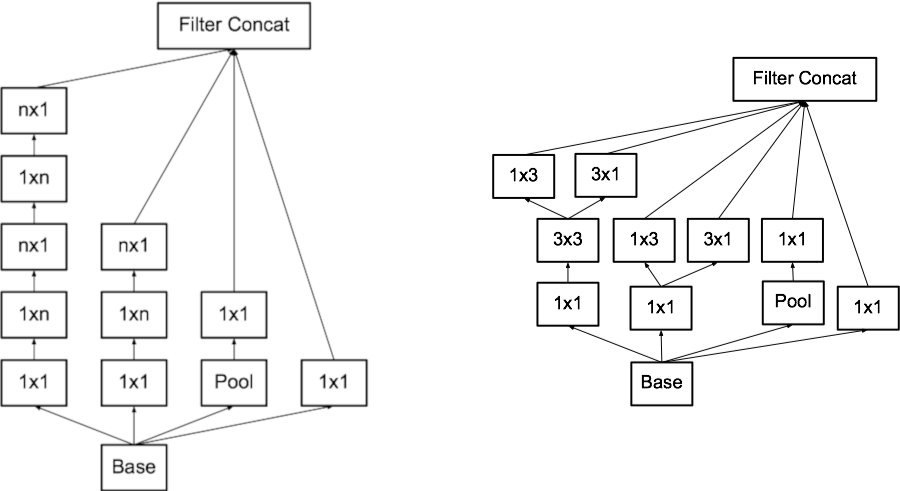
• 利用串联的 1xn 和 nx1 的非对称卷积 (Asymmetric Convolutions) 替代 nxn 的卷积 (基于原则 3)，减少了网络参数，如下图 (左) 所示：
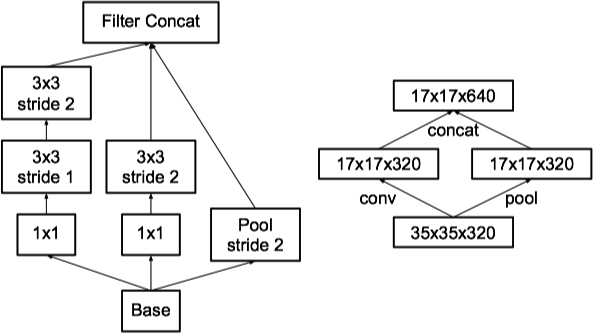
• 增加带有滤波器组 (filter bank) 的 Inception 模块 (基于原则 2)，用于提升高维空间的表示能力，如下图 (右) 所示：

• 重新探讨了 Auxiliary Classifiers 的作用，发现其在训练初期并没有有效的提高收敛速度，尽在训练快结束时会略微提高网络的精度。
• 新的下采样方案。在传统的做法中，如果先进行 Pooling，在利用 Inception 模块进行操作，如下图 (左) 所示，会造成表示瓶颈 (原则 1)；而先利用 Inception 模块进行操作，再进行 Pooling，则会增加参数数量。
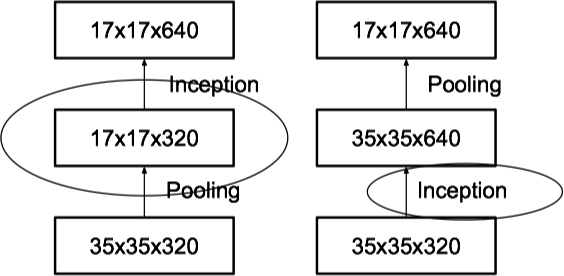
  因此，借助 Inception 结构的思想，作者提出了一种新的下采样方案。下图 (左) 是利用 Inception 的思想进行下采样的内部逻辑，下图 (右) 为同时利用 Inception 思想和 Pooling 进行下采样的整体框架。

• Label Smoothing 机制。假设标签的真实分布为 $q\left(k\right)$，则对于一个真实标签 $y$ 而言，有 $q\left(y\right) = 1$，对于 $k \neq y$，有 $q\left(k\right) = 0$。这种情况会导致两个问题：一个是当模型对于每个训练样本的真实标签赋予全部的概率时，模型将会发生过拟合；另一个是其鼓励拉大最大概率标签同其他标签之间的概率差距，从而降低网络的适应性。也就是说这种情况的发生是由于网络对于其预测结果过于自信。因此，对于一个真实标签 $y$，我们将其标签的分布 $q\left(k | x\right) = \delta_{k, y}$ 替换为： $$ q' \left(k | x\right) = \left(1 - \epsilon\right) \delta_{k, y} + \epsilon u \left(k\right) $$ 其中，$u \left(k\right)$ 是一个固定的分布，文中采用了均匀分布，即 $u \left(k\right) = 1 / K$；$\epsilon$ 为权重项，试验中取为 $0.1$。

Inception V4 对于 Inception 网络做了进一步细致的调整，其主要是将 Inception V3 中的前几层网络替换为了 stem 模块，具体的 stem 模块结构就不在此详细介绍了。

开源实现：

• tensorflow/models, tflearn/examples, tensorlayer/awesome-tensorlayer
• tf/keras/applications, keras/applications
• pytorch/torchvision/models
• caffe2/models
• incubator-mxnet/example

Deep Residual Net ⁶, Identity Mapping Residual Net ²⁰, DenseNet ²¹

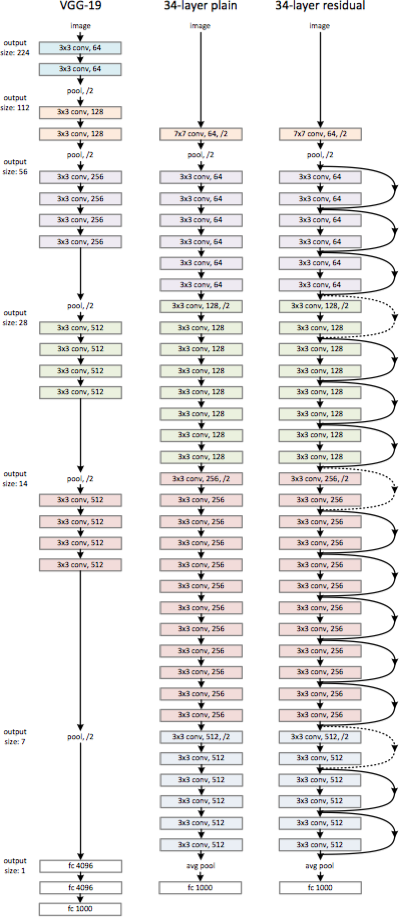
随着网络深度的不断增加啊，其效果并未如想象一般提升，甚至发生了退化，He 等人 ⁶ 发现在 CIFAR-10 数据集上，一个 56 层的神经网络的性能要比一个 20 层的神经网络要差。网络层级的不断增加，不仅导致参数的增加，同时也可能导致梯度弥散问题 (vanishing gradients)。

这对这些问题，He 等人提出了一种 Deep Residual Net，在这个网络结构中，残差 (residual) 的思想可以理解为：假设原始潜在的映射关系为 $\mathcal{H} \left(\mathbf{x}\right)$，对于新的网络层我们不再拟合原始的映射关系，而是拟合 $\mathcal{F} \left(\mathbf{x}\right) = \mathcal{H} \left(\mathbf{x}\right) - \mathbf{x}$，也就是说原始潜在的映射关系变为 $\mathcal{F} \left(\mathbf{x}\right) + \mathbf{x}$。新的映射关系可以理解为在网络前向传播中添加了一条捷径 (shortcut connections)，如下图所示：

增加 Short Connections 并没有增加参数个数，也没有增加计算量，与此同时模型依旧可以利用 SGD 等算法进行优化。

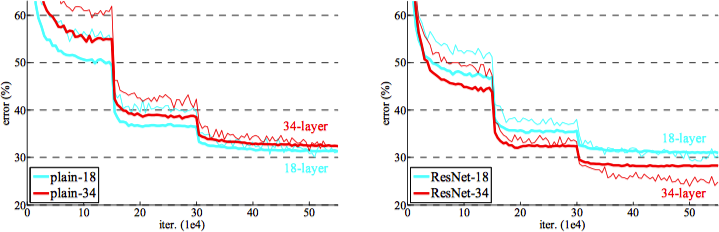
从 Deep Residual Net 的实验结果 (如上图) 可以看出，在没有加入残差模块的网络中 (上图 - 左) 出现了上文中描述的问题：更多层级的网络的效果反而较差；在加入了残差模块的网络中 (上图 - 右)，其整体性能均比未加入残差模块的网络要好，同时具有更多层级的网络的效果也更好。

随后 He 等人 ²⁰ 又提出了 Identity Mapping Residual Net，在原始的 ResNet 中，一个残差单元可以表示为：

$$ \begin{equation} \begin{split} \mathbb{y}_{\ell} = & h \left(\mathbb{x}_{\ell}\right) + \mathcal{F} \left(\mathbb{x}_{\ell}, \mathcal{W}_l\right) \\ \mathbb{x}_{\ell+1} = & f \left(\mathbb{y}_{\ell}\right) \end{split} \end{equation} $$

其中 $\mathbb{x}_{\ell}$ 和 $\mathbb{x}_{\ell+1}$ 为第 $\ell$ 个单元的输入和输出，$\mathcal{F}$ 为残差函数，$h \left(\mathbb{x}_{\ell}\right) = \mathbb{x}_{\ell}$ 为一个恒等映射，$f$ 为 ReLU 函数。在 Identity Mapping Residual Net，作者将 $f$ 由原来的 ReLU 函数也替换成一个恒定映射，即 $\mathbb{x}_{\ell+1} \equiv \mathbb{y}_{\ell}$，则上式可以改写为：

$$ \mathbb{x}_{\ell+1} = \mathbb{x}_{\ell} + \mathcal{F} \left(\mathbb{x}_{\ell}, \mathcal{W}_{\ell}\right) $$

则对于任意深度的单元 $L$，有如下表示：

$$ \mathbb{x}_L = \mathbb{x}_{\ell} + \sum_{i=\ell}^{L-1}{\mathcal{F} \left(\mathbb{x}_i, \mathcal{W}_i\right)} $$

上式形式的表示使得其在反向传播中具有一个很好的性质，假设损失函数为 $\mathcal{E}$，根据链式法则，对于单元 $\ell$，梯度为：

$$ \dfrac{\partial \mathcal{E}}{\partial \mathbb{x}_{\ell}} = \dfrac{\partial \mathcal{E}}{\partial \mathbb{x}_L} \dfrac{\partial \mathbb{x}_L}{\partial \mathbb{x}_{\ell}} = \dfrac{\partial \mathcal{E}}{\partial \mathbb{x}_{\ell}} \left(1 + \dfrac{\partial}{\partial \mathbb{x}_{\ell}} \sum_{i=\ell}^{L-1}{\mathcal{F} \left(\mathbb{x}_i, \mathcal{W}_i\right)}\right) $$

对于上式形式的梯度，我们可以将其拆解为两部分：$\frac{\partial \mathcal{E}}{\partial \mathbb{x}_{\ell}}$ 为不通过任何权重层的直接梯度传递，$\frac{\partial \mathcal{E}}{\partial \mathbb{x}_{\ell}} \left(\frac{\partial}{\partial \mathbb{x}_{\ell}} \sum_{i=\ell}^{L-1}{\mathcal{F} \left(\mathbb{x}_i, \mathcal{W}_i\right)}\right)$ 为通过权重层的梯度传递。前一项保证了梯度能够直接传回任意浅层 $\ell$，同时对于任意一个 mini-batch 的所有样本，$\frac{\partial}{\partial \mathbb{x}_{\ell}} \sum_{i=\ell}^{L-1}\mathcal{F}$ 不可能永远为 $-1$，所以保证了即使权重很小的情况下也不会出现梯度弥散。下图展示了原始的 ResNet 和 Identity Mapping Residual Net 之间残差单元的区别和网络的性能差异：

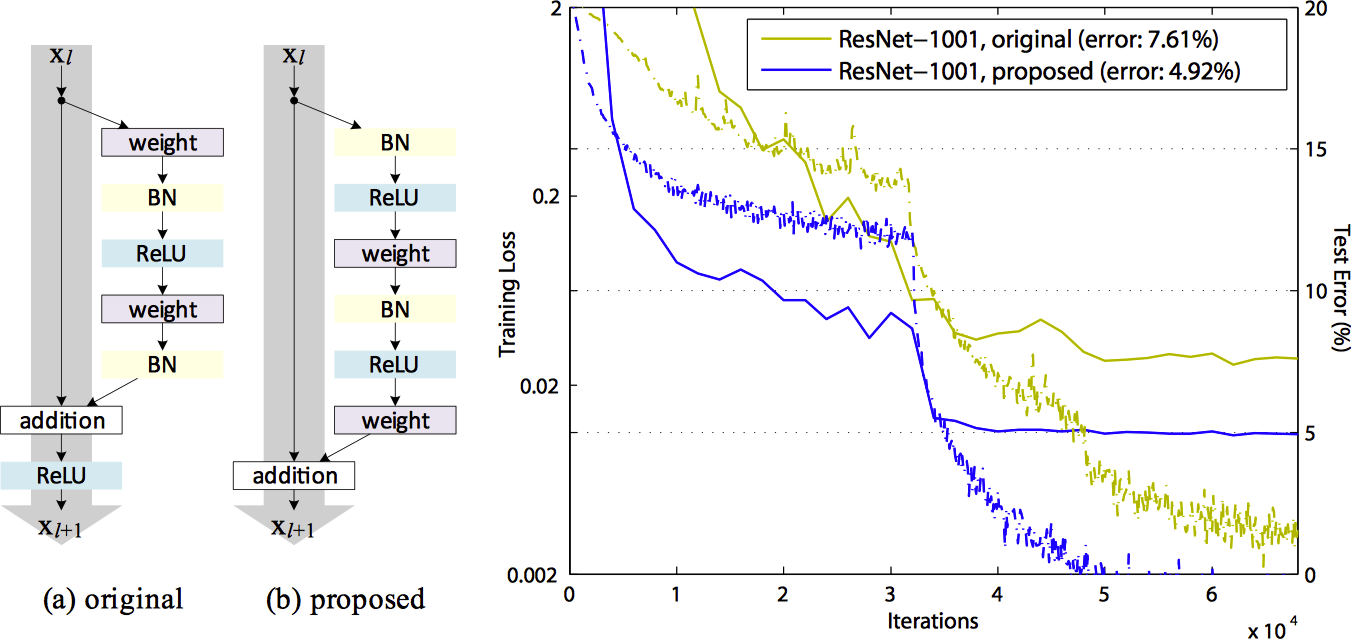
Huang 等人 ²¹ 在 ResNet 的基础上又提出了 DenseNet 网络，其网络结构如下所示：

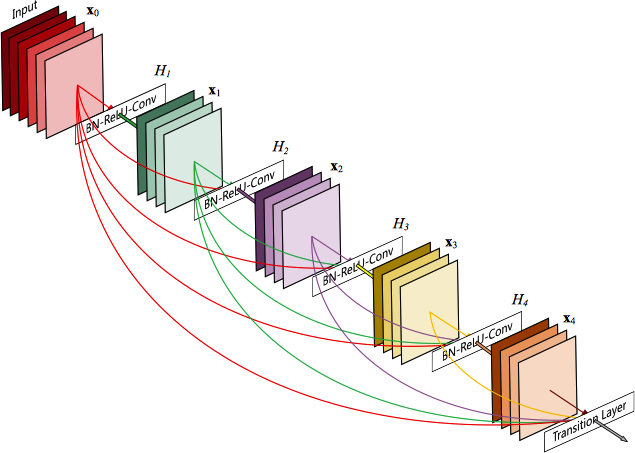
DenseNet 的主要改进如下：

• Dense Connectivity：将网络中每一层都与其后续层进行直接连接。
• Growth Rate：$H_{\ell}$ 将产生 $k$ 个 Feature Maps，因此第 $\ell$ 层将包含 $k_0 + k \times \left(\ell - 1\right)$ 个 Feature Maps，其中 $k_0$ 为输入层的通道数。DenseNet 与现有框架的不同之处就是将网络限定的比较窄，例如：$k = 12$，并将该超参数称之为网络的增长率 (Growth Rate)。
• Bottleneck Layers：在 3x3 的卷积之前增加 1x1 的卷积进行降维操作。
• Compression：在两个 Dense Block 之间增加过渡层 (Transition Layer)，进一步减少 Feature Maps 个数。

开源实现：

• tensorflow/models, tflearn/examples, tensorlayer/awesome-tensorlayer
• tf/keras/applications, keras/applications
• pytorch/torchvision/models
• caffe2/models
• incubator-mxnet/example

综合比较

Canziani 等人 ²² 综合了模型的准确率，参数大小，内存占用，推理时间等多个角度对现有的 CNN 模型进行了对比分析。

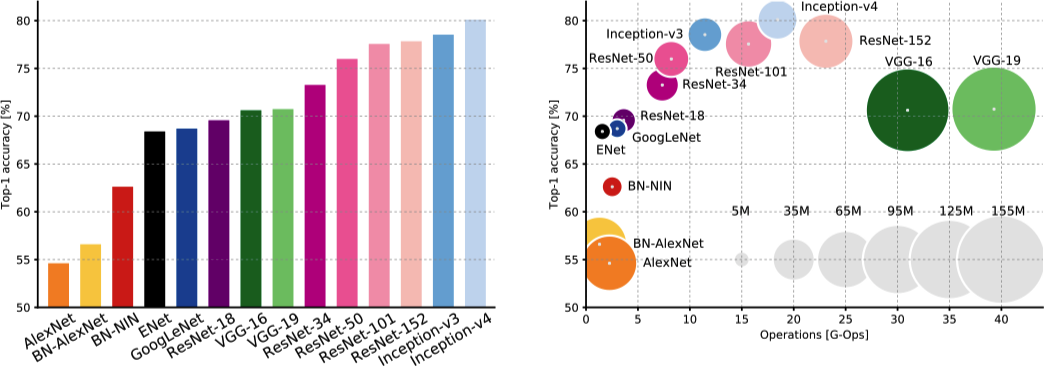
上图 (左) 展示了在 ImageNet 挑战赛中不同 CNN 网络模型的 Top-1 的准确率。可以看出近期的 ResNet 和 Inception 架构以至少 7% 的显著优势超过了其他架构。上图 (右) 以另一种形式展现了除了准确率以外的更多信息，包括计算成本和网络的参数个数，其中横轴为计算成本，纵轴为 Top-1 的准确率，气泡的大小为网络的参数个数。可以看出 ResNet 和 Inception 架构相比 AlexNet 和 VGG 不仅有更高的准确率，其在计算成本和网络的参数个数 (模型大小) 方面也具有一定优势。

文章部分内容参考了 刘昕 的 CNN近期进展与实用技巧。CNN 除了在图像分类问题上取得很大的进展外，在例如：物体检测：R-CNN ²³, SPP-Net ²⁴, Fast R-CNN ²⁵, Faster R-CNN ²⁶，语义分割：FCN ²⁷ 等多个领域也取得了不俗的成绩。针对不同的应用场景，网络模型和处理方法均有一定的差异，本文就不再对其他场景一一展开说明，不同场景将在后续进行单独整理。

「真诚赞赏，手留余香」

￥ 2 ￥ 5 ￥ 10 ￥ 50 ￥ 100 任意金额