文章部分内容参考了 Christopher 的博客 Understanding LSTM Networks,内容翻译和图片重绘已得到原作者同意。
发展史
循环神经网络 (Recurrent Neural Network, RNN) 一般是指时间递归神经网络而非结构递归神经网络 (Recursive Neural Network),其主要用于对序列数据进行建模。Salehinejad 等人 1 的一篇综述文章列举了 RNN 发展过程中的一些重大改进,如下表所示:
| Year | 1st Author | Contribution |
|---|---|---|
| 1990 | Elman | Popularized simple RNNs (Elman network) |
| 1993 | Doya | Teacher forcing for gradient descent (GD) |
| 1994 | Bengio | Difficulty in learning long term dependencies with gradient descend |
| 1997 | Hochreiter | LSTM: long-short term memory for vanishing gradients problem |
| 1997 | Schuster | BRNN: Bidirectional recurrent neural networks |
| 1998 | LeCun | Hessian matrix approach for vanishing gradients problem |
| 2000 | Gers | Extended LSTM with forget gates |
| 2001 | Goodman | Classes for fast Maximum entropy training |
| 2005 | Morin | A hierarchical softmax function for language modeling using RNNs |
| 2005 | Graves | BLSTM: Bidirectional LSTM |
| 2007 | Jaeger | Leaky integration neurons |
| 2007 | Graves | MDRNN: Multi-dimensional RNNs |
| 2009 | Graves | LSTM for hand-writing recognition |
| 2010 | Mikolov | RNN based language model |
| 2010 | Neir | Rectified linear unit (ReLU) for vanishing gradient problem |
| 2011 | Martens | Learning RNN with Hessian-free optimization |
| 2011 | Mikolov | RNN by back-propagation through time (BPTT) for statistical language modeling |
| 2011 | Sutskever | Hessian-free optimization with structural damping |
| 2011 | Duchi | Adaptive learning rates for each weight |
| 2012 | Gutmann | Noise-contrastive estimation (NCE) |
| 2012 | Mnih | NCE for training neural probabilistic language models (NPLMs) |
| 2012 | Pascanu | Avoiding exploding gradient problem by gradient clipping |
| 2013 | Mikolov | Negative sampling instead of hierarchical softmax |
| 2013 | Sutskever | Stochastic gradient descent (SGD) with momentum |
| 2013 | Graves | Deep LSTM RNNs (Stacked LSTM) |
| 2014 | Cho | Gated recurrent units |
| 2015 | Zaremba | Dropout for reducing Overfitting |
| 2015 | Mikolov | Structurally constrained recurrent network (SCRN) to enhance learning longer memory for vanishing gradient problem |
| 2015 | Visin | ReNet: A RNN-based alternative to convolutional neural networks |
| 2015 | Gregor | DRAW: Deep recurrent attentive writer |
| 2015 | Kalchbrenner | Grid long-short term memory |
| 2015 | Srivastava | Highway network |
| 2017 | Jing | Gated orthogonal recurrent units |
RNN
网络结构
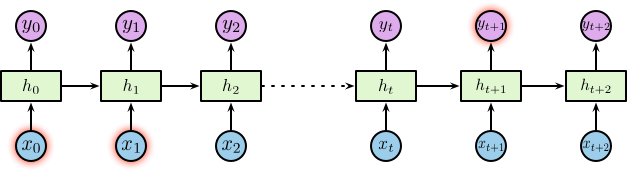
不同于传统的前馈神经网络接受特定的输入得到输出,RNN 由人工神经元和一个或多个反馈循环构成,如下图所示:
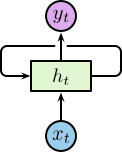
其中,$\boldsymbol{x}_t$ 为输入层,$\boldsymbol{h}_t$ 为带有循环的隐含层,$\boldsymbol{y}_t$ 为输出层。其中隐含层包含一个循环,为了便于理解我们将循环进行展开,展开后的网络结构如下图所示:
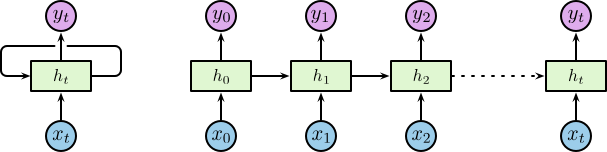
对于展开后的网络结构,其输入为一个时间序列 $\left\{\dotsc, \boldsymbol{x}_{t-1}, \boldsymbol{x}_t, \boldsymbol{x}_{t+1}, \dotsc\right\}$,其中 $\boldsymbol{x}_t \in \mathbb{R}^n$,$n$ 为输入层神经元个数。相应的隐含层为 $\left\{\dotsc, \boldsymbol{h}_{t-1}, \boldsymbol{h}_t, \boldsymbol{h}_{t+1}, \dotsc\right\}$,其中 $\boldsymbol{h}_t \in \mathbb{R}^m$,$m$ 为隐含层神经元个数。隐含层节点使用较小的非零数据进行初始化可以提升整体的性能和网络的稳定性 2。隐含层定义了整个系统的状态空间 (state space),或称之为 memory 1:
$$ \boldsymbol{h}_t = f_H \left(\boldsymbol{o}_t\right) $$
其中
$$ \boldsymbol{o}_t = \boldsymbol{W}_{IH} \boldsymbol{x}_t + \boldsymbol{W}_{HH} \boldsymbol{h}_{t-1} + \boldsymbol{b}_h $$
$f_H \left(\cdot\right)$ 为隐含层的激活函数,$\boldsymbol{b}_h$ 为隐含层的偏置向量。对应的输出层为 $\left\{\dotsc, \boldsymbol{y}_{t-1}, \boldsymbol{y}_t, \boldsymbol{y}_{t+1}, \dotsc\right\}$,其中 $\boldsymbol{y}_t \in \mathbb{R}^p$,$p$ 为输出层神经元个数。则:
$$ \boldsymbol{y}_t = f_O \left(\boldsymbol{W}_{HO} \boldsymbol{h}_t + \boldsymbol{b}_o\right) $$
其中 $f_O \left(\cdot\right)$ 为隐含层的激活函数,$\boldsymbol{b}_o$ 为隐含层的偏置向量。
在 RNN 中常用的激活函数为双曲正切函数:
$$ \tanh \left(x\right) = \dfrac{e^{2x} - 1}{e^{2x} + 1} $$
Tanh 函数实际上是 Sigmoid 函数的缩放:
$$ \sigma \left(x\right) = \dfrac{1}{1 + e^{-x}} = \dfrac{\tanh \left(x / 2\right) + 1}{2} $$
梯度弥散和梯度爆炸
原始 RNN 存在的严重的问题就是梯度弥散 (Vanishing Gradients) 和梯度爆炸 (Exploding Gradients)。我们以时间序列中的 3 个时间点 $t = 1, 2, 3$ 为例进行说明,首先假设神经元在前向传导过程中没有激活函数,则有:
$$ \begin{equation} \begin{split} &\boldsymbol{h}_1 = \boldsymbol{W}_{IH} \boldsymbol{x}_1 + \boldsymbol{W}_{HH} \boldsymbol{h}_0 + \boldsymbol{b}_h, &\boldsymbol{y}_1 = \boldsymbol{W}_{HO} \boldsymbol{h}_1 + \boldsymbol{b}_o \\ &\boldsymbol{h}_2 = \boldsymbol{W}_{IH} \boldsymbol{x}_2 + \boldsymbol{W}_{HH} \boldsymbol{h}_1 + \boldsymbol{b}_h, &\boldsymbol{y}_2 = \boldsymbol{W}_{HO} \boldsymbol{h}_2 + \boldsymbol{b}_o \\ &\boldsymbol{h}_3 = \boldsymbol{W}_{IH} \boldsymbol{x}_3 + \boldsymbol{W}_{HH} \boldsymbol{h}_2 + \boldsymbol{b}_h, &\boldsymbol{y}_3 = \boldsymbol{W}_{HO} \boldsymbol{h}_3 + \boldsymbol{b}_o \end{split} \end{equation} $$
在对于一个序列训练的损失函数为:
$$ \mathcal{L} \left(\boldsymbol{y}, \boldsymbol{\hat{y}}\right) = \sum_{t=0}^{T}{\mathcal{L}_t \left(\boldsymbol{y_t}, \boldsymbol{\hat{y}_t}\right)} $$
其中 $\mathcal{L}_t \left(\boldsymbol{y_t}, \boldsymbol{\hat{y}_t}\right)$ 为 $t$ 时刻的损失。我们利用 $t = 3$ 时刻的损失对 $\boldsymbol{W}_{IH}, \boldsymbol{W}_{HH}, \boldsymbol{W}_{HO}$ 求偏导,有:
$$ \begin{equation} \begin{split} \dfrac{\partial \mathcal{L}_3}{\partial \boldsymbol{W}_{HO}} &= \dfrac{\partial \mathcal{L}_3}{\partial \boldsymbol{y}_3} \dfrac{\partial \boldsymbol{y}_3}{\partial \boldsymbol{W}_{HO}} \\ \dfrac{\partial \mathcal{L}_3}{\partial \boldsymbol{W}_{IH}} &= \dfrac{\partial \mathcal{L}_3}{\partial \boldsymbol{y}_3} \dfrac{\partial \boldsymbol{y}_3}{\partial \boldsymbol{h}_3} \dfrac{\partial \boldsymbol{h}_3}{\partial \boldsymbol{W}_{IH}} + \dfrac{\partial \mathcal{L}_3}{\partial \boldsymbol{y}_3} \dfrac{\partial \boldsymbol{y}_3}{\partial \boldsymbol{h}_3} \dfrac{\partial \boldsymbol{h}_3}{\partial \boldsymbol{h}_2} \dfrac{\partial \boldsymbol{h}_2}{\partial \boldsymbol{W}_{IH}} + \dfrac{\partial \mathcal{L}_3}{\partial \boldsymbol{y}_3} \dfrac{\partial \boldsymbol{y}_3}{\partial \boldsymbol{h}_3} \dfrac{\partial \boldsymbol{h}_3}{\partial \boldsymbol{h}_2} \dfrac{\partial \boldsymbol{h}_2}{\partial \boldsymbol{h}_1} \dfrac{\partial \boldsymbol{h}_1}{\partial \boldsymbol{W}_{IH}} \\ \dfrac{\partial \mathcal{L}_3}{\partial \boldsymbol{W}_{HH}} &= \dfrac{\partial \mathcal{L}_3}{\partial \boldsymbol{y}_3} \dfrac{\partial \boldsymbol{y}_3}{\partial \boldsymbol{h}_3} \dfrac{\partial \boldsymbol{h}_3}{\partial \boldsymbol{W}_{HH}} + \dfrac{\partial \mathcal{L}_3}{\partial \boldsymbol{y}_3} \dfrac{\partial \boldsymbol{y}_3}{\partial \boldsymbol{h}_3} \dfrac{\partial \boldsymbol{h}_3}{\partial \boldsymbol{h}_2} \dfrac{\partial \boldsymbol{h}_2}{\partial \boldsymbol{W}_{HH}} + \dfrac{\partial \mathcal{L}_3}{\partial \boldsymbol{y}_3} \dfrac{\partial \boldsymbol{y}_3}{\partial \boldsymbol{h}_3} \dfrac{\partial \boldsymbol{h}_3}{\partial \boldsymbol{h}_2} \dfrac{\partial \boldsymbol{h}_2}{\partial \boldsymbol{h}_1} \dfrac{\partial \boldsymbol{h}_1}{\partial \boldsymbol{W}_{HH}} \end{split} \end{equation} $$
因此,不难得出对于任意时刻 $t$,$\boldsymbol{W}_{IH}, \boldsymbol{W}_{HH}$ 的偏导为:
$$ \dfrac{\partial \mathcal{L}_t}{\partial \boldsymbol{W}_{IH}} = \sum_{k=0}^{t}{\dfrac{\partial \mathcal{L}_t}{\partial \boldsymbol{y}_t} \dfrac{\partial \boldsymbol{y}_t}{\partial \boldsymbol{h}_t} \left(\prod_{j=k+1}^{t}{\dfrac{\partial \boldsymbol{h}_j}{\partial \boldsymbol{h}_{j-1}}}\right) \dfrac{\partial \boldsymbol{h}_k}{\partial \boldsymbol{W}_{IH}}} $$
$\dfrac{\partial \mathcal{L}_t}{\partial \boldsymbol{W}_{HH}}$ 同理可得。对于 $\dfrac{\partial \mathcal{L}_t}{\partial \boldsymbol{W}_{HH}}$,在存在激活函数的情况下,有:
$$ \prod_{j=k+1}^{t}{\dfrac{\partial \boldsymbol{h}_j}{\partial \boldsymbol{h}_{j-1}}} = \prod_{j=k+1}^{t}{f'_H \left(h_{j-1}\right) \boldsymbol{W}_{HH}} $$
假设激活函数为 $\tanh$,下图刻画了 $\tanh$ 函数及其导数的函数取值范围:
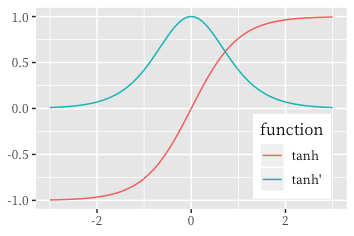
可得,$0 \leq \tanh' \leq 1$,同时当且仅当 $x = 0$ 时,$\tanh' \left(x\right) = 1$。因此:
- 当
$t$较大时,$\prod_{j=k+1}^{t}{f'_H \left(h_{j-1}\right) \boldsymbol{W}_{HH}}$趋近于 0,则会产生梯度弥散问题。 - 当
$\boldsymbol{W}_{HH}$较大时,$\prod_{j=k+1}^{t}{f'_H \left(h_{j-1}\right) \boldsymbol{W}_{HH}}$趋近于无穷,则会产生梯度爆炸问题。
长期依赖问题
RNN 隐藏节点以循环结构形成记忆,每一时刻的隐藏层的状态取决于它的过去状态,这种结构使得 RNN 可以保存、记住和处理长时期的过去复杂信号。但有的时候,我们仅需利用最近的信息来处理当前的任务。例如:考虑一个用于利用之前的文字预测后续文字的语言模型,如果我们想预测 “the clouds are in the sky” 中的最后一个词,我们不需要太远的上下信息,很显然这个词就应该是 sky。在这个情况下,待预测位置与相关的信息之间的间隔较小,RNN 可以有效的利用过去的信息。
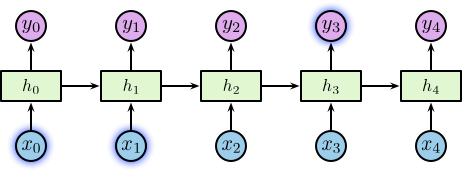
但也有很多的情况需要更多的上下文信息,考虑需要预测的文本为 “I grew up in France … I speak fluent French”。较近的信息表明待预测的位置应该是一种语言,但想确定具体是哪种语言需要更远位置的“在法国长大”的背景信息。理论上 RNN 有能力处理这种长期依赖,但在实践中 RNN 却很难解决这个问题 3。
LSTM
LSTM 网络结构
长短时记忆网络 (Long Short Term Memroy, LSTM) 是由 Hochreiter 和 Schmidhuber 4 提出一种特殊的 RNN。LSTM 的目的就是为了解决长期依赖问题,记住长时间的信息是 LSTM 的基本功能。
所有的循环神经网络都是由重复的模块构成的一个链条。在标准的 RNN 中,这个重复的模块的结构比较简单,仅包含一个激活函数为 $\tanh$ 的隐含层,如下图所示:
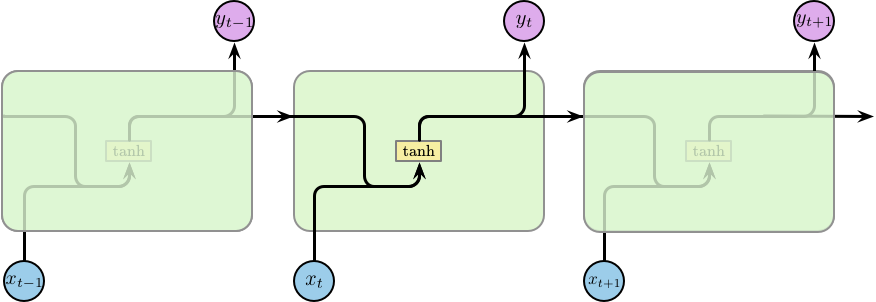
LSTM 也是类似的链条状结构,但其重复的模块的内部结构不同。模块内部并不是一个隐含层,而是四个,并且以一种特殊的方式进行交互,如下图所示:
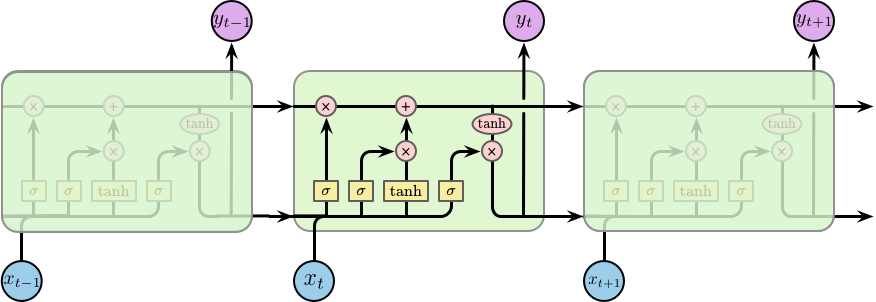
下面我们将一步一步的介绍 LSTM 单元 (cell) 的具体工作原理,在之前我们先对使用到的符号进行简单的说明,如下图所示:

其中,每条线都包含一个从输出节点到其他节点的整个向量,粉红色的圆圈表示逐元素的操作,黄色的矩形为学习到的神经网络层,线条的合并表示连接,线条的分叉表示内容的复制并转移到不同位置。
LSTM 单元状态和门控机制
LSTM 的关键为单元的状态 (cell state),即下图中顶部水平穿过单元的直线。单元的状态像是一条传送带,其直接运行在整个链条上,同时仅包含少量的线性操作。因此,信息可以很容易得传递下去并保持不变。
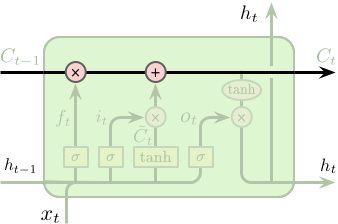
LSTM 具有向单元状态添加或删除信息的能力,这种能力被由一种称之为“门” (gates) 的结构所控制。门是一种可选择性的让信息通过的组件,其由一层以 Sigmoid 为激活函数的网络层和一个逐元素相乘操作构成的,如下图所示:

Sigmoid 层的输出值介于 0 和 1 之间,代表了所允许通过的数据量。0 表示不允许任何数据通过,1 表示允许所有数据通过。一个 LSTM 单元包含 3 个门用于控制单元的状态。
LSTM 工作步骤
LSTM 的第一步是要决定从单元状态中所忘记的信息,这一步是通过一个称之为“遗忘门 (forget gate)”的 Sigmoid 网络层控制。该层以上一时刻隐含层的输出 $h_{t-1}$ 和当前这个时刻的输入 $x_t$ 作为输入,输出为一个介于 0 和 1 之间的值,1 代表全部保留,0 代表全部丢弃。回到之前的语言模型,单元状态需要包含主语的性别信息以便选择正确的代词。但当遇见一个新的主语后,则需要忘记之前主语的性别信息。
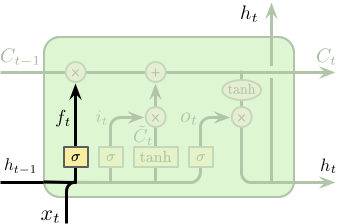
$$ f_t = \sigma \left(W_f \cdot \left[h_{t-1}, x_t\right] + b_f\right) $$
第二步我们需要决定要在单元状态中存储什么样的新信息,这包含两个部分。第一部分为一个称之为“输入门 (input gate)” 的 Sigmoid 网络层,其决定更新那些数据。第二部分为一个 Tanh 网络层,其将产生一个新的候选值向量 $\tilde{C}_t$ 并用于添加到单元状态中。之后会将两者进行整合,并对单元状态进行更新。在我们的语言模型中,我们希望将新主语的性别信息添加到单元状态中并替代需要忘记的旧主语的性别信息。
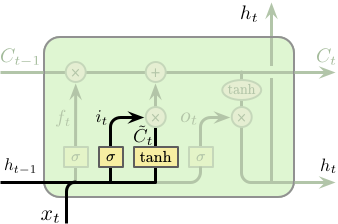
$$ \begin{equation} \begin{split} i_t &= \sigma \left(W_i \cdot \left[h_{t-1}, x_t\right] + b_i\right) \\ \tilde{C}_t &= \tanh \left(W_C \cdot \left[h_{t-1}, x_t\right] + b_C\right) \end{split} \end{equation} $$
接下来需要将旧的单元状态 $C_{t-1}$ 更新为 $C_t$。我们将旧的单元状态乘以 $f_t$ 以控制需要忘记多少之前旧的信息,再加上 $i_t \odot \tilde{C}_t$ 用于控制单元状态的更新。在我们的语言模型中,该操作真正实现了我们对与之前主语性别信息的遗忘和对新信息的增加。
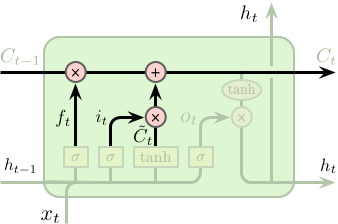
$$ C_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_t $$
最后我们需要确定单元的输出,该输出将基于单元的状态,但为一个过滤版本。首先我们利用一个 Sigmoid 网络层来确定单元状态的输出,其次我们对单元状态进行 $\tanh$ 操作 (将其值缩放到 -1 和 1 之间) 并与之前 Sigmoid 层的输出相乘,最终得到需要输出的信息。
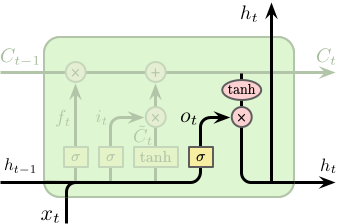
$$ \begin{equation} \begin{split} o_t &= \sigma \left(W_o \cdot \left[h_{t-1}, x_t\right] + b_o\right) \\ h_t &= o_t \odot \tanh \left(C_t\right) \end{split} \end{equation} $$
LSTM 变种
上文中介绍的基础的 LSTM 模型,事实上不同学者对 LSTM 的结构进行了或多或少的改变,其中一个比较有名的变种是由 Gers 和 Schmidhuber 提出的 5。其添加了一种“窥视孔连接 (peephole connections)”,这使得每一个门结构都能够窥视到单元的状态。
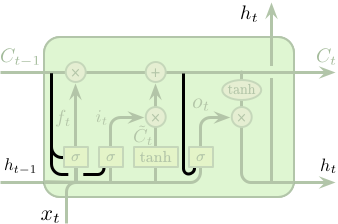
$$ \begin{equation} \begin{split} f_t &= \sigma \left(W_f \cdot \left[\boldsymbol{C_{t-1}}, h_{t-1}, x_t\right] + b_f\right) \\ i_t &= \sigma \left(W_i \cdot \left[\boldsymbol{C_{t-1}}, h_{t-1}, x_t\right] + b_i\right) \\ o_t &= \sigma \left(W_o \cdot \left[\boldsymbol{C_t}, h_{t-1}, x_t\right] + b_o\right) \end{split} \end{equation} $$
另一个变种是使用了成对的遗忘门和输入门。不同于一般的 LSTM 中分别确定需要遗忘和新添加的信息,成对的遗忘门和输入门仅在需要添加新输入是才会忘记部分信息,同理仅在需要忘记信息时才会添加新的输入。
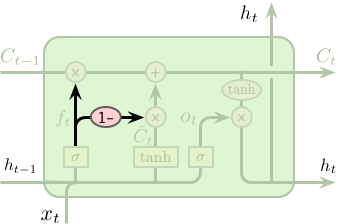
$$ C_t = f_t \odot C_{t-1} + \boldsymbol{\left(1 - f_t\right)} \odot \tilde{C}_t $$
另外一个比较有名的变种为 Cho 等人提出的 Gated Recurrent Unit (GRU) 6,单元结构如下:
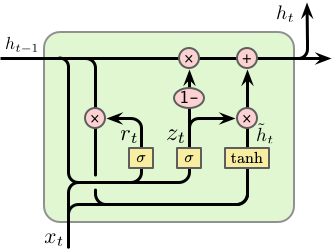
GRU 将遗忘门和输入门整个成一层,称之为“更新门 (update gate)”,同时配以一个“重置门 (reset gate)”。具体的计算过程如下:
首先计算更新门 $z_t$ 和重置门 $r_t$:
$$ \begin{equation} \begin{split} z_t &= \sigma \left(W_z \cdot \left[h_{t-1}, x_t\right]\right) \\ r_t &= \sigma \left(W_r \cdot \left[h_{t-1}, x_t\right]\right) \end{split} \end{equation} $$
其次计算候选隐含层 (candidate hidden layer) $\tilde{h}_t$,与 LSTM 中计算 $\tilde{C}_t$ 类似,其中 $r_t$ 用于控制保留多少之前的信息:
$$ \tilde{h}_t = \tanh \left(W \cdot \left[r_t \odot h_{t-1}, x_t\right]\right) $$
最后计算需要从之前的隐含层 $h_{t-1}$ 遗忘多少信息,同时加入多少新的信息 $\tilde{h}_t$,$z_t$ 用于控制这个比例:
$$ h_t = \left(1 - z_t\right) \odot h_{t-1} + z_t \odot \tilde{h}_t $$
因此,对于短距离依赖的单元重置门的值较大,对于长距离依赖的单元更新门的值较大。如果 $r_t = 1$ 并且 $z_t = 0$,则 GRU 退化为一个标准的 RNN。
除此之外还有大量的 LSTM 变种,Greff 等人 7 对一些常见的变种进行了比较,Jozefowicz 等人 8 测试了大量的 RNN 结构在不同任务上的表现。
扩展与应用
循环神经网络在序列建模上有着天然的优势,其在自然语言处理,包括:语言建模,语音识别,机器翻译,对话与QA,文本生成等;计算视觉,包括:目标识别,视觉追踪,图像生成等;以及一些综合场景,包括:图像标题生成,视频字幕生成等,多个领域均有不错的表现,有代表性的论文请参见 awesome-rnn。
Google 的 Magenta 是一项利用机器学习创作艺术和音乐的研究,其中也包含了大量利用 RNN 相关模型构建的有趣项目。SketchRNN 是由 Ha 等人 9 提出了一种能够根据用户描绘的一些简单图形自动完成后续绘画的 RNN 网络。

Performance RNN 是由 Ian 等人 10 提出了一种基于时间和动态因素生成复合音乐的 LSTM 网络。
更多有趣的作品请参见 Megenta 的 Demos 页面。
-
Salehinejad, H., Sankar, S., Barfett, J., Colak, E., & Valaee, S. (2017). Recent Advances in Recurrent Neural Networks. arXiv preprint arXiv:1801.01078. ↩︎ ↩︎
-
Sutskever, I., Martens, J., Dahl, G., & Hinton, G. (2013). On the importance of initialization and momentum in deep learning. In International Conference on Machine Learning (pp. 1139–1147). ↩︎
-
Bengio, Y., Simard, P., & Frasconi, P. (1994). Learning long-term dependencies with gradient descent is difficult. IEEE Transactions on Neural Networks, 5(2), 157–166. ↩︎
-
Hochreiter, S., & Schmidhuber, J. (1997). Long short-term memory. Neural Computation, 9(8), 1735–1780. ↩︎
-
Gers, F. A., & Schmidhuber, J. (2000). Recurrent nets that time and count. In Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks. IJCNN 2000. Neural Computing: New Challenges and Perspectives for the New Millennium (Vol. 3, pp. 189–194 vol.3). ↩︎
-
Cho, K., van Merrienboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., & Bengio, Y. (2014). Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP) (pp. 1724–1734). ↩︎
-
Greff, K., Srivastava, R. K., Koutník, J., Steunebrink, B. R., & Schmidhuber, J. (2017). LSTM: A Search Space Odyssey. IEEE Transactions on Neural Networks and Learning Systems, 28(10), 2222–2232. ↩︎
-
Jozefowicz, R., Zaremba, W., & Sutskever, I. (2015). An Empirical Exploration of Recurrent Network Architectures. In Proceedings of the 32Nd International Conference on International Conference on Machine Learning - Volume 37 (pp. 2342–2350). ↩︎
-
Ha, D., & Eck, D. (2017). A Neural Representation of Sketch Drawings. arXiv preprint arXiv:1704.03477 ↩︎
-
Ian S., & Sageev O. Performance RNN: Generating Music with Expressive Timing and Dynamics. Magenta Blog, 2017. https://magenta.tensorflow.org/performance-rnn ↩︎