贝塞尔曲线 (Bézier Curve)
范叶亮 / 2019-02-19
分类: 数学, 可视化 / 标签: 贝塞尔曲线, Bézier Curve / 字数: 1207
知道贝塞尔曲线 (Bézier Curve) 这个名字已经有很长一段时间了，但一直没有去详细了解一番。直到最近想要绘制一个比较复杂的曲线，才发现很多工具都以贝塞尔曲线为基础的，这包括 Adobe 全家桶中的钢笔工具，还有 OmniGraffle 中的曲线。迫于仅靠猜其是如何工作的但一直没猜透的无奈，只能去详细了解一下其原理再使用了。
数学表示
贝塞尔曲线 (Bézier Curve) 是由法国工程师皮埃尔·贝兹 (Pierre Bézier) 于 1962 年所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计 1。贝塞尔曲线最初由保尔·德·卡斯特里奥 (Paul de Casteljau) 于 1959 年运用德卡斯特里奥算法 (De Casteljau’s Algorithm) 开发，以稳定数值的方法求出贝塞尔曲线。
线性贝塞尔曲线
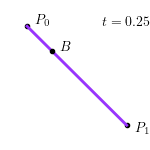
给定点 $P_0, P_1$，线性贝塞尔曲线定义为：
$$ B \left(t\right) = \left(1 - t\right) P_0 + t P_1, t \in \left[0, 1\right] $$
不难看出，线性贝塞尔曲线即为点 $P_0$ 和 $P_1$ 之间的线段。
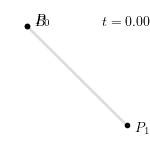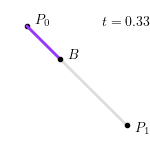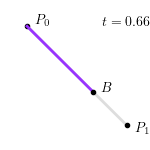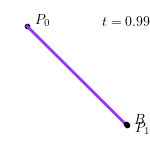
对于 $P_0 = \left(4, 6\right), P_1 = \left(10, 0\right)$，当 $t = 0.25$ 时，线性贝塞尔曲线如下图所示：
整个线性贝塞尔曲线生成过程如下图所示：
二次贝塞尔曲线
给定点 $P_0, P_1, P_2$，二次贝塞尔曲线定义为：
$$ B \left(t\right) = \left(1 - t\right)^2 P_0 + 2 t \left(1 - t\right) P_1 + t^2 P_2, t \in \left[0, 1\right] $$
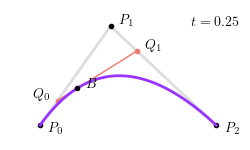
对于 $P_0 = \left(0, 0\right), P_1 = \left(4, 6\right), P_2 = \left(10, 0\right)$，当 $t = 0.25$ 时，二次贝塞尔曲线如下图所示：
整个二次贝塞尔曲线生成过程如下图所示：
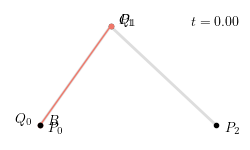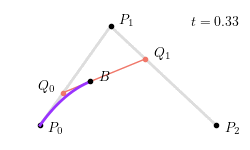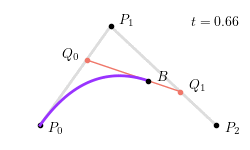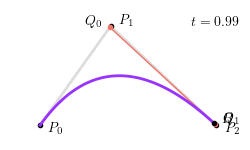
三次贝塞尔曲线
给定点 $P_0, P_1, P_2, P_3$，三次贝塞尔曲线定义为：
$$ B \left(t\right) = \left(1 - t\right)^3 P_0 + 3 t \left(1 - t\right)^2 P_1 + 3 t^2 \left(1 - t\right) P_2 + t^3 P_3, t \in \left[0, 1\right] $$
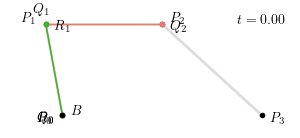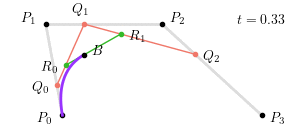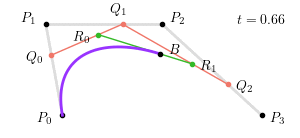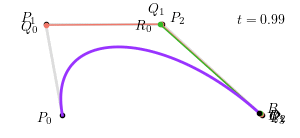
对于 $P_0 = \left(0, 0\right), P_1 = \left(-1, 6\right), P_2 = \left(6, 6\right), P_3 = \left(12, 0\right)$，当 $t = 0.25$ 时，三次贝塞尔曲线如下图所示：
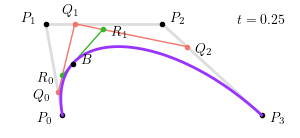
整个三次贝塞尔曲线生成过程如下图所示：
一般化的贝塞尔曲线
对于一般化的贝塞尔曲线，给定点 $P_0, P_1, \cdots, P_n$， $n$ 次贝塞尔曲线定义为：
$$ B \left(t\right) = \sum_{i=0}^{n}{\binom{n}{i} \left(1 - t\right)^{n - i} t^{i} P_i}, t \in \left[0, 1\right] $$
其中，
$$ b_{i, n} \left(t\right) = \binom{n}{i} \left(1 - t\right)^{n - i} t^{i} $$
称之为 $n$ 阶 Bernstein 多项式，点 $P_i$ 称为贝塞尔曲线的控制点。从生成过程来看，贝塞尔曲线是通过 $n$ 次中介点 ($Q_j, R_k, S_l$) 生成的，一个更加复杂的四次贝塞尔曲线 ($t = 0.25$) 如下图所示：
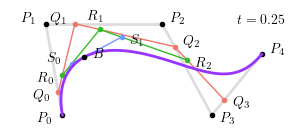
整个四次贝塞尔曲线生成过程如下图所示：
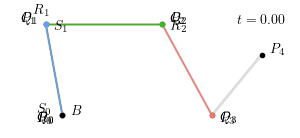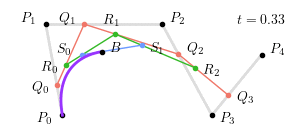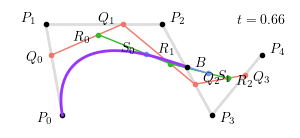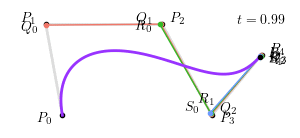
其中，$Q_0 = \left(1 - t\right) P_0 + t P_1$，$R_0 = \left(1 - t\right) Q_0 + t Q_1$，$S_0 = \left(1 - t\right) R_0 + t R_1$，$B = \left(1 - t\right) S_0 + t S_1$ 为构成贝塞尔曲线的点。
上述图形和动画的绘制代码请参见这里。
应用技巧
在很多绘图软件中，钢笔工具使用的是三次贝塞尔曲线，其中起始点和结束点分别对应 $P_0$ 和 $P_1$，起始点和结束点的控制点分别对应 $P_2$ 和 $P_3$。
在利用钢笔工具绘图时，可以参考如下建议来快速高效地完成绘图 2：
- 控制点尽可能在曲线的最外侧或最内侧。
- 除了曲线的结束处外，控制点的控制柄尽可能水平或垂直。
- 合理安排控制点的密度。
下面两张图分别展示了一个原始的字母图案，以及参考上述建议利用贝塞尔曲线勾勒出来的字母图案边框：
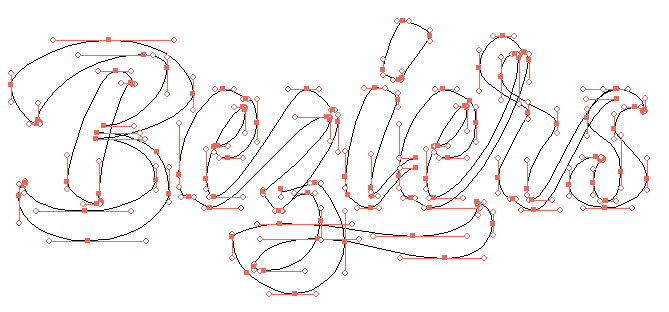
最后推荐一个网站 The Bezier Game，可以帮助更好的理解和掌握基于贝塞尔曲线的钢笔工具使用。