准备知识

向量与基

$\renewcommand{\diag}{\operatorname{diag}}\renewcommand{\cov}{\operatorname{cov}}$首先，定义 $\boldsymbol{\alpha}$ 为列向量，则维度相同的两个向量 $\boldsymbol{\alpha}, \boldsymbol{\beta}$ 的内积可以表示为：

$$\boldsymbol{\alpha} \cdot \boldsymbol{\beta} = \boldsymbol{\alpha}^T \boldsymbol{\beta} = \sum_{i=1}^{n}{\alpha_i b_i}$$

后续为了便于理解，我们以二维向量为例，则 $\boldsymbol{\alpha} = \left(x_1, y_1\right)^T, \boldsymbol{\beta} = \left(x_2, y_2\right)^T$，在直角座标系中可以两个向量表示如下：

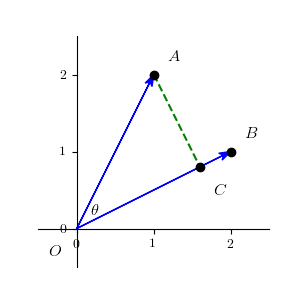
我们从 $A$ 点向向量 $\boldsymbol{\beta}$ 的方向做一条垂线，交于点 $C$，则称 $OC$ 为 $OA$ 在 $OB$ 方向上的投影。设向量 $\boldsymbol{\alpha}$ 和向量 $\boldsymbol{\beta}$ 的夹角为 $\theta$，则：

$$\cos \left(\theta\right) = \dfrac{\boldsymbol{\alpha} \cdot \boldsymbol{\beta}}{\lvert\boldsymbol{\alpha}\rvert \lvert\boldsymbol{\beta}\rvert}$$

其中，$\lvert\boldsymbol{\alpha}\rvert = \sqrt{x_1^2 + y_1^2}$，则 $OC$ 的长度为 $\lvert\boldsymbol{\alpha}\rvert \cos\left(\theta\right)$。

在 $n$ 维的线性空间 $V$ 中，$n$ 个线性无关的向量 $\boldsymbol{\epsilon_1, \epsilon_2, ..., \epsilon_n}$ 称为 $V$ 的一组基。则对于 $V$ 中的任一向量 $\boldsymbol{\alpha}$ 可以由这组基线性表示出来：

$$\boldsymbol{\alpha} = x_1 \boldsymbol{\epsilon_1} + x_2 \boldsymbol{\epsilon_2} + ... + x_n \boldsymbol{\epsilon_n}$$

则对于向量 $\boldsymbol{\alpha} = \left(3, 2\right)^T$，可以表示为：

$$\boldsymbol{\alpha} = 3 \left(1, 0\right)^T + 2 \left(0, 1\right)^T$$

其中 $\left(1, 0\right)^T$ 和 $\left(0, 1\right)^T$ 为二维空间中的一组基。

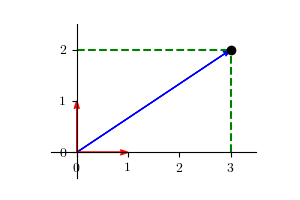
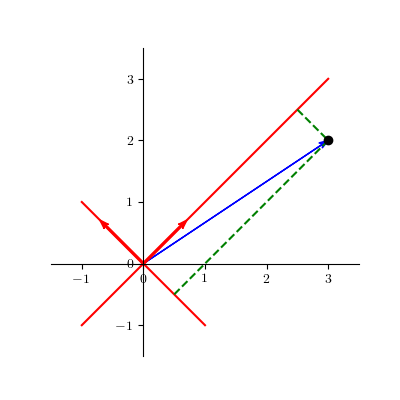
因此，当我们确定好一组基之后，我们仅需利用向量在基上的投影值即可表示对应的向量。一般情况下，我们会选择由坐标轴方向上的单位向量构成的基作为默认的基来表示向量，但我们仍可选择其他的基。例如，我们选择 $\left(-\dfrac{1}{\sqrt{2}}, \dfrac{1}{\sqrt{2}}\right)$ 和 $\left(\dfrac{1}{\sqrt{2}}, \dfrac{1}{\sqrt{2}}\right)$ 作为一组基，则向量在这组基上的坐标为 $\left(-\dfrac{1}{\sqrt{2}}, \dfrac{5}{\sqrt{2}}\right)$，示例如下：

线性变换

以二维空间为例，定义一个如下矩阵

$$ A = \left\lgroup \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right\rgroup $$

则对于二维空间中一个向量 $\boldsymbol{\alpha} = \left(x, y\right)^T$ ，通过同上述矩阵进行乘法运算，可得

$$ \boldsymbol{\alpha'} = A \boldsymbol{\alpha} = \left\lgroup \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right\rgroup \left\lgroup \begin{array}{c} x \\ y \end{array} \right\rgroup = \left\lgroup \begin{array}{c} x' \\ y' \end{array} \right\rgroup $$

(1) 通过变换将任意一个点 $x$ 变成它关于 $x$ 轴对称的点 $x'$

$$ x' = \left\lgroup \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right\rgroup \left\lgroup \begin{array}{c} x \\ y \end{array} \right\rgroup = \left\lgroup \begin{array}{c} x \\ -y \end{array} \right\rgroup $$

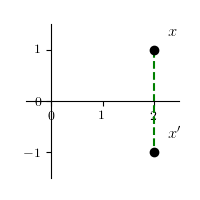
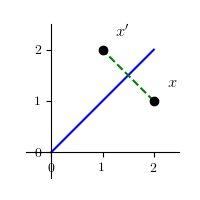
(2) 通过变换将任意一个点 $x$ 变成它关于 $y = x$ 对称的点 $x'$

$$ x' = \left\lgroup \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right\rgroup \left\lgroup \begin{array}{c} x \\ y \end{array} \right\rgroup = \left\lgroup \begin{array}{c} y \\ x \end{array} \right\rgroup $$

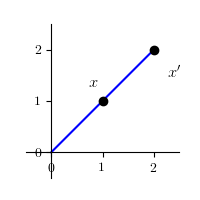
(3) 变换将任意一个点 $x$ 变成在它与原点连线上，与原点距离伸缩为 $|\lambda|$ 倍的点 $x'$

$$ x' = \left\lgroup \begin{array}{cc} \lambda & 0 \\ 0 & \lambda \end{array} \right\rgroup \left\lgroup \begin{array}{c} x \\ y \end{array} \right\rgroup = \left\lgroup \begin{array}{c} \lambda x \\ \lambda y \end{array} \right\rgroup $$

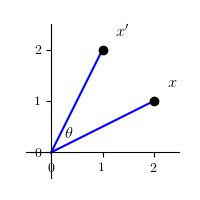
(4) 通过变换将任意一个点 $x$ 绕原点旋转了角度 $\theta$ 的点 $x'$

$$ \begin{equation} \begin{split} x'& = \left\lgroup \begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array} \right\rgroup \left\lgroup \begin{array}{c} x \\ y \end{array} \right\rgroup \\ & = \left\lgroup \begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array} \right\rgroup \left\lgroup \begin{array}{c} r \cos \phi \\ r \sin \phi \end{array} \right\rgroup \\ & = \left\lgroup \begin{array}{c} r \cos \left(\phi + \theta\right) \\ r \sin \left(\phi + \theta\right) \end{array} \right\rgroup \end{split} \end{equation} $$

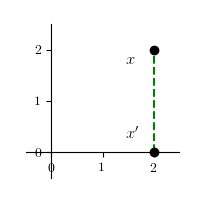
(5) 变换将任意一个点 $x$ 变成它在 $x$ 轴上 的投影点 $x'$

$$ x' = \left\lgroup \begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array} \right\rgroup \left\lgroup \begin{array}{c} x \\ y \end{array} \right\rgroup = \left\lgroup \begin{array}{c} x \\ 0 \end{array} \right\rgroup $$

特征值分解

设 $A$ 是线性空间 $V$ 上的一个线性变换，对于一个非零向量 $\boldsymbol{\alpha} = \left(x_1, x_2, ..., x_n\right)^T$ 使得

$$A \boldsymbol{\alpha} = \lambda \boldsymbol{\alpha}$$

则 $\lambda$ 称为 $A$ 的一个特征值，$\boldsymbol{\alpha}$ 称为 $A$ 的一个特征向量。通过

$$ \begin{equation} \begin{split} A \boldsymbol{\alpha} &= \lambda \boldsymbol{\alpha} \\ A \boldsymbol{\alpha} - \lambda \boldsymbol{\alpha} &= 0 \\ \left(A - \lambda E\right) \boldsymbol{\alpha} &= 0 \\ A - \lambda E &= 0 \end{split} \end{equation} $$

其中 $E = \diag \left(1, 1, ..., 1\right)$ 为单位对角阵，即可求解其特征值，进而求解特征向量。若 $A$ 是一个可逆矩阵，则上式可以改写为：

$$ A = Q \sum Q^{-1} $$

这样，一个方阵 $A$ 就被一组特征值和特征向量表示了。例如，对于如下矩阵进行特征值分解

$$ A = \left\lgroup \begin{array}{cccc} 3 & -2 & -0.9 & 0 \\ -2 & 4 & 1 & 0 \\ 0 & 0 & -1 & 0 \\ -0.5 & -0.5 & 0.1 & 1 \end{array} \right\rgroup $$

A <- matrix(c(3, -2, -0.9, 0,
              -2, 4, 1, 0,
              0, 0, -1, 0,
              -0.5, -0.5, 0.1, 1),
            4, 4, byrow = T)
A_eig <- eigen(A)
print(A_eig)

# eigen() decomposition
# $values
# [1]  5.561553  1.438447  1.000000 -1.000000
# 
# $vectors
#             [,1]       [,2] [,3]        [,4]
# [1,] -0.61530186  0.4176225    0  0.15282144
# [2,]  0.78806410  0.3260698    0 -0.13448286
# [3,]  0.00000000  0.0000000    0  0.97805719
# [4,] -0.01893678 -0.8480979    1 -0.04431822

则利用特征值和特征向量，可以还原原矩阵

A_re <- A_eig$vectors %*%
    diag(A_eig$values) %*%
    solve(A_eig$vectors)
print(A_re)

#      [,1] [,2] [,3] [,4]
# [1,]  3.0 -2.0 -0.9    0
# [2,] -2.0  4.0  1.0    0
# [3,]  0.0  0.0 -1.0    0
# [4,] -0.5 -0.5  0.1    1

奇异值分解

特征值分解针对的是方阵，对于一个 $m*n$ 的矩阵是无法进行特征值分解的，这时我们就需要使用奇异值分解来解决这个问题。对于 $m*n$ 的矩阵 $A$，可得 $A A^T$ 是一个 $m*m$ 的方阵，则针对 $A A^T$，通过 $\left(A A^T\right) \boldsymbol{\alpha} = \lambda \boldsymbol{\alpha}$，即可求解这个方阵的特征值和特征向量。针对矩阵 $A$，奇异值分解是将原矩阵分解为三个部分

$$ A_{m*n} = U_{m*r} \sum\nolimits_{r*r} V_{r*n}^T $$

其中 $U$ 称之为左奇异向量，即为 $A A^T$ 单位化后的特征向量；$V$ 称之为右奇异向量，即为 $A^T A$ 单位化后的特征向量；$\sum$矩阵对角线上的值称之为奇异值，即为 $A A^T$ 或 $A^T A$ 特征值的平方根。

我们利用经典的 lena 图片展示一下 SVD 的作用，lena图片为一张 $512*512$ 像素的彩色图片

我们对原始图片进行灰度处理后，进行特征值分解，下图中从左到右，从上到下分别是原始的灰度图像，利用 20 个左奇异向量和 20 个右奇异向量重构图像，利用 50 个左奇异向量和 100 个右奇异向量重构图像，利用 200 个左奇异向量和 200 个右奇异向量重构图像。

从图中可以看出，我们仅用了 200 个左奇异向量和 200 个右奇异向量重构图像与原始灰度图像已经基本看不出任何区别。因此，我们利用 SVD 可以通过仅保留较大的奇异值实现数据的压缩。

主成分分析

主成分分析¹可以通俗的理解为一种降维方法。其目标可以理解为将一个 $m$ 维的数据转换称一个 $k$ 维的数据，其中 $k < m$。对于具有 $n$ 个样本的数据集，设 $\boldsymbol{x_i}$ 表示 $m$ 维的列向量，则

$$ X_{m*n} = \left(\boldsymbol{x_1}, \boldsymbol{x_2}, ..., \boldsymbol{x_n}\right) $$

对每一个维度进行零均值化，即减去这一维度的均值

$$ X'_{m*n} = X - \boldsymbol{u}\boldsymbol{h} $$

其中，$\boldsymbol{u}$ 是一个 $m$ 维的行向量，$\boldsymbol{u}[m] = \dfrac{1}{n} \sum_{i=1}^{n} X[m, i]$；$h$ 是一个值全为 $1$ 的 $n$ 维行向量。

对于两个随机变量，我们可以利用协方差简单表示这两个变量之间的相关性

$$ \cov \left(x, y\right) = E \left(\left(x - \mu_x\right) \left(x - \mu_x\right)\right) $$

对于已经零均值化后的矩阵 $X'$，计算得出如下矩阵

$$ C = \dfrac{1}{n} X' X'^T = \left\lgroup \begin{array}{cccc} \dfrac{1}{n} \sum_{i=1}^{n} x_{1i}^2 & \dfrac{1}{n} \sum_{i=1}^{n} x_{1i} x_{2i} & \cdots & \dfrac{1}{n} \sum_{}^{} x_{1i} x_{ni} \\ \dfrac{1}{n} \sum_{i=1}^{n} x_{2i} x_{1i} & \dfrac{1}{n} \sum_{i=1}^{n} x_{2i}^2 & \cdots & \dfrac{1}{n} \sum_{}^{} x_{2i} x_{ni} \\ \vdots & \vdots & & \vdots \\ \dfrac{1}{n} \sum_{i=1}^{n} x_{mi} x_{1i} & \dfrac{1}{n} \sum_{i=1}^{n} x_{mi} x_{2i} & \cdots & \dfrac{1}{n} \sum_{}^{} x_{mi}^2 \\ \end{array} \right\rgroup $$

因为矩阵 $X'$ 已经经过了零均值化处理，因此矩阵 $C$ 中对角线上的元素为维度 $m$ 的方差，其他元素则为两个维度之间的协方差。

从 PCA 的目标来看，我们则可以通过求解矩阵 $C$ 的特征值和特征向量，将其特征值按照从大到小的顺序按行重排其对应的特征向量，则取前 $k$ 个，则实现了数据从 $m$ 维降至 $k$ 维。

例如，我们将二维数据

$$ \left\lgroup \begin{array} -1 & -1 & 0 & 0 & 2 \\ -2 & 0 & 0 & 1 & 1 \end{array} \right\rgroup $$

降至一维

x <- matrix(c(-1, -1, 0, 0, 2,
              -2, 0, 0, 1, 1),
            5, 2, byrow = F)
x_pca <- prcomp(x)

print(pca)
# Standard deviations (1, .., p=2):
# [1] 1.5811388 0.7071068
# 
# Rotation (n x k) = (2 x 2):
#            PC1        PC2
# [1,] 0.7071068  0.7071068
# [2,] 0.7071068 -0.7071068

summary(pca)
# Importance of components:
#                           PC1    PC2
# Standard deviation     1.5811 0.7071
# Proportion of Variance 0.8333 0.1667
# Cumulative Proportion  0.8333 1.0000

x_ <- predict(x_pca, x)
print(x_)
#             PC1        PC2
# [1,] -2.1213203  0.7071068
# [2,] -0.7071068 -0.7071068
# [3,]  0.0000000  0.0000000
# [4,]  0.7071068 -0.7071068
# [5,]  2.1213203  0.7071068

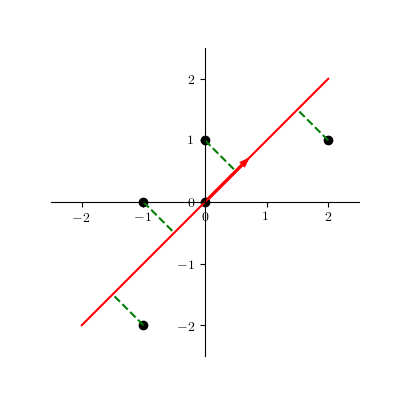
降维的投影结果如图所示

「真诚赞赏，手留余香」

￥ 2 ￥ 5 ￥ 10 ￥ 50 ￥ 100 任意金额