Ising 模型
Ising 模型最早是由物理学家威廉·冷次在 1920 年发明的,他把该模型当成是一个给他学生恩斯特·易辛的问题。易辛在他一篇 1924 年的论文 1 中求得了一维易辛模型的解析解,并且证明它不会产生相变。 二维方晶格易辛模型相对于一维的难出许多,因此其解析的描述在一段时间之后才在 1943 年由拉斯·昂萨格给出 2。
Ising 模型假设铁磁物质是由一堆规则排列的小磁针构成,每个磁针只有上下两个方向。相邻的小磁针之间通过能量约束发生相互作用,同时受到环境热噪声的干扰而发生磁性的随机转变。涨落的大小由关键的温度参数决定,温度越高,随机涨落干扰越强,小磁针越容易发生无序而剧烈地状态转变,从而让上下两个方向的磁性相互抵消,整个系统消失磁性,如果温度很低,则小磁针相对宁静,系统处于能量约束高的状态,大量的小磁针方向一致,铁磁系统展现出磁性。而当系统处于临界温度 $T_C$ 时,Ising 模型表现出一系列幂律行为和自相似现象 3。
由于 Ising 模型的高度抽象,可以很容易地将它应用到其他领域之中。例如,将每个小磁针比喻为某个村落中的村民,而将小磁针上下的两种状态比喻成个体所具备的两种政治观点,相邻小磁针之间的相互作用比喻成村民之间观点的影响,环境的温度比喻成每个村民对自己意见不坚持的程度,这样 Ising 模型就可以建模该村落中不同政治见解的动态演化。在社会科学中,人们已经将 Ising 模型应用于股票市场、种族隔离、政治选择等不同的问题。另一方面,如果将小磁针比喻成神经元细胞,向上向下的状态比喻成神经元的激活与抑制,小磁针的相互作用比喻成神经元之间的信号传导,那么,Ising 模型的变种还可以用来建模神经网络系统,从而搭建可适应环境、不断学习的机器,例如 Hopfield 网络或 Boltzmann 机。
考虑一个二维的情况
如图所示,每个节点都有两种状态 $s_i \in \{+1, -1\}$,则我们可以定义这个系统的能量为
$$ E = -H \sum_{i=1}^{N}{s_i} - J \sum_{<i, j>}{s_i s_j} $$
其中 $H$ 为外界磁场的强度,$J$ 为能量耦合常数,$\sum_{<i, j>}$表示对于相邻的两个节点的函数值求和。因此,可以得出
- 当每个节点的方向同外部磁场一致时,系统能量越小;反之系统能量越大。
- 对于
$J > 0$,当相邻的节点方向相同时,系统能量越小;反之系统能量越大。
对于整个系统的演变,除了系统的总能量以外,还受到节点所处环境的热噪声影响。我们利用温度 $T$ 表示环境对节点的影响,当 $T$ 越高时,节点状态发生变化的可能性越大。此时,则有两种力量作用在每个节点上
- 节点邻居和外部磁场的影响,这种影响使得当前节点尽可能的同其邻居和外部磁场保持一致,即尽可能是系统的总能量达到最小。
- 环境的影响,这种影响使得每个节点的状态以一定的概率发生随机变化。
不难想像,当 $T = 0$ 时,节点状态完全受其邻居和外部磁场影响,当 $J = 0, H = 0$ 时,节点处于完全的随机状态。
对于 Ising 模型,我们利用蒙特卡罗方法进行模拟。初始化系统状态为 $s_i^{\left(0\right)}$,对于任意时刻 $t$,对其状态 $s_i^{\left(t\right)}$进行一个改变,将其中一个节点变为相反的状态,得到新的状态 $s'_i$
$$ s_i^{\left(t+1\right)} = \begin{cases} s'_i & \text{with probablity of } \mu \\ s_i^{\left(t\right)} & \text{with probablity of } 1-\mu \end{cases} $$
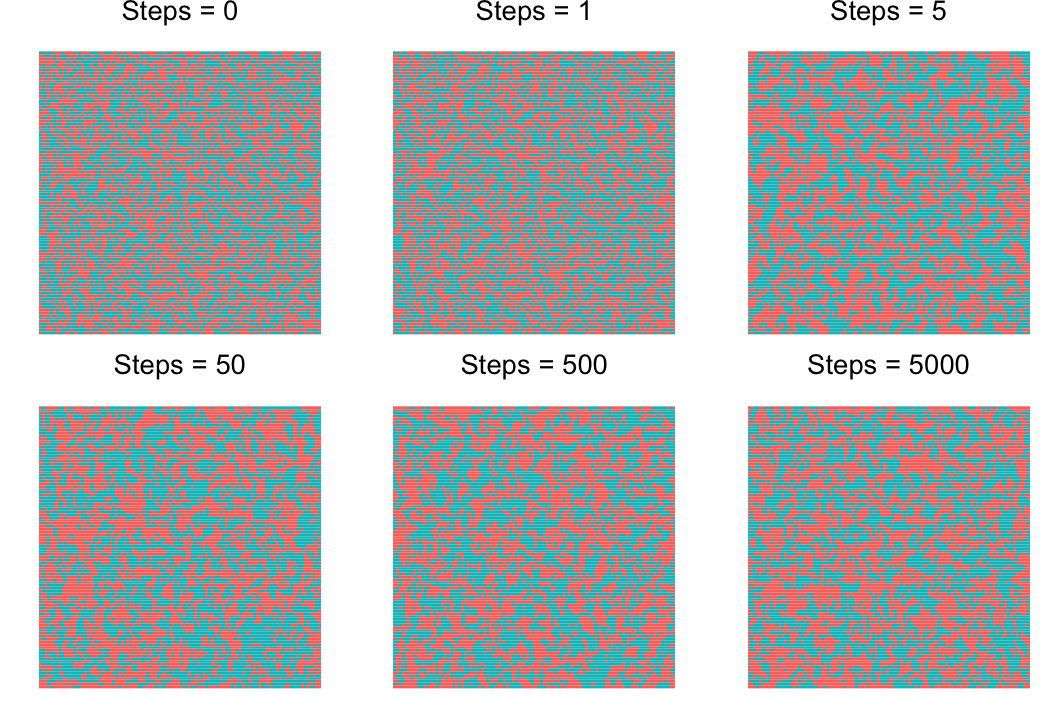
其中 $\mu = \min\left\lbrace\dfrac{e^{E\left(s_i^{\left(t\right)}\right) - E\left(s'_i\right)}}{kT}, 1\right\rbrace$ 表示接受转移的概率;$k \approx 1.38 \times 10^{23}$ 为玻尔兹曼常数。我们利用蒙特卡罗方法对其进行模拟 $T = 4J/k$的情况,我们分别保留第 $0, 1, 5, 50, 500, 5000$ 步的模拟结果
# 每一轮状态转移
each_round <- function(current_matrix, ising_config) {
n_row <- nrow(current_matrix)
n_col <- ncol(current_matrix)
for (i in 1:n_row) {
for (j in 1:n_col) {
current_row <- sample(1:n_row, 1)
current_col <- sample(1:n_col, 1)
s <- current_matrix[current_row, current_col]
e <- -(current_matrix[(current_row-1-1)%%n_row+1, current_col] +
current_matrix[current_row, (current_col-1-1)%%n_col+1] +
current_matrix[(current_row+1)%%n_row, current_col] +
current_matrix[current_row, (current_col+1)%%n_col]) *
s * ising_config$j
mu <- min(exp((e + e) / (ising_config$k * ising_config$t)), 1)
mu_random <- runif(1)
if (mu_random < mu) {
s <- -1 * s
}
current_matrix[current_row, current_col] <- s
}
}
current_matrix
}
# Ising 模拟
ising_simulation <- function(N, iter, ising_config, saved_steps) {
set.seed(112358)
current_matrix <- matrix(sample(0:1, N^2, replace = T), N, N)*2-1
saved_matrix <- list()
if (0 %in% saved_steps) {
saved_matrix <- c(saved_matrix, list(current_matrix))
}
for (i in 1:iter) {
if (i %in% saved_steps) {
saved_matrix <- c(saved_matrix, list(current_matrix))
}
current_matrix <- each_round(current_matrix, ising_config)
if (i %% 1000 == 0) {
cat(paste0("Steps: ", i, '\n'))
}
}
saved_matrix
}
# T = 4J/K,方便模拟取 j = 1, k = 1, t = 4
ising_config <- list(j = 1, k = 1, t = 4)
diff_steps_matrix <- ising_simulation(100, 5000, ising_config,
c(0, 1, 5, 50, 500, 5000))
模拟结果可视化效果如图所示
对于二维的 Ising 模型,存在一个相变点,在相变点上的温度 $T_c$ 满足
$$ \sinh\left(\dfrac{2J_1}{kT_c}\right) \sinh\left(\dfrac{2J_2}{kT_c}\right) = 1 $$
若 $J_1 = J_2$,则
$$ T_c = \dfrac{2J}{k \ln\left(1 + \sqrt{2}\right)} \approx 2.27 \dfrac{J}{k} $$
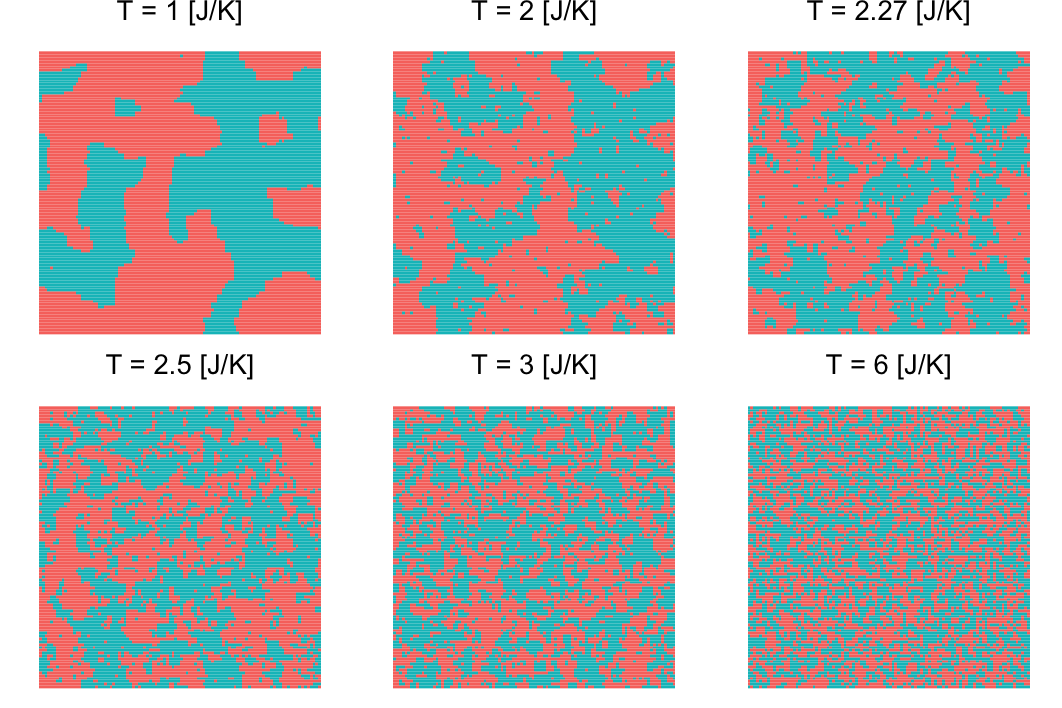
称之为临界温度。当温度小于临界值的时候,Ising 模型中大多数节点状态相同,系统处于较为秩序的状态。当温度大于临界值的时候,大多数节点的状态较为混乱,系统处于随机的状态。而当温度接近临界的时候,系统的运行介于随机与秩序之间,也就是进入了混沌的边缘地带,这种状态称为临界状态。
我们模拟不同温度下,系统在运行 $50$ 步时的状态
ising_config_t <- c(1, 2, 2.27, 2.5, 3, 6)
diff_t_matrix <- lapply(ising_config_t, function(t) {
ising_config <- list(j = 1, k = 1, t = t)
ising_simulation(100, 50, ising_config, c(50))
})
模拟结果可视化效果如图所示
Hopfield 神经网络
Hopfield 神经网络 4 是一种基于能量的反馈人工神经网络。Hopfield 神经网络分为离散型 (Discrete Hopfield Neural Network, DHNN) 和 连续性 (Continues Hopfield Neural Network, CHNN)。
离散型 Hopfield 神经网络
网络结构
对于离散型 Hopfield 神经网络,其网络结果如下
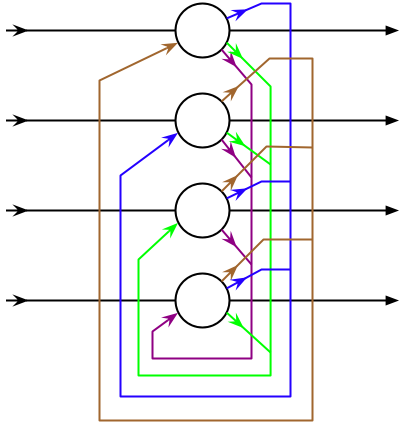
对于具有 $n$ 个神经元的网络,我们设 $t$ 时刻的网络状态为 $\boldsymbol{X}^{\left(t\right)} = \left(x_1^{\left(t\right)}, x_2^{\left(t\right)}, ..., x_n^{\left(t\right)}\right)^T$,对于 $t+1$ 时刻网络的状态
$$ x_i^{\left(t+1\right)} = f \left(net_i\right) $$
其中,DHNN 中 $f$ 多为符号函数,即
$$ \renewcommand{\sign}{\operatorname{sign}} x_i = \sign \left(net_i\right) = \begin{cases} 1, net_i \geq 0 \\ -1, net_i < 0 \end{cases} $$
$net_i$ 为一个节点的输入,为
$$ net_i = \sum_{j=1}^{n}{\left(w_{ij}x_j - T_i\right)} $$
其中 $T_i$ 为每个神经元的阈值,对于 DHNN,一般有 $w_{ii} = 0, w_{ij} = w_{ji}$,当反馈网络稳定后,稳定后的状态即为网络的输出。网络的更新主要有两种状态,异步方式和同步方式。
对于异步方式的更新方法,每一次仅改变一个神经元 $j$ 的状态,即
$$ x_i^{\left(t+1\right)} = \begin{cases} \sign\left(net_i^{\left(t\right)}\right), i = j \\ x_i^{\left(t\right)}, i \neq j \end{cases} $$
对于同步方式的更新方法,每一次需改变所有神经元的状态,即
$$ x_i^{\left(t+1\right)} = \sign\left(net_i^{\left(t\right)}\right) $$
网络稳定性
我们可以将反馈网络看做一个非线性动力学系统,因此这个系统最后可能会收敛到一个稳态,或在有限状态之间振荡,亦或是状态为无穷多个即混沌现象。对于 DHNN 因为其网络状态是有限的,因此不会出现混沌的现象。若一个反馈网络达到一个稳态状态 $\boldsymbol{X}$ 时,即 $\boldsymbol{X}^{\left(t+1\right)} = \boldsymbol{X}^{\left(t\right)}$ ,则称这个状态为一个吸引子。在 Hopfield 网络结构和权重确定的情况下,其具有 $M$ 个吸引子,因此我们可以认为这个网络具有存储 $M$ 个记忆的能力。
设 $\boldsymbol{X}$ 为网络的一个吸引子,权重矩阵 $\boldsymbol{W}$ 是一个对称阵,则定义 $t$ 时刻网络的能量函数为
$$ E\left(t\right) = -\dfrac{1}{2} \boldsymbol{X}^{\left(t\right)T} \boldsymbol{W} \boldsymbol{X}^{\left(t\right)} + \boldsymbol{X}^{\left(t\right)T} \boldsymbol{T} $$
则定义网络能量的变化量
$$ \Delta E\left(t\right) = E\left(t+1\right) - E\left(t\right) $$
则以异步更新方式,不难推导得出
$$ \begin{equation} \begin{split} \Delta E\left(t\right) = -\Delta x_i^{\left(t\right)} \left(\sum_{j=1}^{n}{\left(w_{ij}x_j - T_j\right)}\right) - \dfrac{1}{2} \Delta x_i^{\left(t\right)2} w_{ii} \end{split} \end{equation} $$
由于网络中的神经元不存在自反馈,即 $w_{ii} = 0$,则上式可以化简为
$$ \Delta E\left(t\right) = -\Delta x_i^{\left(t\right)} net_i^{\left(t\right)} $$
因此,对于如上的能量变化,可分为 3 中情况:
- 当
$x_i^{\left(t\right)} = -1, x_i^{\left(t+1\right)} = 1$时,$\Delta x_i^{\left(t\right)} = 2, net_i^{\left(t\right)} \geq 0$,则可得$\Delta E \left(t\right) \leq 0$。 - 当
$x_i^{\left(t\right)} = 1, x_i^{\left(t+1\right)} = -1$时,$\Delta x_i^{\left(t\right)} = -2, net_i^{\left(t\right)} < 0$,则可得$\Delta E \left(t\right) < 0$。 - 当
$x_i^{\left(t\right)} = x_i^{\left(t+1\right)}$时,$\Delta x_i^{\left(t\right)} = 0$,则可得$\Delta E \left(t\right) = 0$。
则对于任何情况,$\Delta E \left(t\right) \leq 0$,也就是说在网络不断变化的过程中,网络的总能量是一直下降或保持不变的,因此网络的能量最终会收敛到一个常数。
设 $\boldsymbol{X}'$ 为吸引子,对于异步更新方式,若存在一个变换顺序,使得网络可以从状态 $\boldsymbol{X}$ 转移到 $\boldsymbol{X}'$,则称 $\boldsymbol{X}$ 弱吸引到 $\boldsymbol{X}'$,这些 $\boldsymbol{X}$ 的集合称之为 $\boldsymbol{X}$ 的弱吸引域;若对于任意变换顺序,都能够使得网络可以从状态 $\boldsymbol{X}$ 转移到 $\boldsymbol{X}'$,则称 $\boldsymbol{X}$ 强吸引到 $\boldsymbol{X}'$,对于这些 $\boldsymbol{X}$ 称之为 $\boldsymbol{X}$ 的强吸引域。
对于 Hopfield 网络的权重,我们利用 Hebbian 规则进行设计。Hebbian 规则认为如果两个神经元同步激发,则它们之间的权重增加;如果单独激发,则权重减少。则对于给定的 $p$ 个模式样本 $\boldsymbol{X}^k, k = 1, 2, ..., p$,其中 $x \in \{-1, 1\}^n$ 且样本之间两两正交,则权重计算公式为
$$ w_{ij} = \dfrac{1}{n} \sum_{k=1}^{p}{x_i^k x_j^k} $$
则对于给定的样本 $\boldsymbol{X}$ 确定为网络的吸引子,但对于有些非给定的样本也可能是网络的吸引子,这些吸引子称之为伪吸引子。以上权重的计算是基于两两正交的样本得到的,但真实情况下很难保证样本两两正交,对于非正交的模式,网络的存储能力则会大大下降。根据 Abu-Mostafa5 的研究表明,当模式的数量 $p$ 大于 $0.15 n$ 时,网络的推断就很可能出错,也就是结果会收敛到伪吸引子上。
示例
我们通过一个手写数字识别的例子介绍一些 Hopfield 网络的功能,我们存在如下 10 个数字的图片,每张为像素 16*16 的二值化图片,其中背景色为白色,前景色为黑色 (每个图片的名称为 num.png,图片位于 /images/cn/2018-01-17-ising-hopfield-and-rbm 目录)。
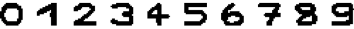
首先我们载入每张图片的数据
library(EBImage)
# 载入数据
digits <- lapply(0:9, function(num) {
readImage(paste0(num, '.png'))
})
# 转换图像为 16*16 的一维向量
# 将 (0, 1) 转换为 (-1, 1)
digits_patterns <- lapply(digits, function(digit) {
pixels <- c(digit)
pixels * 2 - 1
})
接下来利用这 10 个模式训练一个 Hopfield 网络
#' 训练 Hopfield 网络
#'
#' @param n 网络节点个数
#' @param pattern_list 模式列表
#' @return 训练好的 Hopfield 网络
train_hopfield <- function(n, pattern_list) {
weights <- matrix(rep(0, n*n), n, n)
n_patterns <- length(pattern_list)
for (i in 1:n_patterns) {
weights <- weights + pattern_list[[i]] %o% pattern_list[[i]]
}
diag(weights) <- 0
weights <- weights / n_patterns
list(weights = weights, n = n)
}
# 训练 Hopfield 网络
digits_hopfield_network <- train_hopfield(16*16, digits_patterns)
为了测试 Hopfiled 网络的记忆能力,我们利用 10 个模式生成一些测试数据,我们分别去掉图像的右边或下边的 5 个像素,生成新的 20 张测试图片
# 构造测试数据
digits_test_remove_right <- lapply(0:9, function(num) {
digit_test <- digits[[num+1]]
digit_test[12:16, ] <- 1
digit_test
})
digits_test_remove_bottom <- lapply(0:9, function(num) {
digit_test <- digits[[num+1]]
digit_test[, 12:16] <- 1
digit_test
})
digits_test <- c(digits_test_remove_right, digits_test_remove_bottom)
# 转换图像为 16*16 的一维向量
# 将 (0, 1) 转换为 (-1, 1)
digits_test_patterns <- lapply(digits_test, function(digit) {
pixels <- c(digit)
pixels * 2 - 1
})
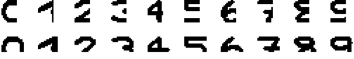
我们利用训练好的 Hopfield 网络运行测试数据,我们迭代 300 次并保存最后的网络输出
#' 运行 Hopfiled 网络
#' @param hopfield_network 训练好的 Hopfield 网络
#' @param pattern 输入的模式
#' @param max_iter 最大迭代次数
#' @param save_history 是否保存状态变化历史
#' @return 最终的模式 (以及历史模式)
run_hopfield <- function(hopfield_network, pattern,
max_iter = 100, save_history = T) {
last_pattern <- pattern
history_patterns <- list()
for (iter in 1:max_iter) {
current_pattern <- last_pattern
i <- round(runif(1, 1, hopfield_network$n))
net_i <- hopfield_network$weights[i, ] %*% current_pattern
current_pattern[i] <- ifelse(net_i < 0, -1, 1)
if (save_history) {
history_patterns[[iter]] <- last_pattern
}
last_pattern <- current_pattern
}
list(history_patterns = history_patterns,
final_pattern = last_pattern)
}
# 运行 Hopfield 网络,获取测试数据结果
digits_test_results_patterns <- lapply(digits_test_patterns,
function(pattern) {
run_hopfield(digits_hopfield_network, pattern, max_iter = 300)
})
# 转换测试数据结果为图片
digits_test_results <- lapply(digits_test_results_patterns,
function(result) {
each_dim <- sqrt(digits_hopfield_network$n)
Image((result$final_pattern + 1) / 2,
dim = c(each_dim, each_dim),
colormode = 'Grayscale')
})
网络变换过程中,图像的变换如图所示
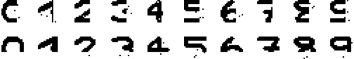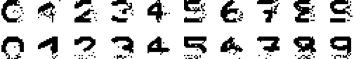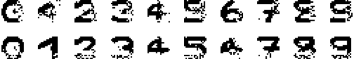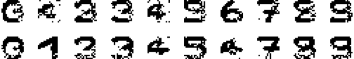
最终网络的输出如图所示
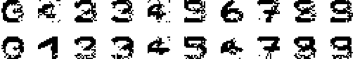
从结果中可以看出,部分测试图片还是得到了比较好的恢复,但如上文所说,由于我们给定的模式之间并不是两两正交的,因此,网络的推断就很可能出错 (例如:数字 5 恢复的结果更像 9 多一些),甚至结果会收敛到伪吸引子上。
连续型 Hopfield 神经网络
网络结构
连续型 Hopfield 网络相比于离散型 Hopfield 网络的主要差别在于:
- 网络中所有的神经元随时间
$t$同时更新,网络状态随时间连续变化。 - 神经元的状态转移函数为一个 S 型函数,例如
$$ v_i = f\left(u_i\right) = \dfrac{1}{1 + e^{\dfrac{-2 u_i}{\gamma}}} = \dfrac{1}{2} \left(1 + \tanh \dfrac{u_i}{\gamma}\right) $$其中,$v_i$表示一个神经元的输出,$u_i$表示一个神经元的输入。
对于理想情况,网络的能量函数可以写为6
$$ E = -\dfrac{1}{2} \sum_{i=1}^{n}{\sum_{j=1}^{n}{w_{ij} v_i v_j}} - \sum_{i=1}^{n} v_i I_i $$
可以得出,随着网络的演变,网络的总能量是降低的,随着网络中节点的不断变化,网络最终收敛到一个稳定的状态。
TSP 问题求解
旅行推销员问题 (Travelling salesman problem, TSP) 是指给定一系列城市和每对城市之间的距离,求解访问每一座城市一次并回到起始城市的最短路径 7。TSP 问题是一个 NP-hard 问题 8。
对于 TSP 问题,我们给定一个城市指之间的距离矩阵
$$ D = \left\lgroup \begin{array}{cccc} d_{11} & d_{12} & \cdots & d_{1n} \\ d_{21} & d_{22} & \cdots & d_{2n} \\ \vdots & \vdots & & \vdots \\ d_{n1} & d_{n2} & \cdots & d_{nn} \end{array} \right\rgroup $$
其中 $d_{ij} = d_{ji}, i \neq j$ 表示城市 $i$ 和城市 $j$ 之间的距离,$d_{ij} = 0, i = j$。TSP 问题的优化目标是找到一条路径访问每一座城市一次并回到起始城市,我们利用一个矩阵表示访问城市的路径
$$ V = \left\lgroup \begin{array}{cccc} v_{11} & v_{12} & \cdots & v_{1n} \\ v_{21} & v_{22} & \cdots & v_{2n} \\ \vdots & \vdots & & \vdots \\ v_{n1} & v_{n2} & \cdots & v_{nn} \end{array} \right\rgroup $$
其中 $v_{xi} = 1$ 表示第 $i$ 次访问城市 $x$,因此对于矩阵 $V$,其每一行每一列仅有一个元素值为 $1$,其他元素值均为 $0$。
对于 TSP 问题,我们可以得到如下约束条件
- 城市约束
因为每个城市只能访问一次,因此对于第 $x$ 行仅能有一个元素是 $1$,其他均为 $0$,即任意两个相邻元素的乘积为 $0$
$$ \sum_{i=1}^{n-1}{\sum_{j=i+1}^{n}{v_{xi}v_{xj}}} = 0 $$
则对于城市约束,我们得到该约束对应的能量分量为
$$ E_1 = \dfrac{1}{2} A \sum_{x=1}^{n}{\sum_{i=1}^{n-1}{\sum_{j=i+1}^{n}{v_{xi}v_{xj}}}} $$
- 时间约束
因为每一时刻仅能够访问一个城市,因此对于第 $i$ 行仅能有一个元素是 $1$,其他均为 $0$,即任意两个相邻元素的乘积为 $0$
$$ \sum_{x=1}^{n-1}{\sum_{y=x+1}^{n}{v_{xi}v_{yi}}} = 0 $$
则对于时间约束,我们得到该约束对应的能量分量为
$$ E_2 = \dfrac{1}{2} B \sum_{i=1}^{n}{\sum_{x=1}^{n-1}{\sum_{y=x+1}^{n}{v_{xi}v_{yi}}}} $$
- 有效性约束
当矩阵 $V$ 中所有的元素均为 $0$ 的时候,可得 $E_1 = 0, E_2 = 0$,但显然这并不是一个有效的路径,因此我们需要保证矩阵 $V$ 中元素值为 $1$ 的个数为 $n$,即
$$ \sum_{x=1}^{n}{\sum_{i=1}^{n}{v_{xi}}} = n $$
则对于有效性约束,我们得到该约束对应的能量分量为
$$ E_3 = \dfrac{1}{2} C \left(\sum_{x=1}^{n}{\sum_{i=1}^{n}{v_{xi}}} - n\right)^2 $$
- 路径长度约束
如上三个约束仅能够保证我们的路径是有效的,但并不一定是最优的。根绝 TSP 问题的优化目标,我们需要引入一个反映路径长度的能量分量,并保证该能量分量随着路径长度的减小而减小。访问两个城市 $x, y$ 有两种形式,$x \to y$ 或 $y \to x$,如果城市 $x$ 和城市 $y$ 在旅行中顺序相邻,则 $v_{xi}v_{y,i+1} = 1, v_{xi}v_{y,i-1} = 0$,反之亦然。则反映路径长度的能量分量可以定义为
$$ E_4 = \dfrac{1}{2} D \sum_{x=1}^{n}{\sum_{y=1}^{n}{\sum_{i=1}^{n}{d_{xy}\left(v_{xi}v_{y,i+1} + v_{xi}v_{y,i-1}\right)}}} $$
综上所述,TSP 问题的能量函数定义为
$$ E = E_1 + E_2 + E_3 + E_4 $$
其中,$A, B, C, D > 0$ 分别为每个能量分量的权重。针对这样的能量函数,我们可得对应神经元 $x_i$ 和 $y_i$ 之间的权重为
$$ \begin{equation} \begin{split} w_{x_i, y_i} = &-2A \delta_{xy} \left(1-\delta_{xy}\right) - 2B \delta_{ij} \left(1-\delta_{xy}\right) \\ &- 2C -2D d_{xy} \left(\delta_{j, i+1} + \delta_{i, j+1}\right) \end{split} \end{equation} $$
其中
$$ \delta_{xy} = \begin{cases} 1, x = y \\ 0, x \neq y \end{cases} , \delta_{ij} = \begin{cases} 1, i = j \\ 0, i \neq j \end{cases} $$
因此可以得到网络关于时间的导数
$$ \begin{equation} \begin{split} \dfrac{d u_{xi}}{d t} = &-2A \sum_{j \neq i}^{n}{v_{xj}} - 2B \sum_{y \neq x}^{n}{v_{yi}} - 2C \left(\sum_{x=1}^{n}{\sum_{j=1}^{n}{v_{xj}}} - n\right) \\ &- 2D \sum_{y \neq x}^{n}{d_{xy}\left(v_{y, i+1} + v_{y, i-1}\right)} - \dfrac{u_{xi}}{\tau} \end{split} \end{equation} $$
据此,我们以一个 10 个城市的数据为例,利用 CHNN 求解 TSP 问题,其中 10 个城市的座标为
| 城市 | 横座标 | 纵座标 |
|---|---|---|
| A | 0.4000 | 0.4439 |
| B | 0.2439 | 0.1463 |
| C | 0.1707 | 0.2293 |
| D | 0.2293 | 0.7610 |
| E | 0.5171 | 0.9414 |
| F | 0.8732 | 0.6536 |
| G | 0.6878 | 0.5219 |
| H | 0.8488 | 0.3609 |
| I | 0.6683 | 0.2536 |
| J | 0.6195 | 0.2634 |
已知的最优路线为 $A \to D \to E \to F \to G \to H \to I \to J \to B \to C \to A$,最优路线的路径长度为 $2.6907$。我们使用如下参数求解 TSP 问题,初始化 $u_{init} = -\dfrac{\gamma}{2} \ln\left(n - 1\right)$,$\gamma = 0.02$,学习率 $\alpha = 0.0001$,神经元激活阈值 $\theta = 0.7$,$\tau = 1$,能量分量权重参数 $A = 500, B = 500, C = 1000, D = 500$,单次迭代最大次数为 1000,共模拟 100 次。
# 城市座标
cities <- data.frame(
l = LETTERS[1:10],
x = c(0.4000, 0.2439, 0.1707, 0.2293, 0.5171,
0.8732, 0.6878, 0.8488, 0.6683, 0.6195),
y = c(0.4439, 0.1463, 0.2293, 0.7610, 0.9414,
0.6536, 0.5219, 0.3609, 0.2536, 0.2634)
)
# 通过城市座标构建距离矩阵
distance_matrix <- function(points) {
n <- nrow(points)
d <- matrix(rep(0, n^2), n, n)
for (i in 1:n) {
for (j in i:n) {
distance <- sqrt((points[i, ]$x - points[j, ]$x)^2 +
(points[i, ]$y - points[j, ]$y)^2)
d[i, j] <- distance
d[j, i] <- distance
}
}
d
}
# 结果约束校验
check_path_valid <- function(v, n) {
# 城市约束
c1 <- 0
for (x in 1:n) {
for (i in 1:(n-1)) {
for (j in (i+1):n) {
c1 <- c1 + v[x, i] * v[x, j]
}
}
}
# 时间约束
c2 <- 0
for (i in 1:n) {
for (x in 1:(n-1)) {
for (y in (x+1):n) {
c2 <- c2 + v[x, i] * v[y, i]
}
}
}
# 有效性约束
c3 <- sum(v)
ifelse(c1 == 0 & c2 == 0 & c3 == n, T, F)
}
# 根据结果矩阵获取路径
v_to_path <- function(v, n) {
p <- c()
for (i in 1:n) {
for (x in 1:n) {
if (v[x, i] == 1) {
p <- c(p, x)
break
}
}
}
p
}
# 计算结果矩阵的路径长度
path_distance <- function(v, n, d) {
p <- v_to_path(v, n)
p <- c(p, p[1])
distance <- 0
for (i in 1:(length(p)-1)) {
distance <- distance + d[p[i], p[i+1]]
}
distance
}
# 构建 Hopfield 网络
tsp_chnn <- function(d, n, gamma = 0.02, alpha = 0.0001,
theta = 0.7, tau = 1,
A = 500, B = 500, C = 1000, D = 500,
max_iter = 1000) {
v <- matrix(runif(n^2), n, n)
u <- matrix(rep(1, n^2), n, n) * (-gamma * log(n-1) / 2)
du <- matrix(rep(0, n^2), n, n)
for (iter in 1:max_iter) {
for (x in 1:n) {
for (i in 1:n) {
# E1
e1 <- 0
for (j in 1:n) {
if (j != i) {
e1 <- e1 + v[x, j]
}
}
e1 <- -A * e1
# E2
e2 <- 0
for (y in 1:n) {
if (y != x) {
e2 <- e2 + v[y, i]
}
}
e2 <- -B * e2
# E3
e3 <- -C * (sum(v) - n)
# E4
e4 <- 0
for (y in 1:n) {
if (y != x) {
e4 <- e4 + d[x, y] *
(v[y, (i+1-1)%%n+1] + v[y, (i-1-1)%%n+1])
}
}
e4 <- -D * e4
du[x, i] <- e1 + e2 + e3 + e4 - u[x, i] / tau
}
}
u <- u + alpha * du
v <- (1 + tanh(u / gamma)) / 2
v <- ifelse(v >= theta, 1, 0)
}
v
}
# 利用 Hopfiled 网络求解 TSP 问题
set.seed(112358)
n <- 10
d <- distance_matrix(cities)
# 模拟 100 次并获取最终结果
tsp_solutions <- lapply(1:100, function(round) {
v <- tsp_chnn(d, n)
valid <- check_path_valid(v, n)
distance <- ifelse(valid, path_distance(v, n, d), NA)
list(round = round, valid = valid,
distance = distance, v = v)
})
# 获取最优结果
best_tsp_solution <- NA
for (tsp_solution in tsp_solutions) {
if (tsp_solution$valid) {
if (!is.na(best_tsp_solution)) {
if (tsp_solution$distance < best_tsp_solution$distance) {
best_tsp_solution <- tsp_solution
}
} else {
best_tsp_solution <- tsp_solution
}
}
}
# 可视化最优结果
best_tsp_solution_path <- v_to_path(best_tsp_solution$v, n)
ordered_cities <- cities[best_tsp_solution_path, ] %>%
mutate(ord = seq(1:10))
best_tsp_solution_path_p <- ggplot(ordered_cities) +
geom_polygon(aes(x, y), color = 'black', fill = NA) +
geom_point(aes(x, y)) +
geom_text(aes(x, y, label = l), vjust = -1) +
geom_text(aes(x, y, label = ord), vjust = 2) +
coord_fixed() + ylim(c(0, 1)) + xlim(c(0, 1)) +
theme(axis.title = element_blank())
print(best_tsp_solution_path_p)
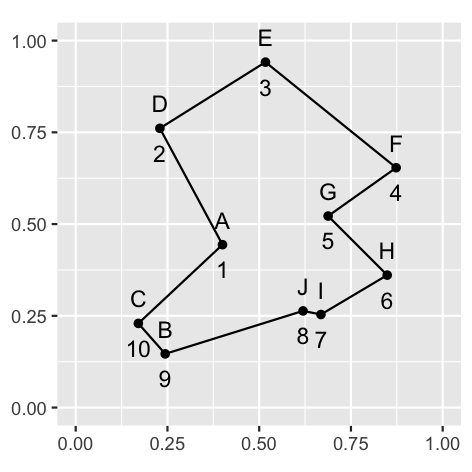
受限的玻尔兹曼机 (RBM)
网络结构及其概率表示
受限的玻尔兹曼机 (Restricted Boltzmann Machine, RBM) 或簧风琴 (harmonium) 是由 Smolensky 与 1986年在玻尔兹曼机 (Boltzmann Machine, BM) 基础上提出的一种随机神经网络 (Stochastic Neural Networks) 9。受限的玻尔兹曼机对于原始的玻尔兹曼机做了相应的限制,在其网络结构中包含可见节点和隐藏节点,并且可见节点和隐藏节点内部不允许存在连接,更加形象的可以将其理解为一个二分图。
对于二值版本的 RBM 而言,其中可见层 $\mathbf{v} = \left(v_1, v_2, ..., v_{n_v}\right)^T$ 由 $n_v$ 个二值随机变量构成;隐藏层 $\mathbf{h} = \left(h_1, h_2, ..., h_{n_h}\right)^T$ 由 $n_h$ 个二值随机变量构成。
RBM 同样作为一个基于能量的模型,其能量函数定义为:
$$ E \left(\boldsymbol{v}, \boldsymbol{h}\right) = -\sum_{i=1}^{n_v}{b_i v_i} -\sum_{j=1}^{n_h}{c_j h_j} - \sum_{i=1}^{n_v}{\sum_{j=1}^{n_h}{v_i w_{i,j} h_i}} $$
将其表示成矩阵向量的形式,可记为:
$$ E \left(\boldsymbol{v}, \boldsymbol{h}\right) = -\boldsymbol{b}^T \boldsymbol{v} - \boldsymbol{c}^T \boldsymbol{h} - \boldsymbol{v}^T \boldsymbol{W} \boldsymbol{h} $$
其中 $\boldsymbol{b} \in \mathbb{R}^{n_v}$ 为可见层的偏置向量;$\boldsymbol{c} \in \mathbb{R}^{n_h}$ 为隐含层的偏置向量;$\boldsymbol{W} \in \mathbb{R}^{n_v \times n_h}$ 为可见层和隐含层之间的权重矩阵。根据能量函数,可得其联合概率分布为:
$$ P \left(\mathbf{v} = \boldsymbol{v}, \mathbf{h} = \boldsymbol{h}\right) = \dfrac{1}{Z} e^{-E \left(\boldsymbol{v}, \boldsymbol{h}\right)} $$
其中 $Z$ 为归一化常数,成为配分函数:
$$ Z = \sum_{\boldsymbol{v}}{\sum_{\boldsymbol{h}}{e^{-E \left(\boldsymbol{v}, \boldsymbol{h}\right)}}} $$
对于 RBM 我们更加关注的的为边缘分布,即:
$$ P \left(\boldsymbol{v}\right) = \sum_{h}{P\left(\boldsymbol{v}, \boldsymbol{h}\right)} = \dfrac{1}{Z} \sum_{h}{e^{-E\left(\boldsymbol{v}, \boldsymbol{h}\right)}} $$
因为概率中包含归一化常数,我们需要计算 $Z$,从其定义可得,当穷举左右可能性的化,我们需要计算 $2^{n_v + n_h}$ 个项,其计算复杂度很大。尽管 $P\left(\boldsymbol{v}\right)$ 计算比较困难,但是其条件概率 $P\left(\mathbf{h} | \mathbf{v}\right)$ 和 $P\left(\mathbf{v} | \mathbf{h}\right)$ 计算和采样相对容易。为了便于推导,我们定义如下记号:
$$ \boldsymbol{h}_{-k} = \left(h_1, h_2, ..., h_{k-1}, h_{k+1}, ..., h_{n_h}\right)^T $$
则 $P\left(h_k = 1 | \boldsymbol{v}\right)$ 定义如下:
$$ \begin{equation} \begin{split} &P\left(h_k = 1 | \boldsymbol{v}\right) \\ = &P\left(h_k = 1 | h_{-k}, \boldsymbol{v}\right) \\ = &\dfrac{P\left(h_k = 1, h_{-k}, \boldsymbol{v}\right)}{P\left(h_{-k}, \boldsymbol{v}\right)} \\ = &\dfrac{P\left(h_k = 1, h_{-k}, \boldsymbol{v}\right)}{P\left(h_k = 1 | h_{-k}, \boldsymbol{v}\right) + P\left(h_k = 0 | h_{-k}, \boldsymbol{v}\right)} \\ = &\dfrac{\dfrac{1}{Z} e^{-E\left(h_k = 1, h_{-k}, \boldsymbol{v}\right)}}{\dfrac{1}{Z} e^{-E\left(h_k = 1, h_{-k}, \boldsymbol{v}\right)} + \dfrac{1}{Z} e^{-E\left(h_k = 0, h_{-k}, \boldsymbol{v}\right)}} \\ = &\dfrac{e^{-E\left(h_k = 1, h_{-k}, \boldsymbol{v}\right)}}{e^{-E\left(h_k = 1, h_{-k}, \boldsymbol{v}\right)} + e^{-E\left(h_k = 0, h_{-k}, \boldsymbol{v}\right)}} \\ = &\dfrac{1}{1 + e^{E\left(h_k = 1, h_{-k}, \boldsymbol{v}\right) - E\left(h_k = 0, h_{-k}, \boldsymbol{v}\right)}} \\ \end{split} \end{equation} $$
其中:
$$ \begin{equation} \begin{split} &E\left(h_k = 1, h_{-k}, \boldsymbol{v}\right) \\ = &E\left(h_k = 1, \boldsymbol{v}\right) \\ = &-\sum_{i=1}^{n_v}{b_i v_i} - \sum_{j=1, j \neq k}^{n_h}{c_j h_j} - \sum_{i=1}^{n_v}{\sum_{j=1, j \neq k}^{n_h}{v_i W_{i, j} h_i}} - c_k - \sum_{i=1}^{n_v}{v_i W_{i, k}} \\ &E\left(h_k = 0, h_{-k}, \boldsymbol{v}\right) \\ = &E\left(h_k = 0, \boldsymbol{v}\right) \\ = &-\sum_{i=1}^{n_v}{b_i v_i} - \sum_{j=1, j \neq k}^{n_h}{c_j h_j} - \sum_{i=1}^{n_v}{\sum_{j=1, j \neq k}^{n_h}{v_i W_{i, j} h_i}} \end{split} \end{equation} $$
因此,$P\left(h_k = 1 | \boldsymbol{v}\right)$ 可以化简为:
$$ \begin{equation} \begin{split} &P\left(h_k = 1 | \boldsymbol{v}\right) \\ = &\dfrac{1}{1 + e^{-\left(c_k + \sum_{i=1}^{n_v}{v_i W_{i, k}}\right)}} \\ = &\sigma\left(c_k + \sum_{i=1}^{n_v}{v_i W_{i, k}}\right) \\ = &\sigma\left(c_k + \boldsymbol{v}^T \boldsymbol{W}_{:, k}\right) \end{split} \end{equation} $$
其中,$\sigma$ 为 sigmoid 函数。因此,我们可以将条件分布表示为连乘的形式:
$$ \begin{equation} \begin{split} P\left(\boldsymbol{h} | \boldsymbol{v}\right) &= \prod_{j=1}^{n_h}{P\left(h_j | \boldsymbol{v}\right)} \\ &= \prod_{j=1}^{n_h}{\sigma\left(\left(2h - 1\right) \odot \left(\boldsymbol{c} + \boldsymbol{W}^T \boldsymbol{v}\right)\right)_j} \end{split} \end{equation} $$
同理可得:
$$ \begin{equation} \begin{split} P\left(\boldsymbol{v} | \boldsymbol{h}\right) &= \prod_{i=1}^{n_v}{P\left(v_i | \boldsymbol{h}\right)} \\ &= \prod_{i=1}^{n_v}{\sigma\left(\left(2v - 1\right) \odot \left(\boldsymbol{b} + \boldsymbol{W} \boldsymbol{h}\right)\right)_i} \end{split} \end{equation} $$
模型训练 10
对于 RBM 模型的训练,假设训练样本集合为 $S = \left\lbrace{\boldsymbol{v^1}, \boldsymbol{v^2}, ..., \boldsymbol{v^{n_s}}}\right\rbrace$,其中 $\boldsymbol{v^i} = \left(v_{1}^{i}, v_{2}^{i}, ..., v_{n_v}^{i}\right), i = 1, 2, ..., n_s$。则训练 RBM 的目标可以定义为最大化如下似然:
$$ \mathcal{L}_{\theta, S} = \prod_{i=1}^{n_s}{P\left(\boldsymbol{v}^i\right)} $$
其中 $\theta$ 为待优化的参数,为了方便计算,等价目标为最大化其对数似然:
$$ \ln\mathcal{L}_{\theta, S} = \ln\prod_{i=1}^{n_s}{P\left(\boldsymbol{v}^i\right)} = \sum_{i=1}^{n_s}{\ln P\left(\boldsymbol{v}^i\right)} $$
我们将其对数似然简写为 $\ln\mathcal{L}_S$ ,通过梯度上升方法,我们可以得到参数的更新公式:
$$ \theta = \theta + \eta \dfrac{\partial \ln\mathcal{L}_S}{\partial \theta} $$
对于单个样本 $\boldsymbol{\color{red}{v'}}$ ,有:
$$ \begin{equation} \begin{split} \dfrac{\partial \ln\mathcal{L}_S}{\partial \theta} &= \dfrac{\partial \ln P\left(\boldsymbol{\color{red}{v'}}\right)}{\partial \theta} = \dfrac{\partial \ln \left(\dfrac{1}{Z} \sum_{\boldsymbol{h}}{e^{-E\left(\boldsymbol{\color{red}{v'}, h}\right)}}\right)}{\partial \theta} \\ &= \dfrac{\partial \left(\ln \sum_{\boldsymbol{h}}{e^{-E\left(\boldsymbol{\color{red}{v'}, h}\right)}} - \ln Z\right)}{\partial \theta} = \dfrac{\partial \left(\ln \sum_{\boldsymbol{h}}{e^{-E\left(\boldsymbol{\color{red}{v'}, h}\right)}} - \ln \sum_{\boldsymbol{v, h}}{e^{-E\left(\boldsymbol{v, h}\right)}}\right)}{\partial \theta} \\ &= \dfrac{\partial}{\partial \theta} \left(\ln \sum_{\boldsymbol{h}}{e^{-E\left(\boldsymbol{\color{red}{v'}, h}\right)}}\right) - \dfrac{\partial}{\partial \theta} \left(\ln \sum_{\boldsymbol{v, h}}{e^{-E\left(\boldsymbol{v, h}\right)}}\right) \\ &= -\dfrac{1}{\sum_{\boldsymbol{h}}{e^{-E\left(\boldsymbol{\color{red}{v'}, h}\right)}}} \sum_{\boldsymbol{h}}{e^{-E\left(\boldsymbol{\color{red}{v'}, h}\right)} \dfrac{\partial E\left(\boldsymbol{\color{red}{v'}, h}\right)}{\partial \theta}} + \dfrac{1}{\sum_{\boldsymbol{v, h}}{e^{-E\left(\boldsymbol{v, h}\right)}}} \sum_{\boldsymbol{v, h}}{e^{-E\left(\boldsymbol{v, h}\right)} \dfrac{\partial E\left(\boldsymbol{v, h}\right)}{\partial \theta}} \\ &= -\sum_{\boldsymbol{h}}{\dfrac{e^{-E\left(\boldsymbol{\color{red}{v'}, h}\right)}}{\sum_{\boldsymbol{h}}{e^{-E\left(\boldsymbol{\color{red}{v'}, h}\right)}}} \dfrac{\partial E\left(\boldsymbol{\color{red}{v'}, h}\right)}{\partial \theta}} + \sum_{\boldsymbol{v, h}}{\dfrac{e^{-E\left(\boldsymbol{v, h}\right)}}{\sum_{\boldsymbol{v, h}}{e^{-E\left(\boldsymbol{v, h}\right)}}} \dfrac{\partial E\left(\boldsymbol{v, h}\right)}{\partial \theta}} \\ &= -\sum_{\boldsymbol{h}}{\dfrac{\dfrac{e^{-E\left(\boldsymbol{\color{red}{v'}, h}\right)}}{Z}}{\dfrac{\sum_{\boldsymbol{h}}{e^{-E\left(\boldsymbol{\color{red}{v'}, h}\right)}}}{Z}} \dfrac{\partial E\left(\boldsymbol{\color{red}{v'}, h}\right)}{\partial \theta}} + \sum_{\boldsymbol{v, h}}{\dfrac{e^{-E\left(\boldsymbol{v, h}\right)}}{\sum_{\boldsymbol{v, h}}{e^{-E\left(\boldsymbol{v, h}\right)}}} \dfrac{\partial E\left(\boldsymbol{v, h}\right)}{\partial \theta}} \\ &= -\sum_{\boldsymbol{h}}{\dfrac{P\left(\boldsymbol{\color{red}{v'}, h}\right)}{P\left(\boldsymbol{\color{red}{v'}}\right)} \dfrac{\partial E\left(\boldsymbol{\color{red}{v'}, h}\right)}{\partial \theta}} + \sum_{\boldsymbol{v, h}}{\dfrac{e^{-E\left(\boldsymbol{v, h}\right)}}{\sum_{\boldsymbol{v, h}}{e^{-E\left(\boldsymbol{v, h}\right)}}} \dfrac{\partial E\left(\boldsymbol{v, h}\right)}{\partial \theta}} \\ &= -\sum_{\boldsymbol{h}}{P\left(\boldsymbol{h | \color{red}{v'}}\right) \dfrac{\partial E\left(\boldsymbol{\color{red}{v'}, h}\right)}{\partial \theta}} + \sum_{\boldsymbol{v, h}}{P\left(\boldsymbol{h | v}\right) \dfrac{\partial E\left(\boldsymbol{v, h}\right)}{\partial \theta}} \end{split} \end{equation} $$
其中:
$$ \begin{equation} \begin{split} \sum_{\boldsymbol{v, h}}{P\left(\boldsymbol{h | v}\right) \dfrac{\partial E\left(\boldsymbol{v, h}\right)}{\partial \theta}} &= \sum_{\boldsymbol{v}}{\sum_{\boldsymbol{h}}{P\left(\boldsymbol{v}\right) P\left(\boldsymbol{h | v}\right) \dfrac{\partial E\left(\boldsymbol{v, h}\right)}{\partial \theta}}} \\ &= \sum_{\boldsymbol{v}}{P\left(\boldsymbol{v}\right) \sum_{\boldsymbol{h}}{P \left(\boldsymbol{h | v}\right) \dfrac{\partial E\left(\boldsymbol{v, h}\right)}{\partial \theta}}} \end{split} \end{equation} $$
则对于参数 $w_{i, j}$ 可得:
$$ \begin{equation} \begin{split} &\sum_{\boldsymbol{h}}{P\left(\boldsymbol{h|v}\right) \dfrac{\partial E\left(\boldsymbol{v, h}\right)}{\partial w_{i, j}}} \\ = &-\sum_{\boldsymbol{h}}{P\left(\boldsymbol{h|v}\right) h_i v_j} \\ = &-\sum_{\boldsymbol{h}}{\prod_{k=1}^{n_h}{P\left(h_k | \boldsymbol{v}\right) h_i v_j}} \\ = &-\sum_{\boldsymbol{h}}{P\left(h_i | \boldsymbol{v}\right) P\left(h_{-i} | \boldsymbol{v}\right) h_i v_j} \\ = &-\sum_{\boldsymbol{h_i}}{\sum_{h_{-i}}{P\left(h_i | \boldsymbol{v}\right) P\left(\boldsymbol{h_{-i}} | \boldsymbol{v}\right) h_i v_j}} \\ = &-\sum_{\boldsymbol{h_i}}{P\left(h_i | \boldsymbol{v}\right) h_i v_j} \sum_{\boldsymbol{h_{-i}}}{P\left(h_{-i} | \boldsymbol{v}\right)} \\ = &-\sum_{\boldsymbol{h_i}}{P\left(h_i | \boldsymbol{v}\right) h_i v_j} \\ = &-\left(P\left(h_i = 0 | \boldsymbol{v}\right) \cdot 0 \cdot v_j + P\left(h_i = 1 | \boldsymbol{v}\right) \cdot 1 \cdot v_j\right) \\ = &-P\left(h_i = 1 | \boldsymbol{v}\right) v_j \end{split} \end{equation} $$
则对于参数 $b_i$ 可得:
$$ \begin{equation} \begin{split} &\sum_{\boldsymbol{h}}{P\left(\boldsymbol{h|v}\right) \dfrac{\partial E\left(\boldsymbol{v, h}\right)}{\partial b_i}} \\ = &-\sum_{\boldsymbol{h}}{P\left(\boldsymbol{h|v}\right) v_i} \\ = &-v_i \sum_{\boldsymbol{h}}{P\left(\boldsymbol{h|v}\right)} \\ = &-v_i \end{split} \end{equation} $$
则对于参数 $c_j$ 可得:
$$ \begin{equation} \begin{split} &\sum_{\boldsymbol{h}}{P\left(\boldsymbol{h|v}\right) \dfrac{\partial E\left(\boldsymbol{v, h}\right)}{\partial c_j}} \\ = &-\sum_{\boldsymbol{h}}{P\left(\boldsymbol{h|v}\right) h_j} \\ = &-\sum_{\boldsymbol{h}}{\prod_{k=1}^{n_h}{P\left(h_k | \boldsymbol{v}\right) h_j}} \\ = &-\sum_{\boldsymbol{h}}{P\left(h_j | \boldsymbol{v}\right) P\left(h_{-j} | \boldsymbol{v}\right) h_j} \\ = &-\sum_{h_j}{\sum_{h_{-j}}{P\left(h_i | \boldsymbol{v}\right) P\left(h_{-j} | \boldsymbol{v}\right) h_j}} \\ = &-\sum_{h_j}{P\left(h_i | \boldsymbol{v}\right) h_j} \sum_{h_{-j}}{P\left(h_{-j} | \boldsymbol{v}\right)} \\ = &-\sum_{h_j}{P\left(h_i | \boldsymbol{v}\right) h_j} \\ = &-\left(P\left(h_j = 0 | \boldsymbol{v}\right) \cdot 0 + P\left(h_j = 1 | \boldsymbol{v}\right) \cdot 1\right) \\ = &-P\left(h_j = 1 | \boldsymbol{v}\right) \end{split} \end{equation} $$
综上所述,可得:
$$ \begin{equation} \begin{split} \dfrac{\partial \ln P\left(\color{red}{\boldsymbol{v'}}\right)}{\partial w_{i, j}} &= -\sum_{\boldsymbol{h}}{P\left(\boldsymbol{h | \color{red}{v'}}\right) \dfrac{\partial E\left(\boldsymbol{\color{red}{v'}, h}\right)}{\partial w_{i, j}}} + \sum_{\boldsymbol{v, h}}{P\left(\boldsymbol{h | v}\right) \dfrac{\partial E\left(\boldsymbol{v, h}\right)}{\partial w_{i, j}}} \\ &= P\left(h_i = 1 | \boldsymbol{\color{red}{v'}}\right) \color{red}{v'_j} - \sum_{\boldsymbol{v}}{P\left(\boldsymbol{v}\right) P\left(h_i = 1 | \boldsymbol{v}\right) v_j}\\ \dfrac{\partial \ln P\left(\color{red}{\boldsymbol{v'}}\right)}{\partial b_i} &= -\sum_{\boldsymbol{h}}{P\left(\boldsymbol{h | \color{red}{v'}}\right) \dfrac{\partial E\left(\boldsymbol{\color{red}{v'}, h}\right)}{\partial b_i}} + \sum_{\boldsymbol{v, h}}{P\left(\boldsymbol{h | v}\right) \dfrac{\partial E\left(\boldsymbol{v, h}\right)}{\partial b_i}} \\ &= \color{red}{v'_i} - \sum_{\boldsymbol{v}}{P\left(\boldsymbol{v}\right) v_i} \\ \dfrac{\partial \ln P\left(\color{red}{\boldsymbol{v'}}\right)}{\partial c_j} &= -\sum_{\boldsymbol{h}}{P\left(\boldsymbol{h | \color{red}{v'}}\right) \dfrac{\partial E\left(\boldsymbol{\color{red}{v'}, h}\right)}{\partial c_j}} + \sum_{\boldsymbol{v, h}}{P\left(\boldsymbol{h | v}\right) \dfrac{\partial E\left(\boldsymbol{v, h}\right)}{\partial c_j}} \\ &= P\left(h_j = 1 | \boldsymbol{\color{red}{v'}}\right) - \sum_{\boldsymbol{v}}{P\left(\boldsymbol{v}\right) P\left(h_j = 1 | \boldsymbol{v}\right)} \\ \end{split} \end{equation} $$
对于多个样本 $S = \left\lbrace{\boldsymbol{v^1}, \boldsymbol{v^2}, ..., \boldsymbol{v^{n_s}}}\right\rbrace$,有:
$$ \begin{equation} \begin{split} \dfrac{\partial \ln \mathcal{L}_S}{\partial w_{i, j}} &= \sum_{m=1}^{n_S}{\left[P\left(h_i = 1 | \boldsymbol{v^m}\right) v_j^m - \sum_{\boldsymbol{v}}{P\left(\boldsymbol{v}\right) P\left(h_i = 1 | \boldsymbol{v} v_j\right)}\right]} \\ \dfrac{\partial \ln \mathcal{L}_S}{\partial b_i} &= \sum_{m=1}^{n_S}{\left[v_i^m - \sum_{\boldsymbol{v}}{P\left(\boldsymbol{v}\right) v_i}\right]} \\ \dfrac{\partial \ln \mathcal{L}_S}{\partial c_j} &= \sum_{m=1}^{n_S}{\left[P\left(h_j = 1 | \boldsymbol{v^m}\right) - \sum_{\boldsymbol{v}}{P\left(\boldsymbol{v}\right) P\left(h_j = 1 | \boldsymbol{v}\right)}\right]} \end{split} \end{equation} $$
针对如上方法,我们需要计算 $\sum_{\boldsymbol{v}}$ 相关项,如上文所述,其计算复杂度为 $O\left(2^{n_v + n_h}\right)$,因为其条件概率计算比较容易,因此我们可以用 Gibbs 采样的方法进行估计,但由于 Gibbs 采样方法存在 burn-in period,因此需要足够次数的状态转移后才能够收敛到目标分布,因此这就增大了利用这种方法训练 RBM 模型的时间。
针对这个问题,Hinton 于 2002 年提出了对比散度 (Contrastive Divergence, CD) 算法 11,基本思想为将训练样本作为采样的初始值,因为目标就是让 RBM 去拟合这些样本的分布,因此这样则可以通过更少的状态转移就收敛到平稳分布。$k$ 步 CD 算法大致步骤为:
- 对
$\forall \boldsymbol{v} \in \boldsymbol{S}$,初始化$\boldsymbol{v}^{\left(0\right)} = \boldsymbol{v}$。 - 执行
$k$步 Gibbs 采样,对于第$t$步,分别利用$P\left(\boldsymbol{h} | \boldsymbol{v}^{\left(t-1\right)}\right)$和$P\left(\boldsymbol{v} | \boldsymbol{h}^{\left(t-1\right)}\right)$采样出$\boldsymbol{h}^{\left(t-1\right)}$和$\boldsymbol{v}^{\left(t\right)}$。 - 利用采样得到的
$\boldsymbol{v}^{\left(k\right)}$近似估计$\sum_{\boldsymbol{v}}$相关项:$$ \begin{equation} \begin{split} \dfrac{\partial \ln P\left(\boldsymbol{v}\right)}{\partial w_{i, j}} &\approx P\left(h_i=1|\boldsymbol{v}^{\left(0\right)}\right) v_j^{\left(0\right)} - P\left(h_i=1|\boldsymbol{v}^{\left(k\right)}\right) v_j^{\left(k\right)} \\ \dfrac{\partial \ln P\left(\boldsymbol{v}\right)}{\partial b_i} &\approx v_i^{\left(0\right)} - v_i^{\left(k\right)} \\ \dfrac{\partial \ln P\left(\boldsymbol{v}\right)}{\partial c_j} &\approx P\left(h_j=1|\boldsymbol{v}^{\left(0\right)}\right) - P\left(h_j=1|\boldsymbol{v}^{\left(k\right)}\right) \end{split} \end{equation} $$
近似估计可以看做是利用
$$ CDK\left(\theta, \boldsymbol{v}\right) = -\sum_{\boldsymbol{h}}{P\left(\boldsymbol{h} | \boldsymbol{v}^{\left(0\right)}\right) \dfrac{\partial E\left(\boldsymbol{v}^{\left(0\right)}, h\right)}{\partial \theta}} + \sum_{\boldsymbol{h}}{P\left(\boldsymbol{h} | \boldsymbol{v}^{\left(k\right)}\right) \dfrac{\partial E\left(\boldsymbol{v}^{\left(k\right)}, \boldsymbol{h}\right)}{\partial \theta}} $$
近似
$$ \dfrac{\partial \ln P\left(\boldsymbol{v}\right)}{\partial \theta} = -\sum_{\boldsymbol{h}}{P\left(\boldsymbol{h} | \boldsymbol{v}^{\left(0\right)}\right) \dfrac{\partial E\left(\boldsymbol{v}^{\left(0\right)}, h\right)}{\partial \theta}} + \sum_{\boldsymbol{v, h}}{P\left(\boldsymbol{v, h}\right) \dfrac{\partial E\left(\boldsymbol{v}, \boldsymbol{h}\right)}{\partial \theta}} $$
的过程。
基于对比散度的 RBM 训练算法可以描述为:
\begin{algorithm}
\caption{CDK 算法}
\begin{algorithmic}
\REQUIRE $k, \boldsymbol{S}, \text{RBM}\left(\boldsymbol{W, b, c}\right)$
\ENSURE $\Delta \boldsymbol{W}, \Delta \boldsymbol{b}, \Delta \boldsymbol{c}$
\PROCEDURE{CDK}{$k, \boldsymbol{S}, \text{RBM}\left(\boldsymbol{W, b, c}\right)$}
\STATE $\Delta \boldsymbol{W} \gets 0, \Delta \boldsymbol{b} \gets 0, \Delta \boldsymbol{c} \gets 0$
\FORALL{$\boldsymbol{v \in S}$}
\STATE $\boldsymbol{v}^{\left(0\right)} \gets \boldsymbol{v}$
\FOR{$t = 0, 1, ..., k-1$}
\STATE $\boldsymbol{h}^{\left(t\right)} \gets \text{sample\_h\_given\_v} \left(\boldsymbol{v}^{\left(t\right)}, \text{RBM}\left(W, b, c\right)\right)$
\STATE $\boldsymbol{v}^{\left(t+1\right)} \gets \text{sample\_v\_given\_h} \left(\boldsymbol{h}^{\left(t\right)}, \text{RBM}\left(W, b, c\right)\right)$
\ENDFOR
\FOR{$i = 1, 2, ..., n_h; j = 1, 2, ..., n_v$}
\STATE $\Delta w_{i, j} \gets \Delta w_{i, j} + \left[P\left(h_i=1|\boldsymbol{v}^{\left(0\right)}\right) v_j^{\left(0\right)} - P\left(h_i=1|\boldsymbol{v}^{\left(k\right)}\right) v_j^{\left(k\right)}\right]$
\STATE $\Delta b_i \gets \Delta b_i = \left[v_i^{\left(0\right)} - v_i^{\left(k\right)}\right]$
\STATE $\Delta c_j \gets \Delta c_j = \left[P\left(h_j=1|\boldsymbol{v}^{\left(0\right)}\right) - P\left(h_j=1|\boldsymbol{v}^{\left(k\right)}\right)\right]$
\ENDFOR
\ENDFOR
\ENDPROCEDURE
\end{algorithmic}
\end{algorithm}
其中,sample_h_given_v 和 sample_v_given_h 分别表示在已知可见层时采样隐含层和在已知隐含层时采样可见层。对于 sample_h_given_v 其算法流程如下:
\begin{algorithm}
\caption{sample\_h\_given\_v 算法}
\begin{algorithmic}
\FOR{$j = 1, 2, ..., n_h$}
\STATE sample $r_j \sim Uniform[0, 1]$
\IF{$r_j < P\left(h_j = 1 | \boldsymbol{v}\right)$}
\STATE $h_j \gets 1$
\ELSE
\STATE $h_j \gets 0$
\ENDIF
\ENDFOR
\end{algorithmic}
\end{algorithm}
类似的,对于 sample_v_given_h 其算法流程如下:
\begin{algorithm}
\caption{sample\_v\_given\_h 算法}
\begin{algorithmic}
\FOR{$j = 1, 2, ..., n_h$}
\STATE sample $r_j \sim Uniform[0, 1]$
\IF{$r_i < P\left(v_i = 1 | \boldsymbol{h}\right)$}
\STATE $v_i \gets 1$
\ELSE
\STATE $v_i \gets 0$
\ENDIF
\ENDFOR
\end{algorithmic}
\end{algorithm}
至此,我们可以得到 RBM 模型训练的整个流程:
\begin{algorithm}
\caption{RBM 训练算法}
\begin{algorithmic}
\FOR{$iter = 1, 2, ..., \text{max\_iter}$}
\STATE $\Delta \boldsymbol{W}, \Delta \boldsymbol{b}, \Delta \boldsymbol{c} \gets \text{CDK} \left(k, \boldsymbol{S}, \text{RBM}\left(\boldsymbol{W, b, c}\right)\right)$
\STATE $\boldsymbol{W} \gets \boldsymbol{W} + \eta \left(\dfrac{1}{n_s} \Delta \boldsymbol{W}\right)$
\STATE $\boldsymbol{b} \gets \boldsymbol{b} + \eta \left(\dfrac{1}{n_s} \Delta \boldsymbol{b}\right)$
\STATE $\boldsymbol{c} \gets \boldsymbol{c} + \eta \left(\dfrac{1}{n_s} \Delta \boldsymbol{c}\right)$
\ENDFOR
\end{algorithmic}
\end{algorithm}
其中,$k$ 为 CDK 算法参数,$\text{max\_iter}$ 为最大迭代次数,$\boldsymbol{S}$ 为训练样本,$n_s = |\boldsymbol{S}|$,$\eta$ 为学习率。
对于模型的评估,最简单的是利用 RBM 模型的似然或对数似然,但由于涉及到归一化因子 $Z$ 的计算,其复杂度太高。更常用的方式是利用重构误差 (reconstruction error),即输入数据和利用 RBM 模型计算得到隐含节点再重构回可见节点之间的误差。
MNIST 示例
我们利用经典的 MNIST 数据作为示例,我们利用基于 tensorflow 的扩展包 tfrbm 12。tfrbm 实现了 Bernoulli-Bernoulli RBM 和 Gaussian-Bernoulli RBM 两种不同的 RBM,两者的比较详见 13 14。
import numpy as np
from matplotlib import pyplot as plt, gridspec
from tfrbm import BBRBM, GBRBM
from tensorflow.examples.tutorials.mnist import input_data
# 读入训练数据和测试数据
mnist = input_data.read_data_sets('MNIST', one_hot=True)
mnist_train_images = mnist.train.images
mnist_test_images = mnist.test.images
mnist_test_labels = mnist.test.labels
MNIST 数据集中,训练集共包含 55000 个样本,每个样本的维度为 784,我们构建 Bernoulli-Bernoulli RBM,设置隐含节点个数为 64,学习率为 0.01,epoches 为 30,batch size 为 10。
bbrbm = BBRBM(n_visible=784,
n_hidden=64,
learning_rate=0.01,
use_tqdm=True)
bbrbm_errs = bbrbm.fit(mnist_train_images, n_epoches=30, batch_size=10)
# Epoch: 0: 100%|##########| 5500/5500 [00:11<00:00, 480.39it/s]
# Train error: 0.1267
#
# ......
#
# Epoch: 29: 100%|##########| 5500/5500 [00:11<00:00, 482.15it/s]
# Train error: 0.0347
训练误差变化如下
plt.style.use('ggplot')
plt.plot(bbrbm_errs)
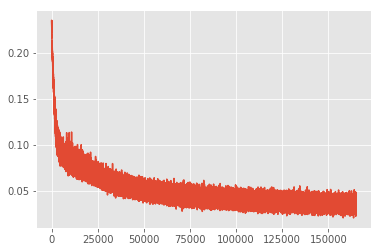
我们从 MNIST 的测试集中针对每个数字选取 10 个样本,共 100 个样本作为测试数据,利用训练好的 RBM 模型重构这 100 个样本
mnist_test_images_samples = np.zeros([10 * 10, 784])
mnist_test_images_samples_rec = np.zeros([10 * 10, 784])
mnist_test_images_samples_plt = np.zeros([10 * 10 * 2, 784])
digits_current_counts = np.zeros(10, dtype=np.int32)
digits_total_counts = np.ones(10, dtype=np.int32) * 10
for idx in range(mnist_test_images.shape[0]):
image = mnist_test_images[idx, ]
label = mnist_test_labels[idx, ]
for digit in range(10):
digit_label = np.zeros(10)
digit_label[digit] = 1
if (label == digit_label).all() and
digits_current_counts[digit] < 10:
nrow = digits_current_counts[digit]
sample_idx = nrow * 10 + digit
mnist_test_images_samples[sample_idx, ] = image
mnist_test_images_samples_rec[sample_idx, ] = \
bbrbm.reconstruct(image.reshape([1, -1]))
mnist_test_images_samples_plt[sample_idx * 2, ] = \
mnist_test_images_samples[sample_idx, ]
mnist_test_images_samples_plt[sample_idx * 2 + 1, ] = \
mnist_test_images_samples_rec[sample_idx, ]
digits_current_counts[digit] += 1
if (digits_current_counts == digits_total_counts).all():
break
对比测试输入数据和重构结果,奇数列为输入数据,偶数列为重构数据
def plot_mnist(mnist_images, nrows, ncols, cmap='gray'):
fig = plt.figure(figsize=(ncols, nrows))
gs = gridspec.GridSpec(nrows, ncols)
gs.update(wspace=0.025, hspace=0.025)
for nrow in range(nrows):
for ncol in range(ncols):
ax = plt.subplot(gs[nrow, ncol])
idx = nrow * ncols + ncol
minist_image = mnist_images[idx, ].reshape([28, 28])
ax.imshow(minist_image, cmap=cmap)
ax.axis('off')
return fig
plot_mnist(mnist_test_images_samples_plt, 10, 20)
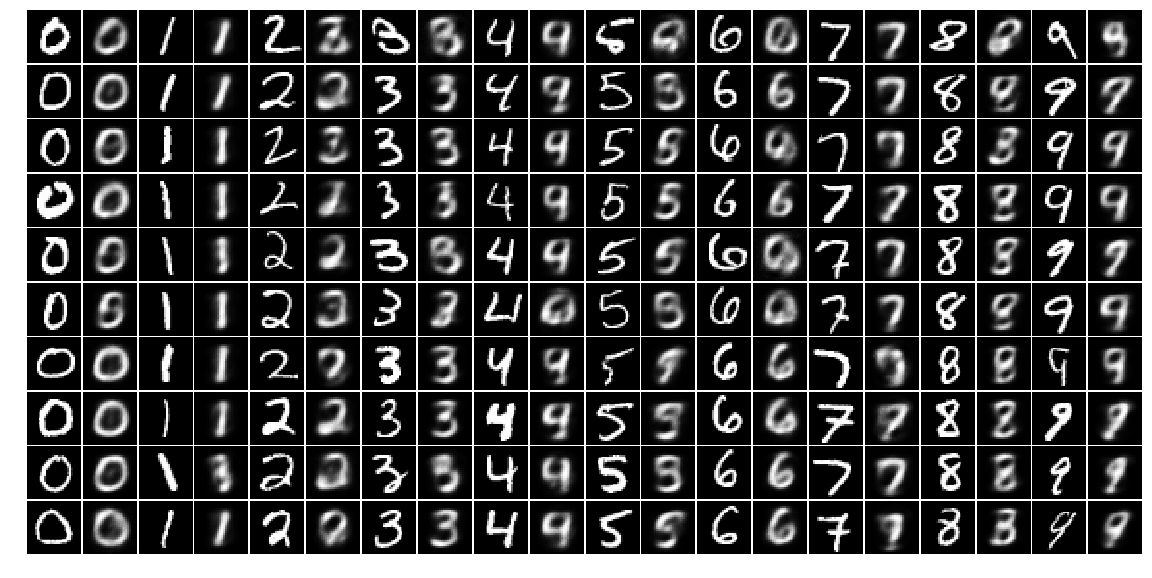
测试集上的重构误差为
gbrbm.get_err(mnist_test_images_samples)
# 0.035245348
-
Ernest Ising, Beitrag zur Theorie des Ferround Paramagnetismus (1924) Contribution to the Theory of Ferromagnetism (English translation of “Beitrag zur Theorie des Ferromagnetismus”, 1925) Goethe as a Physicist (1950) ↩︎
-
Onsager, L. “A two-dimensional model with an order–disorder transition (crystal statistics I).” Phys. Rev 65 (1944): 117-49. ↩︎
-
Hopfield, John J. “Neural networks and physical systems with emergent collective computational abilities.” Spin Glass Theory and Beyond: An Introduction to the Replica Method and Its Applications. 1987. 411-415. ↩︎
-
Abu-Mostafa, Y. A. S. E. R., and J. St Jacques. “Information capacity of the Hopfield model.” IEEE Transactions on Information Theory 31.4 (1985): 461-464. ↩︎
-
韩力群. 人工神经网络理论、设计及应用 ↩︎
-
Smolensky, Paul. Information processing in dynamical systems: Foundations of harmony theory. No. CU-CS-321-86. COLORADO UNIV AT BOULDER DEPT OF COMPUTER SCIENCE, 1986. ↩︎
-
Hinton, Geoffrey E. “Training products of experts by minimizing contrastive divergence.” Neural computation 14.8 (2002): 1771-1800. ↩︎
-
Hinton, Geoffrey. “A practical guide to training restricted Boltzmann machines.” Momentum 9.1 (2010): 926. ↩︎
-
Yamashita, Takayoshi, et al. “To be Bernoulli or to be Gaussian, for a Restricted Boltzmann Machine.” Pattern Recognition (ICPR), 2014 22nd International Conference on. IEEE, 2014. ↩︎

