序列到序列 (Seq2Seq) 和注意力机制 (Attention Machanism)
范叶亮 / 2018-10-12
分类: 深度学习, 表示学习, 自然语言处理 / 标签: 序列, seq2seq, Sequence to Sequence, Encoder, Decoder, Beam Search, 注意力机制, Attention Mechanism, 自注意力, Self-attention, Intra-attention / 字数: 8159
Encoder-Decoder & Seq2Seq
Encoder-Decoder 是一种包含两个神经网络的模型,两个网络分别扮演编码器和解码器的角色。Cho 等人 1 提出了一个基于 RNN 的 Encoder-Decoder 神经网络用于机器翻译。网络结构如下图所示:
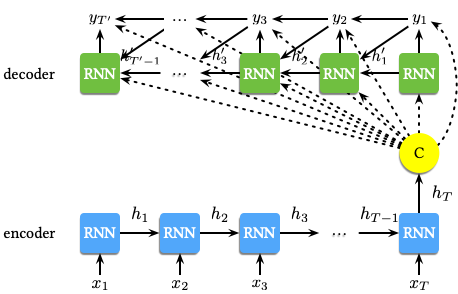
整个模型包含编码器 (Encoder) 和解码器 (Decoder) 两部分:Encoder 将一个可变长度的序列转换成为一个固定长度的向量表示,Decoder 再将这个固定长度的向量表示转换为一个可变长度的序列。这使得模型可以处理从一个可变长度序列到另一个可变长度序例的转换,即学习到对应的条件概率 $p \left(y_1, \dotsc, y_{T'} | x_1, \dotsc, x_T\right)$,其中 $T$ 和 $T'$ 可以为不同的值,也就是说输入和输出的序列的长度不一定相同。
在模型中,Encoder 为一个 RNN,逐次读入输入序列 $\mathbf{x}$ 中的每个元素,其中 RNN 隐状态的更新方式如下:
$$ \mathbf{h}_{\langle t \rangle} = f \left(\mathbf{h}_{\langle t-1 \rangle}, x_t\right) $$
在读入序列的最后一个元素后 (通常为一个结束标记),RNN 的隐状态则为整个输入序列的概括信息 $\mathbf{c}$。Decoder 为另一个 RNN,用于根据隐状态 $\mathbf{h}'_{\langle t \rangle}$ 预测下一个元素 $y_t$,从而生成整个输出序列。不同于 Encoder 中的 RNN,Decoder 中 RNN 的隐状态 $\mathbf{h}'_{\langle t \rangle}$ 除了依赖上一个隐含层的状态和之前的输出外,还依赖整个输入序列的概括信息 $\mathbf{c}$,即:
$$ \mathbf{h}'_{\langle t \rangle} = f \left(\mathbf{h}'_{\langle t-1 \rangle}, y_{t-1}, \mathbf{c}\right) $$
类似的,下一个输出元素的条件分布为:
$$ P \left(y_t | y_{t-1}, y_{t-2}, \dotsc, y_1, \mathbf{c}\right) = g \left(\mathbf{h}_{\langle t \rangle}, y_{t-1}, \mathbf{c}\right) $$
RNN Encoder-Decoder 的两部分通过最大化如下的对数似然函数的联合训练进行优化:
$$ \max_{\theta} \dfrac{1}{N} \sum_{n=1}^{N}{\log p_{\theta} \left(\mathbf{y}_n | \mathbf{x}_n\right)} $$
其中,$\theta$ 为模型的参数,$\mathbf{x}_n$ 和 $\mathbf{y}_n$ 分别为输入和输出序列的成对样本。当模型训练完毕后,我们可以利用模型根据给定的输入序列生成相应的输出序列,或是根据给定的输入和输出序列对计算概率得分 $p_{\theta} \left(\mathbf{y} | \mathbf{x}\right)$。同时,作者还提出了一种新的 RNN 单元 GRU (Gated Recurrent Unit),有关 GRU 的更多介绍请参见 之前的博客。
序列到序列 (Sequence to Sequence, Seq2Seq) 模型从名称中不难看出来是一种用于处理序列数据到序列数据转换问题 (例如:机器翻译等) 的方法。Sutskever 等人 2 提出了一种基于 Encoder-Decoder 网络结构的 Seq2Seq 模型用于机器翻译,网络结构细节同 RNN Encoder-Decoder 略有不同,如下图所示:
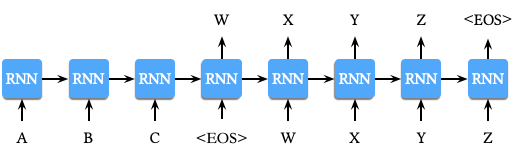
模型的相关细节如下:
- 对数据进行预处理,在每个句子的结尾添加特殊字符
<EOS>,如上图所示。首先计算A, B, C, <EOS>的表示,再利用该表示计算W, X, Y, Z, <EOS>的条件概率。 - 利用两个不同的 LSTM,一个用于输入序列,另一个用于输出序列。
- 选用一个较深的 LSTM 模型 (4 层) 提升模型效果。
- 对输入序列进行倒置处理,例如对于输入序列
$a, b, c$和对应的输出序列$\alpha, \beta, \gamma$,LSTM 需要学习的映射关系为$c, b, a \to \alpha, \beta, \gamma$。
在模型的解码阶段,模型采用简单的从左到右的 Beam Search,该方法维护一个大小为 $B$ 的集合保存最好的结果。下图展示了 $B = 2$ 情况下 Beam Search 的具体工作方式:
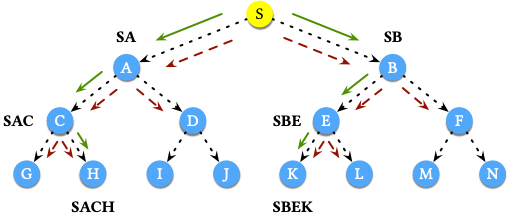
其中,红色的虚线箭头表示每一步可能的搜索方向,绿色的实线箭头表示每一步概率为 Top $B$ 的方向。例如,从 S 开始搜索:
- 第一步搜索的可能结果为 SA 和 SB,保留 Top 2,结果为 SA 和 SB。
- 第二步搜索的可能结果为 SAC,SAD,SBE 和 SBF,保留 Top 2,结果为 SAC 和 SBE。
- 第三步搜索的可能结果为 SACG,SACH,SBEK 和 SBEL,保留 Top 2,结果为 SACH 和 SBEK。至此,整个搜索结束。
Bahdanau 等人 3 提出了一种基于双向 RNN (Bidirectional RNN, BiRNN) 结合注意力机制 (Attention Mechanism) 的网络结构用于机器翻译。网络结构如下:
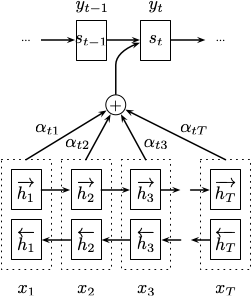
模型的编码器使用了一个双向的 RNN,前向的 RNN $\overrightarrow{f}$ 以从 $x_1$ 到 $x_T$ 的顺序读取输入序列并计算前向隐状态 $\left(\overrightarrow{h}_1, \dotsc, \overrightarrow{h}_T\right)$,后向的 RNN $\overleftarrow{f}$ 以从 $x_T$ 到 $x_1$ 的顺序读取输入序列并计算后向隐状态 $\left(\overleftarrow{h}_1, \dotsc, \overleftarrow{h}_T\right)$。对于一个词 $x_j$,通过将对应的前向隐状态 $\overrightarrow{h}_j$ 和后向隐状态 $\overleftarrow{h}_j$ 进行拼接得到最终的隐状态 $h_j = \left[\overrightarrow{h}_j^{\top}; \overleftarrow{h}_j^{\top}\right]^{\top}$。这样的操作使得隐状态 $h_j$ 既包含了前面词的信息也包含了后面词的信息。
在模型的解码器中,对于一个给定的序例 $\mathbf{x}$,每一个输出的条件概率为:
$$ p \left(y_i | y_1, \dotsc, y_{i-1}, \mathbf{x}\right) = g \left(y_{i-1}, s_i, c_i\right) $$
其中,$s_i$ 为 $i$ 时刻 RNN 隐含层的状态,即:
$$ s_i = f \left(s_{i-1}, y_{i-1}, c_i\right) $$
这里需要注意的是不同于之前的 Encoder-Decoder 模型,此处每一个输出词 $y_i$ 的条件概率均依赖于一个单独的上下文向量 $c_i$。该部分的改进即结合了注意力机制,有关注意力机制的详细内容将在下个小节中展开说明。
注意力机制 (Attention Mechanism)
Bahdanau 等人在文中 3 提出传统的 Encoder-Decoder 模型将输入序列压缩成一个固定长度的向量 $c$,但当输入的序例很长时,尤其是当比训练集中的语料还长时,模型的的效果会显著下降。针对这个问题,如上文所述,上下文向量 $c_i$ 依赖于 $\left(h_1, \dotsc, h_T\right)$。其中,每个 $h_i$ 都包含了整个序列的信息,同时又会更多地关注第 $i$ 个词附近的信息。对于 $c_i$,计算方式如下:
$$ c_i = \sum_{j=1}^{T}{\alpha_{ij} h_j} $$
对于每个 $h_j$ 的权重 $\alpha_{ij}$,计算方式如下:
$$ \alpha_{ij} = \dfrac{\exp \left(e_{ij}\right)}{\sum_{k=1}^{T}{\exp \left(e_{ik}\right)}} $$
其中,$e_{ij} = a \left(s_{i-1}, h_j\right)$ 为一个 Alignment 模型,用于评价对于输入的位置 $j$ 附近的信息与输出的位置 $i$ 附近的信息的匹配程度。Alignment 模型 $a$ 为一个用于评分的前馈神经网络,与整个模型进行联合训练,计算方式如下:
$$ a \left(s_{i-1}, h_j\right) = v_a^{\top} \tanh \left(W_a s_{i-1} + U_a h_j\right) $$
其中,$W_a \in \mathbb{R}^{n \times n}, U_a \in \mathbb{R}^{n \times 2n},v_a \in \mathbb{R}^n$ 为网络的参数。
Hard & Soft Attention
Xu 等人 4 在图像标题生成 (Image Caption Generation) 任务中引入了注意力机制。在文中作者提出了 Hard Attenttion 和 Soft Attention 两种不同的注意力机制。
对于 Hard Attention 而言,令 $s_t$ 表示在生成第 $t$ 个词时所关注的位置变量,$s_{t, i} = 1$ 表示当第 $i$ 个位置用于提取视觉特征。将注意力位置视为一个中间潜变量,可以以一个参数为 $\left\{\alpha_i\right\}$ 的多项式分布表示,同时将上下文向量 $\hat{\mathbf{z}}_t$ 视为一个随机变量:
$$ \begin{equation} \begin{split} & p \left(s_{t, i} = 1 | s_{j < t}, \mathbf{a}\right) = \alpha_{t, i} \\ & \hat{\mathbf{z}}_t = \sum_{i}{s_{t, i} \mathbf{a}_i} \end{split} \end{equation} $$
因此 Hard Attention 可以依据概率值从隐状态中进行采样计算得到上下文向量,同时为了实现梯度的反向传播,需要利用蒙特卡罗采样的方法来估计梯度。
对于 Soft Attention 而言,则直接计算上下文向量 $\hat{\mathbf{z}}_t$ 的期望,计算方式如下:
$$ \mathbb{E}_{p \left(s_t | a\right)} \left[\hat{\mathbf{z}}_t\right] = \sum_{i=1}^{L}{\alpha_{t, i} \mathbf{a}_i} $$
其余部分的计算方式同 Bahdanau 等人 3 的论文类似。Soft Attention 模型可以利用标准的反向传播算法进行求解,直接嵌入到整个模型中一同训练,相对更加简单。
下图展示了一些图片标题生成结果的可视化示例,其中图片内 白色 为关注的区域,画线的文本 即为生成的标题中对应的词。

Global & Local Attention
Luong 等人 5 提出了 Global Attention 和 Local Attention 两种不同的注意力机制用于机器翻译。Global Attention 的思想是在计算上下文向量 $c_t$ 时将编码器的所有隐状态均考虑在内。对于对齐向量 $\boldsymbol{a}_t$,通过比较当前目标的隐状态 $\boldsymbol{h}_t$ 与每一个输入的隐状态 $\bar{\boldsymbol{h}}_s$ 得到,即:
$$ \begin{equation} \begin{split} \boldsymbol{a}_t &= \text{align} \left(\boldsymbol{h}_t, \bar{\boldsymbol{h}}_s\right) \\ &= \dfrac{\exp \left(\text{score} \left(\boldsymbol{h}_t, \bar{\boldsymbol{h}}_s\right)\right)}{\sum_{s'}{\exp \left(\text{score} \left(\boldsymbol{h}_t, \bar{\boldsymbol{h}}_{s'}\right)\right)}} \end{split} \end{equation} $$
其中 $\text{score}$ 为一个基于内容 (content-based) 的函数,可选的考虑如下三种形式:
$$ \text{score} \left(\boldsymbol{h}_t, \bar{\boldsymbol{h}}_s\right) = \begin{cases} \boldsymbol{h}_t^{\top} \bar{\boldsymbol{h}}_s & dot \\ \boldsymbol{h}_t^{\top} \boldsymbol{W}_a \bar{\boldsymbol{h}}_s & general \\ \boldsymbol{W}_a \left[\boldsymbol{h}_t; \bar{\boldsymbol{h}}_s\right] & concat \end{cases} $$
我们利用一个基于位置 (location-based) 的函数构建注意力模型,其中对齐分数通过目标的隐状态计算得到:
$$ \boldsymbol{a}_t = \text{softmax} \left(\boldsymbol{W}_a \boldsymbol{h}_t\right) $$
Global Attention 模型的网络结构如下所示:
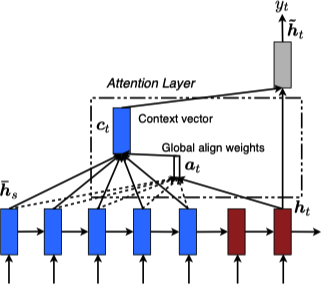
Global Attention 的一个问题在于任意一个输出都需要考虑输入端的所有隐状态,这对于很长的文本 (例如:一个段落或一篇文章) 计算量太大。Local Attention 为了解决这个问题,首先在 $t$ 时刻对于每个目标词生成一个对齐位置 $p_t$,其次上下文向量 $\boldsymbol{c}_t$ 则由以 $p_t$ 为中心前后各 $D$ 大小的窗口 $\left[p_t - D, p_t + D\right]$ 内的输入的隐状态计算得到。不同于 Global Attention,Local Attention 的对齐向量 $\boldsymbol{a}_t \in \mathbb{R}^{2D + 1}$ 为固定维度。
一个比较简单的做法是令 $p_t = t$,也就是假设输入和输出序列是差不多是单调对齐的,我们称这种做法为 Monotonic Alignment (local-m)。另一种做法是预测 $p_t$,即:
$$ p_t = S \cdot \text{sigmoid} \left(\boldsymbol{v}_p^{\top} \tanh \left(\boldsymbol{W}_p \boldsymbol{h}_t\right)\right) $$
其中,$\boldsymbol{W}_p$ 和 $\boldsymbol{h}_t$ 为预测位置模型的参数,$S$ 为输入句子的长度。我们称这种做法为 Predictive Alignment (local-p)。作为 $\text{sigmoid}$ 函数的结果,$p_t \in \left[0, S\right]$,则通过一个以 $p_t$ 为中心的高斯分布定义对齐权重:
$$ \boldsymbol{a}_t \left(s\right) = \text{align} \left(\boldsymbol{h}_t, \bar{\boldsymbol{h}}_s\right) \exp \left(- \dfrac{\left(s - p_t\right)^2}{2 \sigma^2}\right) $$
其中,根据经验设置 $\sigma = \dfrac{D}{2}$,$s$ 为在窗口大小内的一个整数。
Local Attention 模型的网络结构如下所示:
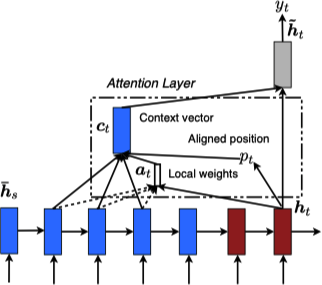
Self Attention
Vaswani 等人 6 提出了一种新的网络结构,称之为 Transformer,其中采用了自注意力 (Self-attention) 机制。自注意力是一种将同一个序列的不同位置进行自我关联从而计算一个句子表示的机制。Transformer 利用堆叠的 Self Attention 和全链接网络构建编码器 (下图左) 和解码器 (下图右),整个网络架构如下图所示:
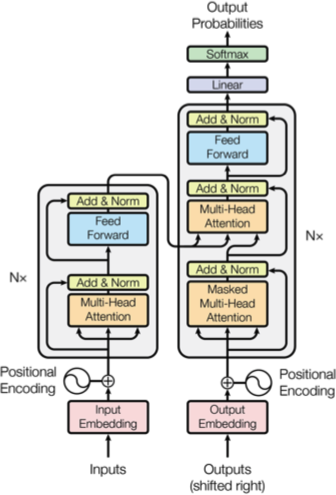
编码器和解码器
编码器 是由 $N = 6$ 个相同的网络层构成,每层中包含两个子层。第一层为一个 Multi-Head Self-Attention 层,第二层为一个 Position-Wise 全链接的前馈神经网络。每一层再应用一个残差连接 (Residual Connection) 7 和一个层标准化 (Layer Normalization) 8。则每一层的输出为 $\text{LayerNorm} \left(x + \text{Sublayer} \left(x\right)\right)$,其中 $\text{Sublayer} \left(x\right)$ 为子层本身的函数实现。为了实现残差连接,模型中所有的子层包括 Embedding 层的输出维度均为 $d_{\text{model}} = 512$。
解码器 也是由 $N = 6$ 个相同的网络层构成,但每层中包含三个子层,增加的第三层用于处理编码器的输出。同编码器一样,每一层应用一个残差连接和一个层标准化。除此之外,解码器对 Self-Attention 层进行了修改,确保对于位置 $i$ 的预测仅依赖于位置在 $i$ 之前的输出。
Scaled Dot-Product & Multi-Head Attention
一个 Attention 函数可以理解为从一个序列 (Query) 和一个键值对集合 (Key-Value Pairs Set) 到一个输出的映射。文中提出了一种名为 Scaled Dot-Product Attention (如下图所示),其中输入包括 queries,维度为 $d_k$ 的 keys 和维度为 $d_v$ 的 values。通过计算 queries 和所有 keys 的点积,除以 $\sqrt{d_k}$,再应用一个 softmax 函数获取 values 的权重。
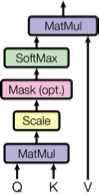
实际中,我们会同时计算一个 Queries 集合中的 Attention,并将其整合成一个矩阵 $Q$。Keys 和 Values 也相应的整合成矩阵 $K$ 和 $V$,则有:
$$ \text{Attention} \left(Q, K, V\right) = \text{softmax} \left(\dfrac{Q K^{\top}}{\sqrt{d_k}}\right) V $$
其中,$Q \in \mathbb{R}^{n \times d_k}$,$Q$ 中的每一行为一个 query,$K \in \mathbb{R}^{n \times d_k}, V \in \mathbb{R}^{n \times d_v}$。$\dfrac{1}{\sqrt{d_k}}$ 为一个归一化因子,避免点积的值过大导致 softmax 之后的梯度过小。
Multi-Head Attention 的做法并不直接对原始的 keys,values 和 queries 应用注意力函数,而是学习一个三者各自的映射再应用 Atteneion,同时将这个过程重复 $h$ 次。Multi-Head Attention 的网路结构如下图所示:
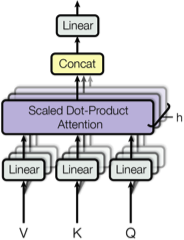
Multi-Head Attention 的计算过程如下所示:
$$ \begin{equation} \begin{split} \text{MultiHead} \left(Q, K, V\right) &= \text{Concat} \left(\text{head}_1, \dotsc, \text{head}_h\right) W^O \\ \textbf{where } \text{head}_i &= \text{Attention} \left(QW_i^Q, KW_i^K, VW_i^V\right) \end{split} \end{equation} $$
其中,$W_i^Q \in \mathbb{R}^{d_{\text{model}} \times d_k}, W_i^K \in \mathbb{R}^{d_{\text{model}} \times d_k}, W_i^V \in \mathbb{R}^{d_{\text{model}} \times d_v}, W_i^O \in \mathbb{R}^{h d_v \times d_{\text{model}}}, $ 为映射的参数,$h = 8$ 为重复的次数,则有 $d_k = d_v = d_{\text{model}} / h = 64$。
整个 Transformer 模型在三处使用了 Multi-Head Attention,分别是:
- Encoder-Decoder Attention Layers,其中 queries 来自于之前的 Decoder 层,keys 和 values 来自于 Encoder 的输出,该部分同其他 Seq2Seq 模型的 Attention 机制类似。
- Encoder Self-Attention Layers,其中 queries,keys 和 values 均来自之前的 Encoder 层的输出,同时 Encoder 层中的每个位置都能够从之前层的所有位置获取到信息。
- Decoder Self-Attention Layers,其中 queries,keys 和 values 均来自之前的 Decoder 层的输出,但 Decoder 层中的每个位置仅可以从之前网络层的包含当前位置之前的位置获取信息。
Position-wise Feed-Forward Networks
在 Encoder 和 Decoder 中的每一层均包含一个全链接的前馈神经网络,其使用两层线性变换和一个 ReLU 激活函数实现:
$$ \text{FFN} \left(x\right) = \max \left(0, x W_1 + b_1\right) W_2 + b_2 $$
全链接层的输入和输出的维度 $d_{\text{model}} = 512$,内层的维度 $d_{ff} = 2048$。
Positional Encoding
Transformer 模型由于未使用任何循环和卷积组件,因此为了利用序列的位置信息则在模型的 Embedding 输入中添加了 Position Encoding。Position Encoding 的维度同 Embedding 的维度相同,从而可以与 Embedding 进行加和,文中使用了如下两种形式:
$$ \begin{equation} \begin{split} PE_{\left(pos, 2i\right)} &= \sin \left(pos / 10000^{2i / d_{\text{model}}}\right) \\ PE_{\left(pos, 2i+1\right)} &= \cos \left(pos / 10000^{2i / d_{\text{model}}}\right) \end{split} \end{equation} $$
其中,$pos$ 为位置,$i$ 为对应的维度,选用这种表示形式的原因是对于一个固定的偏移 $k$,$PE_{pos + k}$ 都可以利用 $PE_{pos}$ 线性表示。这是因为对于正弦和余弦函数有:
$$ \begin{equation} \begin{split} \sin \left(\alpha + \beta\right) &= \sin \alpha \cos \beta + \cos \alpha \sin \beta \\ \cos \left(\alpha + \beta\right) &= \cos \alpha \sin \beta - \sin \alpha \sin \beta \end{split} \end{equation} $$
Why Self-Attention
相比于循环和卷积层,Transformer 模型利用 Self-Attention 层用于一个序列 $\left(x_1, \dotsc, x_n\right)$ 到另一个等长序例 $\left(z_1, \dotsc, z_n\right)$ 的映射,其中 $x_i, z_i \in \mathbb{R}^d$。Self-Attention 与循环和卷积的对比如下表所示:
| 层类型 | 每层的复杂度 | 序列操作数 | 长距离依赖路径长度 |
|---|---|---|---|
| Self-Attention | $O \left(n^2 \cdot d\right)$ |
$O \left(1\right)$ |
$O \left(1\right)$ |
| Recurrent | $O \left(n \cdot d^2\right)$ |
$O \left(n\right)$ |
$O \left(n\right)$ |
| Convolutional | $O \left(k \cdot n \cdot d^2\right)$ |
$O \left(1\right)$ |
$O \left(\log_k \left(n\right)\right)$ |
| Self-Attention (restricted) | $O \left(r \cdot n \cdot d\right)$ |
$O \left(1\right)$ |
$O \left(n/r\right)$ |
- 对于每层的复杂度,当序例的长度
$n$比表示的维度$d$小时,Self-Attention 要比循环结构计算复杂度小。为了改进在长序列上 Self-Attention 的计算性能,Self-Attention 可以被限制成仅考虑与输出位置对应的输入序列位置附近$r$窗口大小内的信息。 - Recurrent 层的最小序列操作数为
$O \left(n\right)$,其他情况为$O \left(1\right)$,这使得 Recurrent 的并行能力较差,即上表中的 Self-Attention (restricted)。 - 学习到长距离依赖是很多序列任务的关键,影响该能力的一个重要因素就是前向和后向信号穿越整个网络的路径长度,这个路径长度越短,越容易学习到长距离依赖。
Attention Visualizations
第一张图展示了 Self-Attention 学到的句子内部的一个长距离依赖 “making … more diffcult”,图中不同的颜色表示不同 Head 的 Attention,颜色越深表示 Attention 的值越大。
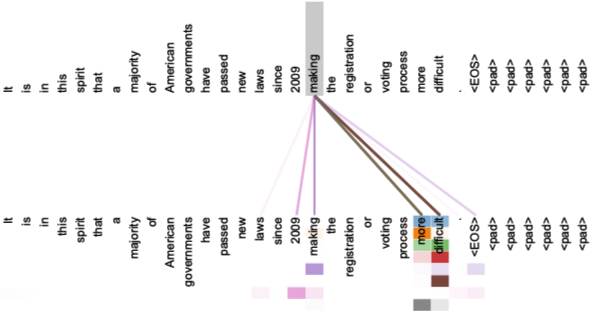
第二张图展示了 Self-Attention 学到的一个指代消解关系 (Anaphora Resolution),its 指代的为上文中的 law。下图 (上) 为 Head 5 的所有 Attention,下图 (下) 为 Head 5 和 6 关于词 its 的 Attention,不难看出模型学习到了 its 和 law 之间的依赖关系 (指代消解关系)。
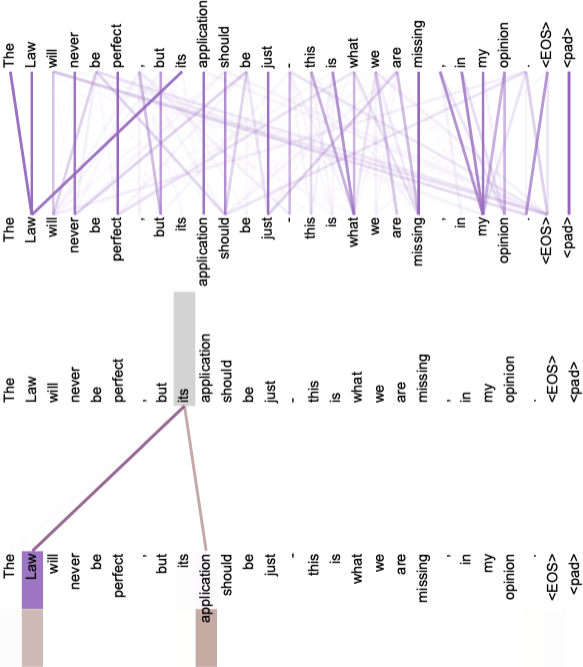
Hierarchical Attention
Yang 等人 9 提出了一种层级的注意力 (Hierarchical Attention) 网络用于文档分类。Hierarchical Attention 共包含 4 层:一个词编码器 (Word Encoder),一个词级别的注意力层 (Word Attention),一个句子编码器 (Sentence Encoder) 和一个句子级别的注意力层 (Sentence Attention)。网络架构如下图所示:
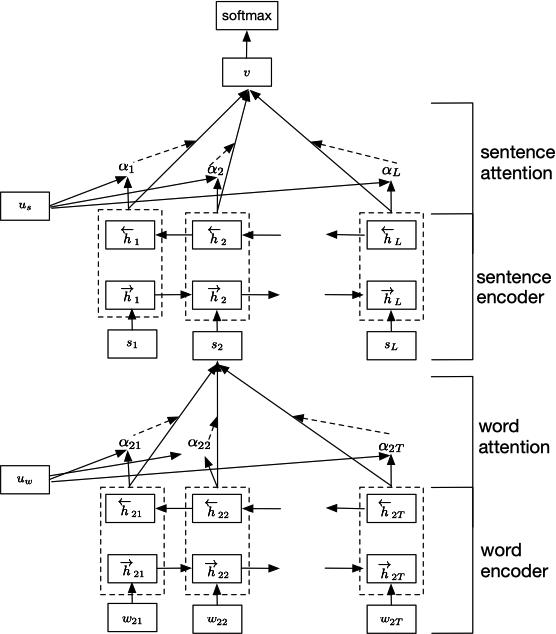
Word Encoder
对于一个给定的句子 $w_{it}, t \in \left[0, T\right]$,通过一个 Embedding 矩阵 $W_e$ 得到每个词的向量表示,再应用一个双向的 GRU,即:
$$ \begin{equation} \begin{split} x_{it} &= W_e w_{it}, t \in \left[1, T\right] \\ \overrightarrow{h}_{it} &= \overrightarrow{\text{GRU}} \left(x_{it}\right), t \in \left[1, T\right] \\ \overleftarrow{h}_{it} &= \overleftarrow{\text{GRU}} \left(x_{it}\right), t \in \left[T, 1\right] \end{split} \end{equation} $$
最后将前向的隐状态 $\overrightarrow{h}_{it}$ 和后向的隐状态 $\overleftarrow{h}_{it}$ 进行拼接,得到 $h_{ij} = \left[\overrightarrow{h}_{it}, \overleftarrow{h}_{it}\right]$ 为整个句子在词 $w_{ij}$ 附近的汇总信息。
Word Attention
Word Attention 同一般的 Attention 机制类似,计算方式如下:
$$ \begin{equation} \begin{split} u_{it} &= \tanh \left(W_w h_{it} + b_w\right) \\ a_{it} &= \dfrac{\exp \left(u_{it}^{\top} u_w\right)}{\sum_{t}{\exp \left(u_{it}^{\top} u_w\right)}} \\ s_i &= \sum_{t}{a_{it} h_{it}} \end{split} \end{equation} $$
Sentence Encoder
在 Word Attention 之后,我们得到了一个句子的表示 $s_i$,类似的我们利用一个双向的 GRU 编码文档中的 $L$ 个句子:
$$ \begin{equation} \begin{split} \overrightarrow{h}_i &= \overrightarrow{\text{GRU}} \left(s_i\right), i \in \left[1, L\right] \\ \overleftarrow{h}_i &= \overleftarrow{\text{GRU}} \left(s_i\right), i \in \left[L, 1\right] \end{split} \end{equation} $$
最后将前向的隐状态 $\overrightarrow{h}_i$ 和后向的隐状态 $\overleftarrow{h}_i$ 进行拼接,得到 $h_i = \left[\overrightarrow{h}_i, \overleftarrow{h}_i\right]$ 为整个文档关于句子 $s_i$ 的注意力汇总信息。
Sentence Attention
同理可得 Sentence Attention 的计算方式如下:
$$ \begin{equation} \begin{split} u_i &= \tanh \left(W_s h_i + b_s\right) \\ a_i &= \dfrac{\exp \left(u_i^{\top} u_s\right)}{\sum_{i}{\exp \left(u_i^{\top} u_s\right)}} \\ v &= \sum_{i}{a_i h_i} \end{split} \end{equation} $$
最终得到整个文档的向量表示 $v$。
Attention-over-Attention
Cui 等人 10 提出了 Attention-over-Attention 的模型用于阅读理解 (Reading Comprehension)。网络结构如下图所示:
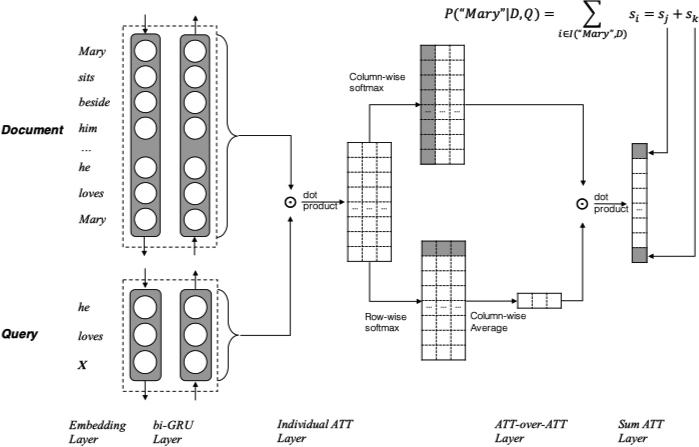
对于一个给定的训练集 $\langle \mathcal{D}, \mathcal{Q}, \mathcal{A} \rangle$,模型包含两个输入,一个文档 (Document) 和一个问题序列 (Query)。网络的工作流程如下:
- 先获取 Document 和 Query 的 Embedding 结果,再应用一个双向的 GRU 得到对应的隐状态
$h_{doc}$和$h_{query}$。 - 计算一个 Document 和 Query 的匹配程度矩阵
$M \in \mathbb{R}^{\lvert \mathcal{D} \rvert \times \lvert \mathcal{Q} \rvert}$,其中第$i$行第$j$列的值计算方式如下:$$ M \left(i, j\right) = h_{doc} \left(i\right)^{\top} \cdot h_{query} \left(j\right) $$ - 按照 列 的方向对矩阵
$M$应用 softmax 函数,矩阵中的每一列为考虑一个 Query 中的词的 Document 级别的 Attention,因此定义$\alpha \left(t\right) \in \mathbb{R}^{\lvert \mathcal{D} \rvert}$为$t$时刻的 Document 级别 Attention (query-to-document attention)。计算方式如下:$$ \begin{equation} \begin{split} \alpha \left(t\right) &= \text{softmax} \left(M \left(1, t\right), \dotsc, M \left(\lvert \mathcal{D} \rvert, t\right)\right) \\ \alpha &= \left[\alpha \left(1\right), \alpha \left(2\right), \dotsc, \alpha \left(\lvert \mathcal{Q} \rvert\right)\right] \end{split} \end{equation} $$ - 同理按照 行 的方向对矩阵
$M$应用 softmax 函数,可以得到$\beta \left(t\right) \in \mathbb{R}^{\lvert \mathcal{Q} \rvert}$为$t$时刻的 Query 级别的 Attention (document-to-query attention)。计算方式如下:$$ \beta \left(t\right) = \text{softmax} \left(M \left(t, 1\right), \dotsc, M \left(t, \lvert \mathcal{Q} \rvert\right)\right) $$ - 对于 document-to-query attention,我们对结果进行平均得到:
$$ \beta = \dfrac{1}{n} \sum_{t=1}^{\lvert \mathcal{D} \rvert}{\beta \left(t\right)} $$ - 最终利用
$\alpha$和$\beta$的点积$s = \alpha^{\top} \beta \in \mathbb{R}^{\lvert \mathcal{D} \rvert}$得到 attended document-level attention (即 attention-over-attention)。
Multi-step Attention
Gehring 等人 11 提出了基于 CNN 和 Multi-step Attention 的模型用于机器翻译。网络结构如下图所示:
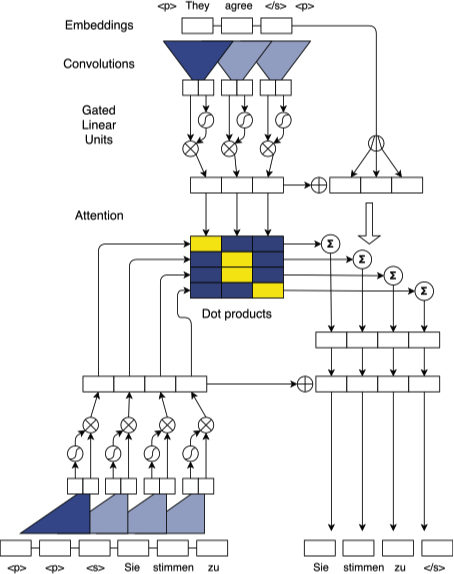
Position Embeddings
模型首先得到序列 $\mathbf{x} = \left(x_1, \dotsc, x_m\right)$ 的 Embedding $\mathbf{w} = \left(w_1, \dotsc , w_m\right), w_j \in \mathbb{R}^f$。除此之外还将输入序列的位置信息映射为 $\mathbf{p} = \left(p_1, \dotsc, p_m\right), p_j \in \mathbb{R}^f$,最终将两者进行合并得到最终的输入 $\mathbf{e} = \left(w_1 + p_1, \dotsc, w_m + p_m\right)$。同时在解码器部分也采用类似的操作,将其与解码器网络的输出表示合并之后再喂入解码器网络 $\mathbf{g} = \left(g_1, \dotsc, g_n\right)$ 中。
Convolutional Block Structure
编码器和解码器均由多个 Convolutional Block 构成,每个 Block 包含一个卷积计算和一个非线性计算。令 $\mathbf{h}^l = \left(h_1^l, \dotsc, h_n^l\right)$ 表示解码器第 $l$ 个 Block 的输出,$\mathbf{z}^l = \left(z_1^l, \dotsc, z_m^l\right)$ 表示编码器第 $l$ 个 Block 的输出。对于一个大小 $k = 5$ 的卷积核,其结果的隐状态包含了这 5 个输入,则对于一个 6 层的堆叠结构,结果的隐状态则包含了输入中的 25 个元素。
在每一个 Convolutional Block 中,卷积核的参数为 $W \in \mathbb{R}^{2d \times kd}, b_w \in \mathbb{R}^{2d}$,其中 $k$ 为卷积核的大小,经过卷积后的输出为 $Y \in \mathbb{R}^{2d}$。之后的非线性层采用了 Dauphin 等人 12 提出的 Gated Linear Units (GLU),对于卷积后的输出 $Y = \left[A, B\right]$ 有:
$$ v \left(\left[A, B\right]\right) = A \otimes \sigma \left(B\right) $$
其中,$A, B \in \mathbb{R}^d$ 为非线性单元的输入,$\otimes$ 为逐元素相乘,$\sigma \left(B\right)$ 为用于控制输入 $A$ 与当前上下文相关度的门结构。
模型中还加入了残差连接,即:
$$ h_i^l = v \left(W^l \left[h_{i-k/2}^{l-1}, \dotsc, h_{i+k/2}^{l-1}\right] + b_w^l\right) + h_i^{l-1} $$
为了确保网络卷积层的输出同输入的长度相匹配,模型对输入数据的前后填补 $k - 1$ 个零值,同时为了避免解码器使用当前预测位置之后的信息,模型删除了卷积输出尾部的 $k$ 个元素。在将 Embedding 喂给编码器网络之前,在解码器输出应用 softmax 之前以及所有解码器层计算 Attention 分数之前,建立了一个从 Embedding 维度 $f$ 到卷积输出大小 $2d$ 的线性映射。最终,预测下一个词的概率计算方式如下:
$$ p \left(y_{i+1} | y_1, \dotsc, y_i, \mathbf{x}\right) = \text{softmax} \left(W_o h_i^L + b_o\right) \in \mathbb{R}^T $$
Multi-step Attention
模型的解码器网络中引入了一个分离的注意力机制,在计算 Attention 时,将解码器当前的隐状态 $h_i^l$ 同之前输出元素的 Embedding 进行合并:
$$ d_i^l = W_d^l h_i^l + b_d^l + g_i $$
对于解码器网络层 $l$ 中状态 $i$ 和输入元素 $j$ 之间的的 Attention $a_{ij}^l$ 通过解码器汇总状态 $d_i^l$ 和最后一个解码器 Block $u$ 的输出 $z_j^u$ 进行点积运算得到:
$$ a_{ij}^l = \dfrac{\exp \left(d_i^l \cdot z_j^u\right)}{\sum_{t=1}^{m}{\exp \left(d_i^l \cdot z_t^u\right)}} $$
条件输入 $c_i^l$ 的计算方式如下:
$$ c_i^l = \sum_{j=1}^{m}{a_{ij}^l \left(z_j^u + e_j\right)} $$
其中,$e_j$ 为输入元素的 Embedding。与传统的 Attention 不同,$e_j$ 的加入提供了一个有助于预测的具体输入元素信息。
最终将 $c_i^l$ 加到对应的解码器层的输出 $h_i^l$。这个过程与传统的单步 Attention 不同,被称之为 Multiple Hops 13。这种方式使得模型在计算 Attention 时会考虑之前已经注意过的输入信息。
-
Cho, K., van Merrienboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., & Bengio, Y. (2014). Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP) (pp. 1724–1734). ↩︎
-
Sutskever, I., Vinyals, O., & Le, Q. V. (2014). Sequence to Sequence Learning with Neural Networks. In Z. Ghahramani, M. Welling, C. Cortes, N. D. Lawrence, & K. Q. Weinberger (Eds.), Advances in Neural Information Processing Systems 27 (pp. 3104–3112). ↩︎
-
Bahdanau, D., Cho, K., & Bengio, Y. (2014). Neural Machine Translation by Jointly Learning to Align and Translate. arXiv preprint arXiv:1409.0473 ↩︎ ↩︎ ↩︎
-
Xu, K., Ba, J., Kiros, R., Cho, K., Courville, A., Salakhudinov, R., … Bengio, Y. (2015). Show, Attend and Tell: Neural Image Caption Generation with Visual Attention. In International Conference on Machine Learning (pp. 2048–2057). ↩︎
-
Luong, T., Pham, H., & Manning, C. D. (2015). Effective Approaches to Attention-based Neural Machine Translation. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing (pp. 1412–1421). ↩︎
-
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., … Polosukhin, I. (2017). Attention is All you Need. In I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, & R. Garnett (Eds.), Advances in Neural Information Processing Systems 30 (pp. 5998–6008). ↩︎
-
He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep Residual Learning for Image Recognition. In 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (pp. 770–778). ↩︎
-
Ba, J. L., Kiros, J. R., & Hinton, G. E. (2016). Layer Normalization. arXiv preprint arXiv:1607.06450 ↩︎
-
Yang, Z., Yang, D., Dyer, C., He, X., Smola, A., & Hovy, E. (2016). Hierarchical Attention Networks for Document Classification. In Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (pp. 1480–1489). ↩︎
-
Cui, Y., Chen, Z., Wei, S., Wang, S., Liu, T., & Hu, G. (2017). Attention-over-Attention Neural Networks for Reading Comprehension. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers) (pp. 593–602). ↩︎
-
Gehring, J., Auli, M., Grangier, D., Yarats, D., & Dauphin, Y. N. (2017). Convolutional Sequence to Sequence Learning. In International Conference on Machine Learning (pp. 1243–1252). ↩︎
-
Dauphin, Y. N., Fan, A., Auli, M., & Grangier, D. (2016). Language Modeling with Gated Convolutional Networks. arXiv preprint arXiv:1612.08083 ↩︎
-
Sukhbaatar, S., szlam, arthur, Weston, J., & Fergus, R. (2015). End-To-End Memory Networks. In C. Cortes, N. D. Lawrence, D. D. Lee, M. Sugiyama, & R. Garnett (Eds.), Advances in Neural Information Processing Systems 28 (pp. 2440–2448). ↩︎