计算复杂性 (Computational Complexity) 与动态规划 (Dynamic Programming)
范叶亮 / 2018-11-18
分类: 最优化 / 标签: 计算复杂性, Computational Complexity, 函数的增长, P 问题, NP 问题, NP Complete 问题, NP Hard 问题, 动态规划, Dynamic Programming, 背包问题, Knapsack Problem, 最长公共子序列, Longest Common Subsequence, 最长公共子串, Longest Common Substring, 最短路问题, Shortest Path Problem, Floyd-Warshall 算法 / 字数: 5272
计算复杂性
计算复杂性 (Computational Complexity) 是用于对一个问题求解所需的资源 (通常为 空间 和 时间) 的度量。在评估一个算法的时候,除了算法本身的准确性以外,同时需要关注算法运行的时间以及占用的内存,从而根据实际情况选择合适的算法。
函数的增长
计算复杂性中的空间和时间的评估方法类似,在此我们更多的以时间复杂度为例。算法的运行时间刻画了算法的效率,对于一个输入规模为 $n$ 的问题,定义一个算法求解该问题 最坏情况 下的运行时间为 $T \left(n\right)$,我们可以使用一些 渐进记号 更加方便地对其进行描述。
$\Theta$记号
对于一个给定的函数 $g \left(n\right)$,$\Theta \left(g \left(n\right)\right)$ 可以表示如下函数的集合:
$$ \Theta \left(g \left(n\right)\right) = \left\{f \left(n\right): \exists c_1 > 0, c_2 > 0, n_0 > 0, s.t. \forall n \geq n_0, 0 \leq c_1 g \left(n\right) \leq f \left(n\right) \leq c_2 g \left(n\right) \right\} $$
也就是说当 $n$ 足够大时,函数 $f \left(n\right)$ 能够被 $c_1 g \left(n\right)$ 和 $c_2 g \left(n\right)$ 夹在中间,我们称 $g \left(n\right)$ 为 $f \left(n\right)$ 的一个 渐进紧确界 (Asymptotically Tight Bound)。
$O$记号
$\Theta$ 记号给出了一个函数的上界和下界,当只有一个 渐进上界 时,可使用 $O$ 记号。$O \left(g \left(n\right)\right)$ 表示的函数集合为:
$$ O \left(g \left(n\right)\right) = \left\{f \left(n\right): \exists c > 0, n_0 > 0, s.t. \forall n \geq n_0, 0 \leq f \left(n\right) \leq c g \left(n\right)\right\} $$
$O$ 记号描述的为函数的上界,因此可以用它来限制算法在最坏情况下的运行时间。
$\Omega$记号
$\Omega$ 记号提供了 渐进下界,其表示的函数集合为:
$$ \Omega \left(g \left(n\right)\right) = \left\{f \left(n\right): \exists c > 0, n_0 > 0, s.t. \forall n \geq n_0, 0 \leq c g \left(n\right) \leq f \left(n\right)\right\} $$
根据上面的三个渐进记号,不难证明如下定理:
$o$记号
$O$ 记号提供的渐进上界可能是也可能不是渐进紧确的,例如 $2n^2 = O \left(n^2\right)$ 是渐进紧确的,但 $2n = O \left(n^2\right)$ 是非渐进紧确的。我们使用 $o$ 记号表示非渐进紧确的上界,其表示的函数集合为:
$$ o \left(g \left(n\right)\right) = \left\{f \left(n\right): \forall c > 0, \exists n_0 > 0, s.t. \forall n \geq n_0, 0 \leq f \left(n\right) < c g \left(n\right)\right\} $$
$\omega$记号
$\omega$ 记号与 $\Omega$ 记号的关系类似于 $o$ 记号与 $O$ 记号的关系,我们使用 $\omega$ 记号表示一个非渐进紧确的下界,其表示的函数集合为:
$$ \omega \left(g \left(n\right)\right) = \left\{f \left(n\right): \forall c > 0, \exists n_0 > 0, s.t. \forall n \geq n_0, 0 \leq c g \left(n\right) < f \left(n\right)\right\} $$
NP 完全性
计算问题可以按照在不同计算模型下所需资源的不同予以分类,从而得到一个对算法问题“难度”的类别,这就是复杂性理论中复杂性类概念的来源 1。对于输入规模为 $n$ 的问题,一个算法在最坏情况下的运行时间为 $O \left(n^k\right)$,其中 $k$ 为一个确定的常数,我们称这类算法为 多项式时间的算法。
本节我们将介绍四类问题:P 类问题,NP 类问题,NPC 类问题和 NPH 类问题。
- P 类问题
P 类问题 (Polynomial Problem,多项式问题) 是指能在多项式时间内 解决 的问题。
- NP 类问题
NP 类问题 (Non-Deteministic Polynomial Problem,非确定性多项式问题) 是指能在多项式时间内被 证明 的问题,也就是可以在多项式时间内对于一个给定的解验证其是否正确。所有的 P 类问题都是 NP 类问题,但目前 (截至 2018 年,下文如不做特殊说明均表示截至到该时间) 人类还未证明 $P \neq NP$ 还是 $P = NP$。
- NPC 类问题 (NP-Complete Problems)
在理解 NPC 类问题之前,我们需要引入如下几个概念:
- 最优化问题 (Optimization Problem) 与 判定问题 (Decision Problem):最优化问题是指问题的每一个可行解都关联一个值,我们希望找到具有最佳值的可行解。判定问题是指问题的答案仅为“是”或“否”的问题。NP 完全性仅适用于判定问题,但通过对最优化问题强加一个界,可以将其转换为判定问题。
- 归约 (Reduction):假设存在一个判定问题 A,该问题的输入称之为实例,我们希望能够在多项式时间内解决该问题。假设存在另一个不同的判定问题 B,并且已知能够在多项式时间内解决该问题,同时假设存在一个过程,它可以将 A 的任何实例
$\alpha$转换成 B 的某个实例$\beta$,转换操作需要在多项式时间内完成,同时两个实例的解是相同的。则我们称这一过程为多项式 规约算法 (Reduction Algorithm)。通过这个过程,我们可以将问题 A 的求解“归约”为对问题 B 的求解,从而利用问题 B 的“易求解性”来证明 A 的“易求解性”。
从而我们可以定义 NPC 类问题为:首先 NPC 类问题是一个 NP 类问题,其次所有的 NP 类问题都可以用多项式时间归约到这类问题。因此,只要找到 NPC 类问题的一个多项式时间的解,则所有的 NP 问题都可以通过多项式时间归约到该问题,并用多项式时间解决该问题,从而使得 $NP = P$,但目前,NPC 类问题并没有找到一个多项式时间的算法。
- NPH 类问题 (NP-Hard Problems)
NPH 类问题定义为所有的 NP 类问题都可以通过多项式时间归约到这类问题,但 NPH 类问题不一定是 NP 类问题。NPH 类问题同样很难找到多项式时间的解,由于 NPH 类问题相比较 NPC 类问题放松了约束,因此即便 NPC 类问题找到了多项式时间的解,NPH 类问题仍可能无法在多项式时间内求解。
下图分别展示了 $P \neq NP$ 和 $P = NP$ 两种假设情况下四类问题之间的关系:
动态规划
动态规划 (Dynamic Programming, DP) 算法通常基于一个递归公式和一个或多个初始状态,并且当前子问题的解可以通过之前的子问题构造出来。动态规划算法求解问题的时间复杂度仅为多项式复杂度,相比其他解法,例如:回溯法,暴利破解法所需的时间要少。动态规划中的 “Programming” 并非表示利用计算机编程,而是一种表格法。动态规划对于每个子问题只求解一次,将解保存在一个表格中,从而避免不必要的重复计算。
动态规划算法的适用情况如下 2:
- 最优子结构性质,即问题的最优解由相关子问题的最优解组合而成,子问题可以独立求解。
- 无后效性,即每个状态均不会影响之前的状态。
- 子问题重叠性质,即在用递归算法自顶向下对问题进行求解时,每次产生的子问题并不总是新问题,有些子问题会被重复计算多次。
一个动态规划算法的核心包含两个部分:状态 和 状态转移方程。状态即一个子问题的表示,同时这个表示需要具备 无后效性。状态转移方程用于描述状态之间的关系,也就是如何利用之前的状态构造出当前的状态进而求解。
动态规划有两种等价的实现方法:
- 带备忘的自顶向下法 (Top-Down with Memoization),该方法采用自然的递归形式编写过程,但会保留每个子问题的解,当需要一个子问题的解时会先检查是否保存过,如果有则直接返回该结果。
- 自底向上法 (Bottom-Up Method),该方法需要恰当的定义子问题“规模”,任何子问题的求解都值依赖于“更小”的子问题的求解,从而可以按照子问题的规模从小到大求解。
两种方法具有相同的渐进运行时间,在某些特殊的情况下,自顶向下的方法并未真正递归地考虑所有可能的子问题;自底向上的方法由于没有频繁的递归调用,时间复杂性函数通常具有更小的系数。
背包问题
背包问题 (Knapsack problem) 是一种组合优化的 NPC 类问题。问题可以描述为:给定一组物品,每种物品都有自己的重量和价值,在限定的总重量内,合理地选择物品使得总价值最高。
形式化的定义,我们有 $n$ 种物品,物品 $j$ 的重量为 $w_j$,价值为 $p_j$,假定所有物品的重量和价值都是非负的,背包所能承受的最大重量为 $W$。如果限定每种物品只能选择 0 个或 1 个,则该问题称为 0-1 背包问题;如果限定物品 $j$ 最多只能选择 $b_j$ 个,则该问题称为 有界背包问题;如果不限定每种物品的数量,则该问题称为 无界背包问题。最优化问题可以表示为:
$$ \begin{equation} \begin{split} \text{maximize} & \sum_{j=1}^{n}{p_j x_j} \\ s.t. & \sum_{j=1}^{n}{w_j x_j} \leq W, x_j \in \left\{0, 1, ..., b_j\right\} \end{split} \end{equation} $$
以 0-1 背包问题为例,用 $d_{i, w}$ 表示取 $i$ 件商品填充一个最大承重 $w$ 的背包的最大价值,问题的最优解即为 $d_{n, W}$。不难写出 0-1 背包问题的状态转移方程如下:
$$ d_{i, w} = \begin{cases} d_{i - 1, w}, & w < w_i \\ \max \left(d_{i - 1, w}, d_{i - 1, w - w_i} + p_i\right), & w \geq w_i \\ 0, & i w = 0 \end{cases} $$
一个 0-1 背包问题的具体示例如下:背包承受的最大重量 $W = 10$,共有 $n = 5$ 种物品,编号分别为 $A, B, C, D, E$,重量分别为 $2, 2, 6, 5, 4$,价值分别为 $6, 3, 5, 4, 6$,利用 BP 求解该问题,不同 $i, w$ 情况下的状态如下表所示 (计算过程详见 这里):
| i \ w | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | NA | (A) 2 - 6 |
(A) 2 - 6 |
(A) 2 - 6 |
(A) 2 - 6 |
(A) 2 - 6 |
(A) 2 - 6 |
(A) 2 - 6 |
(A) 2 - 6 |
(A) 2 - 6 |
| 2 | NA | (A) 2 - 6 |
(A) 2 - 6 |
(A, B) 4 - 9 |
(A, B) 4 - 9 |
(A, B) 4 - 9 |
(A, B) 4 - 9 |
(A, B) 4 - 9 |
(A, B) 4 - 9 |
(A, B) 4 - 9 |
| 3 | NA | (A) 2 - 6 |
(A) 2 - 6 |
(A, B) 4 - 9 |
(A, B) 4 - 9 |
(A, B) 4 - 9 |
(A, B) 4 - 9 |
(A, C) 8 - 11 |
(A, C) 8 - 11 |
(A, B, C) 10 - 14 |
| 4 | NA | (A) 2 - 6 |
(A) 2 - 6 |
(A, B) 4 - 9 |
(A, B) 4 - 9 |
(A, B) 4 - 9 |
(A, D) 7 - 10 |
(A, C) 8 - 11 |
(A, B, D) 9 - 13 |
(A, B, C) 10 - 14 |
| 5 | NA | (A) 2 - 6 |
(A) 2 - 6 |
(A, B) 4 - 9 |
(A, B) 4 - 9 |
(A, E) 6 - 12 |
(A, E) 6 - 12 |
(A, B, E) 8 - 15 |
(A, B, E) 8 - 15 |
(A, B, E) 8 - 15 |
其中,NA 表示未选取任何物品,单元格上部括号中的为选取物品的编号,单元格下部分别为选取物品的总重量和总价值。
最长公共子序列与最长公共子串
给定一个序列 $X = \left\{x_1, x_2, \dotsc, x_m\right\}$,另一个序列 $Z = \left\{z_1, z_2, \dotsc, z_k\right\}$ 在满足如下条件时称其为 $X$ 的一个 子序例 (Subsequence),即存在一个严格递增的 $X$ 的下标序列 $\left\{i_1, i_2, \dotsc, i_k\right\}$,对于所有的 $j = 1, 2, \dotsc, k$,满足 $x_{i_j} = z_j$。给定两个序例 $X$ 和 $Y$,如果 $Z$ 既是 $X$ 的子序列,也是 $Y$ 的子序列,则称它为 $X$ 和 $Y$ 的 公共子序列 (Common Subsequence)。最长公共子序列 (Longest Common Subsequence) 问题为给定两个序列 $X = \left\{x_1, x_2, \dotsc, x_m\right\}$ 和 $Y = \left\{y_1, y_2, \dotsc, y_n\right\}$,求 $X$ 和 $Y$ 最长的公共子序列。
我们可以按如下递归的方式求解最长公共子序列问题:
- 当
$x_i = y_j$时,求解$X = \left\{x_1, x_2, \dotsc, x_{i-1}\right\}$和$Y = \left\{y_1, y_2, \dotsc, y_{j-1}\right\}$的最长公共子序列,在其尾部添加$x_i$和$y_j$即为当前状态下的最长公共子序列。 - 当
$x_i \neq y_j$时,我们则需求解$X = \left\{x_1, x_2, \dotsc, x_{i-1}\right\}$和$Y = \left\{y_1, y_2, \dotsc, y_j\right\}$与$X = \left\{x_1, x_2, \dotsc, x_i\right\}$和$Y = \left\{y_1, y_2, \dotsc, y_{j-1}\right\}$两种情况下最长的公共子序列作为当前状态下的最长公共子序列。
用 $c_{i, j}$ 表示$X = \left\{x_1, x_2, \dotsc, x_i\right\}$ 和 $Y = \left\{y_1, y_2, \dotsc, y_j\right\}$ 情况下的最长公共子序列的长度,则状态转移方程如下:
$$ c_{i, w} = \begin{cases} c_{i - 1, j - 1} + i, & x_i = y_j \\ \max \left(c_{i, j - 1}, c_{i - 1, j}\right), & x_i \neq y_j \\ 0, & i j = 0 \end{cases} $$
例如:给定序列 $X = \left\{A, B, C, B, D, A, B\right\}$ 和序列 $Y = \left\{B, D, C, A, B, A\right\}$,不同状态下最长公共子序列如下表所示 (计算过程详见 这里):
$j$ |
0 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|---|
$i$ |
$y_j$ |
B | D | C | A | B | A | |
| 0 | $x_i$ |
0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | A | 0 | 0 (↑) | 0 (↑) | 0 (↑) | 1 (↖) | 1 (←) | 1 (↖) |
| 2 | B | 0 | 1 (↖) | 1 (←) | 1 (←) | 1 (↑) | 2 (↖) | 2 (←) |
| 3 | C | 0 | 1 (↑) | 1 (↑) | 2 (↖) | 2 (←) | 2 (↑) | 2 (↑) |
| 4 | B | 0 | 1 (↖) | 1 (↑) | 2 (↑) | 2 (↑) | 3 (↖) | 3 (←) |
| 5 | D | 0 | 1 (↑) | 2 (↖) | 2 (↑) | 2 (↑) | 3 (↑) | 3 (↑) |
| 6 | A | 0 | 1 (↑) | 2 (↑) | 2 (↑) | 3 (↖) | 3 (↑) | 4 (↖) |
| 7 | B | 0 | 1 (↖) | 2 (↑) | 2 (↑) | 3 (↑) | 4 (↖) | 4 (↑) |
其中,每个单元格前面的数字为最长公共子序列的长度,后面的符号为还原最长公共子序列使用的备忘录符号。
最长公共子串 (Longest Common Substring) 同最长公共子序列问题略有不同,子序列不要求字符是连续的,而子串要求字符必须是连续的。例如:给定序列 $X = \left\{A, B, C, B, D, A, B\right\}$ 和序列 $Y = \left\{B, D, C, A, B, A\right\}$,最长公共子序列为 $\left\{B, C, B, A\right\}$,而最长公共子串为 $\left\{A, B\right\}$ 或 $\left\{B, D\right\}$。用 $c_{i, j}$ 表示$X = \left\{x_1, x_2, \dotsc, x_i\right\}$ 和 $Y = \left\{y_1, y_2, \dotsc, y_j\right\}$ 情况下的最长公共子串的长度,则状态转移方程如下:
$$ c_{i, w} = \begin{cases} c_{i - 1, j - 1} + i, & x_i = y_j \\ 0, & x_i \neq y_j \\ 0, & i j = 0 \end{cases} $$
利用动态规划可以在 $\Theta \left(nm\right)$ 的时间复杂度内求解,利用广义后缀树 3 可以进一步降低问题求解的时间复杂度 4。
Floyd-Warshall 算法
Floyd-Warshall 算法 是一种求解任意两点之间 最短路 的算法,相比 Dijkstra 算法 5,Floyd-Warshall 算法可以处理有向图或负权图 (但不可以存在负权回路) 的情况 6。
用 $d_{i, j}^{\left(k\right)}$ 表示从 $i$ 到 $j$ 路径上最大节点的标号为 $k$ 的最短路径的长度。有:
$d_{i, j}^{\left(k\right)} = d_{i, k}^{\left(k-1\right)} + d_{k, j}^{\left(k-1\right)}$,若最短路径经过点$k$。$d_{i, j}^{\left(k\right)} = d_{i, j}^{\left(k-1\right)}$,若最短路径不经过点$k$。
则状态转移方程如下:
$$ d_{i, j}^{\left(k\right)} = \begin{cases} w_{i, j}, & k = 0 \\ \min \left(d_{i, j}^{\left(k-1\right)}, d_{i, k}^{\left(k-1\right)} + d_{k, j}^{\left(k-1\right)}\right), & k \leq 1 \end{cases} $$
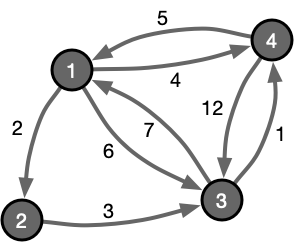
以下图所示的最短路问题为例:
Floyd-Warshall 算法的求解伪代码如下所示:
\begin{algorithm}
\caption{Floyd-Warshall 算法}
\begin{algorithmic}
\REQUIRE \\
边集合 $w$ \\
顶点数量 $c$
\ENSURE \\
距离矩阵 $d$ \\
备忘录矩阵 $m$
\FUNCTION{Floyd-Warshall}{$w, c$}
\FOR{$i$ = $1$ to $c$}
\FOR{$j$ = $1$ to $c$}
\STATE $d_{i, j} \gets \infty$
\ENDFOR
\ENDFOR
\FOR{$i$ = $1$ to $c$}
\STATE $d_{i, i} \gets 0$
\ENDFOR
\FORALL{$w_{i, j}$}
\STATE $d_{i, j} \gets w_{i, j}$
\ENDFOR
\FOR{$k$ = $1$ to $c$}
\FOR{$i$ = $1$ to $c$}
\FOR{$j$ = $1$ to $c$}
\IF{$d_{i, j} > d_{i, k} + d_{k, j}$}
\STATE $d_{i, j} \gets d_{i, k} + d_{k, j}$
\STATE $m_{i, j} \gets k$
\ENDIF
\ENDFOR
\ENDFOR
\ENDFOR
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}
通过备忘录矩阵 $m$,恢复从点 $i$ 到点 $j$ 的过程如下所示:
\begin{algorithm}
\caption{Floyd-Warshall-Path 算法}
\begin{algorithmic}
\REQUIRE \\
备忘录矩阵 $m$ \\
起点 $i$ \\
终点 $j$ \\
路径 $p$
\FUNCTION{Floyd-Warshall-Path}{$m, i, j, p$}
\IF{$i == j$}
\RETURN
\ENDIF
\IF{$m_{i, j} == 0$}
\STATE $p \gets p \cup j$
\ELSE
\STATE Floyd-Warshall-Path($m, i, m_{i, j}, p$)
\STATE Floyd-Warshall-Path($m, m_{i, j}, j, p$)
\ENDIF
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}
文章部分内容参考了 Thomas H. Cormen 等人的《算法导论》
