集成学习算法 (Ensemble Learning)
范叶亮 / 2018-12-08
分类: 机器学习 / 标签: 集成学习, Ensemble Learning, Bagging, Bootstrap Aggregating, Boosting, 模型融合, Averaging, Voting, Stacking, Stacked Generalization, 随机森林, Random Forest, Adaboost, 梯度提升, Gradient Boosting, GBDT, GBM, GBRT, MART, XGBoost, LightGBM, Gradient-based One-Side Sampling, GOSS, Exclusive Feature Bundling, EFB, Level-wise Tree Growth, Depth-wise Tree Growth, Leaf-wise Tree Growth, Best-first Tree Growth, CatBoost / 字数: 10102
传统机器学习算法 (例如:决策树,人工神经网络,支持向量机,朴素贝叶斯等) 的目标都是寻找一个最优分类器尽可能的将训练数据分开。集成学习 (Ensemble Learning) 算法的基本思想就是将多个分类器组合,从而实现一个预测效果更好的集成分类器。集成算法可以说从一方面验证了中国的一句老话:三个臭皮匠,赛过诸葛亮。
Thomas G. Dietterich 1 2 指出了集成算法在统计,计算和表示上的有效原因:
- 统计上的原因
一个学习算法可以理解为在一个假设空间 $\mathcal{H}$ 中选找到一个最好的假设。但是,当训练样本的数据量小到不够用来精确的学习到目标假设时,学习算法可以找到很多满足训练样本的分类器。所以,学习算法选择任何一个分类器都会面临一定错误分类的风险,因此将多个假设集成起来可以降低选择错误分类器的风险。
- 计算上的原因
很多学习算法在进行最优化搜索时很有可能陷入局部最优的错误中,因此对于学习算法而言很难得到一个全局最优的假设。事实上人工神经网络和决策树已经被证实为是一 个NP 问题 3 4。集成算法可以从多个起始点进行局部搜索,从而分散陷入局部最优的风险。
- 表示上的原因
在多数应用场景中,假设空间 $\mathcal{H}$ 中的任意一个假设都无法表示 (或近似表示) 真正的分类函数 $f$。因此,对于不同的假设条件,通过加权的形式可以扩大假设空间,从而学习算法可以在一个无法表示或近似表示真正分类函数 $f$ 的假设空间中找到一个逼近函数 $f$ 的近似值。
集成算法大致可以分为:Bagging,Boosting 和 Stacking 等类型。
Bagging
Bagging (Boostrap Aggregating) 是由 Breiman 于 1996 年提出 5,基本思想如下:
- 每次采用有放回的抽样从训练集中取出
$n$个训练样本组成新的训练集。 - 利用新的训练集,训练得到
$M$个子模型$\{h_1, h_2, ..., h_M\}$。 - 对于分类问题,采用投票的方法,得票最多子模型的分类类别为最终的类别;对于回归问题,采用简单的平均方法得到预测值。
Bagging 算法如下所示:
\begin{algorithm}
\caption{Bagging 算法}
\begin{algorithmic}
\REQUIRE \\
学习算法 $L$ \\
子模型个数 $M$ \\
训练数据集 $T = \{(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)\}$
\ENSURE \\
Bagging 算法 $h_f\left(x\right)$
\FUNCTION{Bagging}{$L, M, T$}
\FOR{$m = 1$ \TO $M$}
\STATE $T_m \gets $ boostrap sample from training set $T$
\STATE $h_m \gets L\left(T_m\right)$
\ENDFOR
\STATE $h_f\left(x\right) \gets \text{sign} \left(\sum_{m=1}^{M} h_m\left(x\right)\right)$
\RETURN $h_f\left(x\right)$
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}
假设对于一个包含 $M$ 个样本的数据集 $T$,利用自助采样,则一个样本始终不被采用的概率是 $\left(1 - \frac{1}{M}\right)^M$,取极限有:
$$ \lim_{x \to \infty} \left(1 - \dfrac{1}{M}\right)^M = \dfrac{1}{e} \approx 0.368 $$
即每个学习器仅用到了训练集中 $63.2\%$ 的数据集,剩余的 $36.8\%$ 的训练集样本可以用作验证集对于学习器的泛化能力进行包外估计 (out-of-bag estimate)。
随机森林 (Random Forests)
随机森林 (Random Forests) 6 是一种利用决策树作为基学习器的 Bagging 集成学习算法。随机森林模型的构建过程如下:
- 数据采样
作为一种 Bagging 集成算法,随机森林同样采用有放回的采样,对于总体训练集 $T$,抽样一个子集 $T_{sub}$ 作为训练样本集。除此之外,假设训练集的特征个数为 $d$,每次仅选择 $k\left(k < d\right)$ 个构建决策树。因此,随机森林除了能够做到样本扰动外,还添加了特征扰动,对于特征的选择个数,推荐值为 $k = \log_2 d$ 6。
- 树的构建
每次根据采样得到的数据和特征构建一棵决策树。在构建决策树的过程中,会让决策树生长完全而不进行剪枝。构建出的若干棵决策树则组成了最终的随机森林。
随机森林在众多分类算法中表现十分出众 7,其主要的优点包括:
- 由于随机森林引入了样本扰动和特征扰动,从而很大程度上提高了模型的泛化能力,尽可能地避免了过拟合现象的出现。
- 随机森林可以处理高维数据,无需进行特征选择,在训练过程中可以得出不同特征对模型的重要性程度。
- 随机森林的每个基分类器采用决策树,方法简单且容易实现。同时每个基分类器之间没有相互依赖关系,整个算法易并行化。
Boosting
Boosting 是一种提升算法,可以将弱的学习算法提升 (boost) 为强的学习算法。基本思路如下:
- 利用初始训练样本集训练得到一个基学习器。
- 提高被基学习器误分的样本的权重,使得那些被错误分类的样本在下一轮训练中可以得到更大的关注,利用调整后的样本训练得到下一个基学习器。
- 重复上述步骤,直至得到
$M$个学习器。 - 对于分类问题,采用有权重的投票方式;对于回归问题,采用加权平均得到预测值。
Adaboost
Adaboost 8 是 Boosting 算法中有代表性的一个。原始的 Adaboost 算法用于解决二分类问题,因此对于一个训练集
$$ T = \{\left(x_1, y_1\right), \left(x_2, y_2\right), ..., \left(x_n, y_n\right)\} $$
其中 $x_i \in \mathcal{X} \subseteq \mathbb{R}^n, y_i \in \mathcal{Y} = \{-1, +1\}$,首先初始化训练集的权重
$$ \begin{equation} \begin{split} D_1 =& \left(w_{11}, w_{12}, ..., w_{1n}\right) \\ w_{1i} =& \dfrac{1}{n}, i = 1, 2, ..., n \end{split} \end{equation} $$
根据每一轮训练集的权重 $D_m$,对训练集数据进行抽样得到 $T_m$,再根据 $T_m$ 训练得到每一轮的基学习器 $h_m$。通过计算可以得出基学习器 $h_m$ 的误差为 $\epsilon_m$,根据基学习器的误差计算得出该基学习器在最终学习器中的权重系数
$$ \alpha_m = \dfrac{1}{2} \ln \dfrac{1 - \epsilon_m}{\epsilon_m} $$
更新训练集的权重
$$ \begin{equation} \begin{split} D_{m+1} =& \left(w_{m+1, 1}, w_{m+1, 2}, ..., w_{m+1, n}\right) \\ w_{m+1, i} =& \dfrac{w_{m, i}}{Z_m} \exp \left(-\alpha_m y_i h_m\left(x_i\right)\right) \end{split} \end{equation} $$
其中 $Z_m$ 为规范化因子
$$ Z_m = \sum_{i = 1}^{n} w_{m, i} \exp \left(-\alpha_m y_i h_m \left(x_i\right)\right) $$
从而保证 $D_{m+1}$ 为一个概率分布。最终根据构建的 $M$ 个基学习器得到最终的学习器:
$$ h_f\left(x\right) = \text{sign} \left(\sum_{m=1}^{M} \alpha_m h_m\left(x\right)\right) $$
AdaBoost 算法过程如下所示:
\begin{algorithm}
\caption{AdaBoost 算法}
\begin{algorithmic}
\REQUIRE \\
学习算法 $L$ \\
子模型个数 $M$ \\
训练数据集 $T = \{(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)\}$
\ENSURE \\
AdaBoost 算法 $h_f\left(x\right)$
\FUNCTION{AdaBoost}{$L, M, T$}
\STATE $D_1\left(x\right) \gets 1 / n$
\FOR{$m = 1$ \TO $M$}
\STATE $T_{sub} \gets $ sample from training set $T$ with weights
\STATE $h_m \gets L\left(T_{sub}\right)$
\STATE $\epsilon_m\gets Error\left(h_m\right)$
\IF{$\epsilon_m > 0.5$}
\BREAK
\ENDIF
\STATE $\alpha_m \gets \dfrac{1}{2} \ln \dfrac{1 - \epsilon_m}{\epsilon_m}$
\STATE $D_{m+1} \gets \dfrac{D_m \exp \left(-\alpha_m y h_m\left(x\right)\right)}{Z_m}$
\ENDFOR
\STATE $h_f\left(x\right) \gets \text{sign} \left(\sum_{m=1}^{M} \alpha_m h_m\left(x\right)\right)$
\RETURN $h_f\left(x\right)$
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}
GBDT (GBM, GBRT, MART)
GBDT (Gradient Boosting Decision Tree) 是另一种基于 Boosting 思想的集成算法,除此之外 GBDT 还有很多其他的叫法,例如:GBM (Gradient Boosting Machine),GBRT (Gradient Boosting Regression Tree),MART (Multiple Additive Regression Tree) 等等。GBDT 算法由 3 个主要概念构成:Gradient Boosting (GB),Regression Decision Tree (DT 或 RT) 和 Shrinkage。
从 GBDT 的众多别名中可以看出,GBDT 中使用的决策树并非我们最常用的分类树,而是回归树。分类树主要用于处理响应变量为因子型的数据,例如天气 (可以为晴,阴或下雨等)。回归树主要用于处理响应变量为数值型的数据,例如商品的价格。当然回归树也可以用于二分类问题,对于回归树预测出的数值结果,通过设置一个阈值即可以将数值型的预测结果映射到二分类问题标签上,即 $\mathcal{Y} = \{-1, +1\}$。
对于 Gradient Boosting 而言,首先,Boosting 并不是 Adaboost 中 Boost 的概念,也不是 Random Forest 中的重抽样。在 Adaboost 中,Boost 是指在生成每个新的基学习器时,根据上一轮基学习器分类对错对训练集设置不同的权重,使得在上一轮中分类错误的样本在生成新的基学习器时更被重视。GBDT 中在应用 Boost 概念时,每一轮所使用的数据集没有经过重抽样,也没有更新样本的权重,而是每一轮选择了不用的回归目标,即上一轮计算得到的残差 (Residual)。其次,Gradient 是指在新一轮中在残差减少的梯度 (Gradient) 上建立新的基学习器。
下面我们通过一个年龄预测的 示例 (较之原示例有修改) 简单介绍 GBDT 的工作流程。
假设存在 4 个人 $P = \{p_1, p_2, p_3, p_4\}$,他们的年龄分别为 $14, 16, 24, 26$。其中 $p_1, p_2$ 分别是高一和高三学生,$p_3, p_4$ 分别是应届毕业生和工作两年的员工。利用原始的决策树模型进行训练可以得到如下图所示的结果:
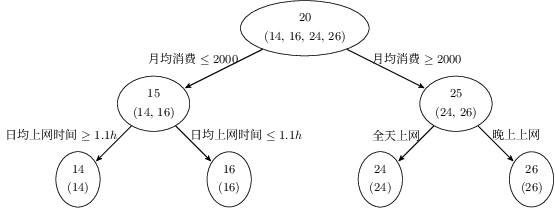
利用 GBDT 训练模型,由于数据量少,在此我们限定每个基学习器中的叶子节点最多为 2 个,即树的深度最大为 1 层。训练得到的结果如下图所示:

在训练第一棵树过程中,利用年龄作为预测值,根据计算可得由于 $p_1, p_2$ 年龄相近,$p_3, p_4$ 年龄相近被划分为两组。通过计算两组中真实年龄和预测的年龄的差值,可以得到第一棵树的残差 $R = \{-1, 1, -1, 1\}$。因此在训练第二棵树的过程中,利用第一棵树的残差作为标签值,最终所有人的年龄均正确被预测,即最终的残差均为 $0$。
则对于训练集中的 4 个人,利用训练得到的 GBDT 模型进行预测,结果如下:
$p_1$:14 岁高一学生。购物较少,经常问学长问题,预测年龄$Age = 15 - 1 = 14$。$p_2$:16 岁高三学生。购物较少,经常回答学弟问题,预测年龄$Age = 15 + 1 = 16$。$p_3$:24 岁应届毕业生。购物较多,经常问别人问题,预测年龄$Age = 25 - 1 = 24$。$p_4$:26 岁 2 年工作经验员工。购物较多,经常回答别人问题,预测年龄$Age = 25 + 1 = 26$。
整个 GBDT 算法流程如下所示:
\begin{algorithm}
\caption{GBDT 算法}
\begin{algorithmic}
\REQUIRE \\
子模型个数 $M$ \\
训练数据集 $T = \{(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)\}$
\ENSURE \\
GBDT 算法 $h_f\left(x\right)$
\FUNCTION{GBDT}{$M, T$}
\STATE $F_1\left(x\right) \gets \sum_{i = 1}^{N} y_i / N$
\FOR{$m = 1$ \TO $M$}
\STATE $r_m \gets y - F_m \left(x\right)$
\STATE $T_m \gets \left(x, r_m\right)$
\STATE $h_m \gets RegressionTree \left(T_m\right)$
\STATE $\alpha_m \gets \dfrac{\sum_{i = 1}^{N} r_{im} h_m \left(x_i\right)}{\sum_{i = 1}^{N} h_m \left(x_i\right)^2}$
\STATE $F_m \left(x\right) = F_{m-1} \left(x\right) + \alpha_m h_m \left(x\right)$
\ENDFOR
\STATE $h_f\left(x\right) = F_M \left(x\right)$
\RETURN $h_f\left(x\right)$
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}
GBDT 中也应用到了 Shrinkage 的思想,其基本思想可以理解为每一轮利用残差学习得到的回归树仅学习到了一部分知识,因此我们无法完全信任一棵树的结果。Shrinkage 思想认为在新的一轮学习中,不能利用全部残差训练模型,而是仅利用其中一部分,即:
$$ r_m = y - s F_m \left(x\right), 0 \leq s \leq 1 $$
注意,这里的 Shrinkage 和学习算法中 Gradient 的步长是两个不一样的概念。Shrinkage 设置小一些可以避免发生过拟合现象;而 Gradient 中的步长如果设置太小则会陷入局部最优,如果设置过大又容易结果不收敛。
XGBoost
XGBoost 是由 Chen 等人 9 提出的一种梯度提升树模型框架。XGBoost 的基本思想同 GBDT 一样,对于一个包含 $n$ 个样本和 $m$ 个特征的数据集 $\mathcal{D} = \left\{\left(\mathbf{x}_i, y_i\right)\right\}$,其中 $\left|\mathcal{D}\right| = n, \mathbf{x}_i \in \mathbb{R}^m, y_i \in \mathbb{R}$,一个集成树模型可以用 $K$ 个加法函数预测输出:
$$ \hat{y}_i = \phi \left(\mathbf{x}_i\right) = \sum_{k=1}^{K}{f_k \left(\mathbf{x}_i\right)}, f_k \in \mathcal{F} $$
其中,$\mathcal{F} = \left\{f \left(\mathbf{x}\right) = w_{q \left(\mathbf{x}\right)}\right\} \left(q: \mathbb{R}^m \to T, w \in \mathbb{R}^T\right)$ 为回归树 (CART),$q$ 表示每棵树的结构,其将一个样本映射到最终的叶子节点,$T$ 为叶子节点的数量,每个 $f_w$ 单独的对应一棵结构为 $q$ 和权重为 $w$ 的树。不同于决策树,每棵回归树的每个叶子节点上包含了一个连续的分值,我们用 $w_i$ 表示第 $i$ 个叶子节点上的分值。
XGBoost 首先对损失函数进行了改进,添加了 L2 正则项,同时进行了二阶泰勒展开。损失函数表示为:
$$ \begin{equation} \begin{split} \mathcal{L} \left(\phi\right) = \sum_{i}{l \left(\hat{y}_i, y_i\right)} + \sum_{k}{\Omega \left(f_k\right)} \\ \text{where} \ \Omega \left(f\right) = \gamma T + \dfrac{1}{2} \lambda \left\| w \right\|^2 \end{split} \end{equation} $$
其中,$l$ 为衡量预测值 $\hat{y}_i$ 和真实值 $y_i$ 之间差异的函数,$\Omega$ 为惩罚项,$\gamma$ 和 $\lambda$ 为惩罚项系数。
我们用 $\hat{y}_i^{\left(t\right)}$ 表示第 $t$ 次迭代的第 $i$ 个实例,我们需要增加 $f_t$ 来最小化如下的损失函数:
$$ \mathcal{L}^{\left(t\right)} = \sum_{i=1}^{n}{l \left(y_i, \hat{y}_i^{\left(t-1\right)} + f_t \left(\mathbf{x}_i\right)\right)} + \Omega \left(f_t\right) $$
对上式进行二阶泰勒展开有:
$$ \mathcal{L}^{\left(t\right)} \simeq \sum_{i=1}^{n}{\left[l \left(y_i, \hat{y}_i^{\left(t-1\right)}\right) + g_i f_t \left(\mathbf{x}_i\right) + \dfrac{1}{2} h_i f_t^2 \left(\mathbf{x}_i\right)\right]} + \Omega \left(f_t\right) $$
其中,$g_i = \partial_{\hat{y}^{\left(t-1\right)}} l \left(y_i, \hat{y}^{\left(t-1\right)}\right), h_i = \partial_{\hat{y}^{\left(t-1\right)}}^{2} l \left(y_i, \hat{y}^{\left(t-1\right)}\right)$ 分别为损失函数的一阶梯度和二阶梯度。去掉常数项,第 $t$ 步的损失函数可以简化为:
$$ \tilde{\mathcal{L}}^{\left(t\right)} = \sum_{i=1}^{n}{\left[ g_i f_t \left(\mathbf{x}_i\right) + \dfrac{1}{2} h_i f_t^2 \left(\mathbf{x}_i\right)\right]} + \Omega \left(f_t\right) $$
令 $I_j = \left\{i \ | \ q \left(\mathbf{x}_i\right) = j\right\}$ 表示叶子节点 $j$ 的实例集合,上式可重写为:
$$ \begin{equation} \begin{split} \tilde{\mathcal{L}}^{\left(t\right)} &= \sum_{i=1}^{n}{\left[ g_i f_t \left(\mathbf{x}_i\right) + \dfrac{1}{2} h_i f_t^2 \left(\mathbf{x}_i\right)\right]} + \gamma T + \dfrac{1}{2} \lambda \sum_{j=1}^{T}{w_j^2} \\ &= \sum_{j=1}^{T}{\left[\left(\sum_{i \in I_j}{g_i}\right) w_j + \dfrac{1}{2} \left(\sum_{i \in I_j}{h_i + \lambda}\right) w_j^2\right]} + \gamma T \end{split} \end{equation} $$
对于一个固定的结构 $q \left(\mathbf{x}\right)$,可以通过下式计算叶子节点 $j$ 的最优权重 $w_j^*$:
$$ w_j^* = - \dfrac{\sum_{i \in I_j}{g_i}}{\sum_{i \in I_j}{h_i} + \lambda} $$
进而计算对应的最优值:
$$ \tilde{\mathcal{L}}^{\left(t\right)} \left(q\right) = - \dfrac{1}{2} \sum_{j=1}^{T}{\dfrac{\left(\sum_{i \in I_j}{g_i}\right)^2}{\sum_{i \in I_j}{h_i} + \lambda}} + \gamma T $$
上式可以作为评价树的结构 $q$ 的评分函数。通常情况下很难枚举所有可能的树结构,一个贪心的算法是从一个节点出发,逐层的选择最佳的分裂节点。令 $I_L$ 和 $I_R$ 分别表示分裂后左侧和右侧的节点集合,令 $I = I_L \cup I_R$,则分裂后损失的减少量为:
$$ \mathcal{L}_{\text{split}} = \dfrac{1}{2} \left[\dfrac{\left(\sum_{i \in I_L}{g_i}\right)^2}{\sum_{i \in I_L}{h_i} + \lambda} + \dfrac{\left(\sum_{i \in I_R}{g_i}\right)^2}{\sum_{i \in I_R}{h_i} + \lambda} - \dfrac{\left(\sum_{i \in I}{g_i}\right)^2}{\sum_{i \in I}{h_i} + \lambda}\right] - \gamma $$
XGBoost 也采用了 Shrinkage 的思想减少每棵树的影响,为后续树模型留下更多的改进空间。同时 XGBoost 也采用了随机森林中的特征下采样 (列采样) 方法用于避免过拟合,同时 XGBoost 也支持样本下采样 (行采样)。XGBoost 在分裂点的查找上也进行了优化,使之能够处理无法将全部数据读入内存的情况,同时能够更好的应对一些由于数据缺失,大量零值和 One-Hot 编码导致的特征稀疏问题。除此之外,XGBoost 在系统实现,包括:并行化,Cache-Aware 加速和数据的核外计算 (Out-of-Core Computation) 等方面也进行了大量优化,相关具体实现请参见论文和 文档。
LightGBM
LightGBM 是由微软研究院的 Ke 等人 10 提出了一种梯度提升树模型框架。之前的 GBDT 模型在查找最优分裂点时需要扫描所有的样本计算信息增益,因此其计算复杂度与样本的数量和特征的数量成正比,这使得在处理大数据量的问题时非常耗时。LightGBM 针对这个问题提出了两个算法:
- Gradient-based One-Side Sampling (GOSS)
- Exclusive Feature Bundling (EFB)
Gradient-based One-Side Sampling
在 AdaBoost 中,样本的权重很好的诠释了数据的重要性,但在 GBDT 中并没有这样的权重,因此无法直接应用 AdaBoost 的采样方法。幸运的是 GBDT 中每个样本的梯度可以为我们的数据采样提供有用的信息。当一个样本具有较小的梯度时,其训练的误差也较小,表明其已经训练好了。一个直观的想法就是丢弃这些具有较小梯度的样本,但是这样操作会影响整个数据的分布,从而对模型的精度造成损失。
GOSS 的做法是保留具有较大梯度的样本,并从具有较小梯度的样本中随机采样。同时为了补偿对数据分布的影响,在计算信息增益的时候,GOSS 针对梯度较小的样本引入了一个常数乘子。这样就保证了模型更多的关注未得到较好训练的数据,同时又不会对原始数据分布改变过多。整个算法流程如下:
\begin{algorithm}
\caption{GOSS 算法}
\begin{algorithmic}
\INPUT \\
训练数据 $I$ \\
迭代次数 $d$ \\
具有较大梯度数据的采样比例 $a$ \\
具有较小梯度数据的采样比例 $b$ \\
损失函数 $loss$ \\
基学习器 $L$
\FUNCTION{GOSS}{$I, d, a, b, loss, L$}
\STATE $\text{models} \gets \varnothing$
\STATE $\text{fact} \gets \dfrac{1-a}{b}$
\STATE $\text{topN} \gets a \times \text{len} \left(I\right)$
\STATE $\text{randN} \gets b \times \text{len} \left(I\right)$
\FOR{$i = 1$ \TO $d$}
\STATE $\text{preds} \gets \text{models.predict} \left(I\right)$
\STATE $\text{g} \gets loss \left(I, \text{preds}\right)$
\STATE $\text{w} \gets \left\{1, 1, \dotsc\right\}$
\STATE $\text{sorted} \gets \text{GetSortedIndices} \left(\text{abs} \left(\text{g}\right)\right)$
\STATE $\text{topSet} \gets \text{sorted[1:topN]}$
\STATE $\text{randSet} \gets \text{RandomPick} \left(\text{sorted[topN:len}\left(I\right)\text{]}, \text{randN}\right)$
\STATE $\text{usedSet} \gets \text{topSet} \cup \text{randSet}$
\STATE $\text{w[randSet]} \gets \text{w[randSet]} \times \text{fact}$
\STATE $\text{newModel} \gets L \left(I \text{[usedSet]}, - \text{g[usedSet]}, \text{w[usedSet]}\right)$
\STATE $\text{models} \gets \text{models} \cup \text{newModel}$
\ENDFOR
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}
Exclusive Feature Bundling
高维数据往往是稀疏的,特征空间的稀疏性为我们提供了可能的近似无损的特征降维实现。进一步而言,在稀疏的特征空间中,很多特征之间是互斥的,也就是说它们不同时取非零值。因此,我们就可以将这些互斥的特征绑定成一个特征。由于 $\#bundle \ll \#feature$,因此构建直方图的复杂度就可以从 $O \left(\#data \times \#features\right)$ 减小至 $O \left(\#data \times \#bundle\right)$,从而在不损失精度的情况下加速模型的训练。这样我们就需要解决如下两个问题:
- 确定对哪些特征进行绑定。
- 如果对这些特征进行绑定。
对哪些特征进行绑定可以利用 图着色问题 进行解决。对于一个图 $G = \left(V, E\right)$,将 $G$ 的 关联矩阵 中的每一行看成特征,得到 $|V|$ 个特征,从而可以得出图中颜色相同的节点即为互斥的特征。算法如下:
\begin{algorithm}
\caption{Greedy Bundling}
\begin{algorithmic}
\INPUT \\
特征 $F$ \\
最大冲突数量 $K$
\OUTPUT \\
需要绑定的特征 $bundles$
\FUNCTION{GreedyBundling}{$F, K$}
\STATE Construct graph $G$
\STATE $\text{searchOrder} \gets G.\text{sortByDegree}()$
\STATE $\text{bundles} \gets \varnothing$
\STATE $\text{bundlesConflict} \gets \varnothing$
\FOR{$i$ $\in$ searchOrder}
\STATE $\text{needNew} \gets$ \TRUE
\FOR{$j = 1$ \TO len(bundles)}
\STATE $\text{cnt} \gets$ ConflictCnt(bundles[$j$],F[$i$])
\IF{cnt $+$ bundlesConflict[$i$] $\leq K$}
\STATE bundles[$j$].add($F[i]$)
\STATE $\text{needNew} \gets$ \FALSE
\BREAK
\ENDIF
\ENDFOR
\IF{needNew}
\STATE $bundles \gets bundles \cup F[i]$
\ENDIF
\ENDFOR
\RETURN $bundles$
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}
上述算法的复杂度为 $O \left(\#feature^2\right)$ ,并且仅在模型训练前运行一次。对于特征数不是很大的情况是可以接受的,但当特征数量很大时算法效率并不令人满意。进一步的优化是在不构造图的情况下进行高效的排序,即根据非零值的数量进行排序,更多的非零值意味着更高的冲突概率。
合并特征的关键在于确保原始特征的值能够从合并后的特征之中识别出来。由于基于直方图的算法保存的是原始特征的离散桶,而非连续的值,因此我们可以将互斥的特征置于不同的桶内。算法如下:
\begin{algorithm}
\caption{Merge Exclusive Features}
\begin{algorithmic}
\REQUIRE \\
数据数量 $numData$ \\
一组互斥特征 $F$
\ENSURE \\
新的分箱 $newBin$ \\
分箱范围 $binRanges$
\FUNCTION{MergeExclusiveFeatures}{$numData, F$}
\STATE $\text{binRages} \gets \left\{0\right\}$
\STATE $\text{totalBin} \gets 0$
\FOR{$f$ $\in$ $F$}
\STATE $\text{totalBin} \gets \text{totalBin} + \text{f.numBin}$
\STATE $\text{binRanges} \gets \text{binRanges} \cup \text{totalBin}$
\ENDFOR
\STATE $\text{newBin} \gets \text{Bin} \left(numData\right)$
\FOR{$i = 1$ \TO $numData$}
\STATE $\text{newBin}[i] \gets 0$
\FOR{$j = 1$ \TO $\text{len} \left(F\right)$}
\IF{$F[j].\text{bin}[i] \neq 0$}
\STATE $\text{newBin}[i] \gets F[j].\text{bin}[i] + \text{binRanges}[j]$
\ENDIF
\ENDFOR
\ENDFOR
\RETURN $newBin, binRanges$
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}
EFB 算法可以将大量的互斥特征合并为少量的稠密特征,从而通过避免对零值特征的计算提高算法的运行效率。
Tree Growth
大多的决策树算法通过逐层 (Level-wise / Depth-wise) 的方法生成树,如下图所示:

LightGBM 采用了另外一种 Leaf-wise (或称 Best-first) 的方式生成 11,如下图所示:

该方法想选择具有最大 Delta Loss 值的叶子节点进行生长。在固定叶子节点数量的情况下,Leaf-wise 的生长方式比 Level-wise 的方式更容易获得较低的损失值。Leaf-wise 的生长方式在数据量较小时容易产生过拟合的现象,在 LightGBM 中可以通过限制树的最大深度减轻该问题。
更多有关 LightGBM 的优化请参见论文和 文档。
CatBoost
CatBoost 是由俄罗斯 Yandex 公司 12 13 提出的一种梯度提升树模型框架。相比于之前的实现,CatBoost 的优化主要包括如下几点:
- 提出了一种处理分类特征 (Categorical Features) 的算法。
- 提出了一种解决预测偏移 (Prediction Shift) 问题的算法。
分类特征
分类特征是由一些离散的值构成的集合,其无法直接应用在提升树模型中,一个常用的方法是利用 One-Hot 编码对分类特征进行预处理,将其转化成值特征。
另一种方法是根据样本的标签值计算分类特征的一些统计量 (Target Statistics, TS)。令 $\mathcal{D} = \left\{\left(\mathbf{x}_k, y_k\right)\right\}_{k=1, \dotsc, n}$ 为一个数据集,其中 $\mathbf{x}_k = \left(x_k^1, \dotsc, x_k^m\right)$ 为一个包含 $m$ 个特征的向量 (包含值特征和分类特征),$y_k \in \mathbb{R}$ 为标签值。最简单的做法是将分类特征替换为全量训练数据上对应特征值相同的标签值的均值,即 $\hat{x}_k^i \approx \mathbb{E} \left(y \ | \ x^i = x_k^i\right)$。
- Greedy TS
一个简单估计 $\mathbb{E} \left(y \ | \ x^i = x_k^i\right)$ 的方法是对具有相同类型 $x_k^i$ 的样本的标签值求均值。但这种估计对于低频的分类噪音较大,因此我们可以通过一个先验 $P$ 来进行平滑:
$$ \hat{x}_k^i = \dfrac{\sum_{j=1}^{n}{\boldsymbol{1}_{\left\{x_j^i = x_k^i\right\}} \cdot y_j} + a P}{\sum_{j=1}^{n}{\boldsymbol{1}_{\left\{x_j^i = x_k^i\right\}}} + a} $$
其中,$a > 0$ 为先验系数,$\boldsymbol{1}$ 为指示函数,通常 $P$ 取整个数据集标签值的均值。
上述贪婪 (Greedy) 的做法的问题在于存在目标泄露 (Target Leakage),即特征 $\hat{x}_k^i$ 是通过 $\mathbf{x}_k$ 的目标 $y_k$ 计算所得。这会导致条件偏移 (Conditional Shift) 的问题 14,即 $\hat{x}^i \ | \ y$ 的分布在训练集和测试集上不同。因此在计算 TS 时需要满足如下特性:
一种修正方法是在计算 TS 时使用排除掉 $\mathbf{x}_k$ 的一个子集,令 $\mathcal{D}_k \subset \mathcal{D} \setminus \left\{\mathbf{x}_k\right\}$,有:
$$ \hat{x}_k^i = \dfrac{\sum_{\mathbf{x}_j \in \mathcal{D}_k}{\boldsymbol{1}_{\left\{x_j^i = x_k^i\right\}} \cdot y_j} + a P}{\sum_{\mathbf{x}_j \in \mathcal{D}_k}{\boldsymbol{1}_{\left\{x_j^i = x_k^i\right\}}} + a} $$
- Holdout TS
另一种方法是将训练集划分为两部分 $\mathcal{D} = \hat{\mathcal{D}}_0 \sqcup \hat{\mathcal{D}_1}$,利用 $\mathcal{D}_k = \hat{\mathcal{D}}_0$ 计算 TS,利用 $\hat{\mathcal{D}_1}$ 进行训练。虽然满足了 特性 1,但是这会导致计算 TS 和用于训练的数据均显著减少,因此还需要满足另一个特性:
- Leave-one-out TS
对于训练样本 $\mathbf{x}_k$ 令 $\mathcal{D}_k = \mathcal{D} \setminus \mathbf{x}_k$,对于测试集,令 $\mathcal{D}_k = \mathcal{D}$,但这并没有解决 Target Leakage 问题。
- Ordered TS
Catboost 采用了一种更有效的策略:首先对于训练样本进行随机排列,得到排列下标 $\sigma$,之后对于每个训练样本仅利用“历史”样本来计算 TS,即:$\mathcal{D}_k = \left\{\mathbf{x}_j: \sigma \left(j\right) < \sigma \left(k\right)\right\}$,对于每个测试样本 $\mathcal{D}_k = \mathcal{D}$。
Prediction Shift & Ordered Boosting
类似计算 TS,Prediction Shift 是由一种特殊的 Target Leakage 所导致的。对于第 $t$ 次迭代,我们优化的目标为:
$$ h^t = \mathop{\arg\min}_{h \in H} \mathbb{E} \left(-g^t \left(\mathbf{x}, y\right) - h \left(\mathbf{x}\right)\right)^2 \label{eq:catboost-obj} $$
其中,$g^t \left(\mathbf{x}, y\right) := \dfrac{\partial L \left(y, s\right)}{\partial s} \bigg\vert_{s = F^{t-1} \left(\mathbf{x}\right)}$。通常情况下会使用相同的数据集 $\mathcal{D}$ 进行估计:
$$ h^t = \mathop{\arg\min}_{h \in H} \dfrac{1}{n} \sum_{k=1}^{n}{\left(-g^t \left(\mathbf{x}_k, y_k\right) - h \left(\mathbf{x}_k\right)\right)^2} \label{eq:catboost-obj-approx} $$
整个偏移的链条如下:
- 梯度的条件分布
$g^t \left(\mathbf{x}_k, y_k\right) \ | \ \mathbf{x}_k$同测试样本对应的分布$g^t \left(\mathbf{x}, y\right) \ | \ \mathbf{x}$存在偏移。 - 由式
$\ref{eq:catboost-obj}$定义的基学习器$h^t$同由式$\ref{eq:catboost-obj-approx}$定义的估计方法存在偏移。 - 最终影响训练模型
$F^t$的泛化能力。
每一步梯度的估计所使用的标签值同构建当前模型 $F^{t-1}$ 使用的相同。但是,对于一个训练样本 $\mathbf{x}_k$ 而言,条件分布 $F^{t-1} \left(\mathbf{x}_k \ | \ \mathbf{x}_k\right)$ 相对一个测试样本 $\mathbf{x}$ 对应的分布 $F^{t-1} \left(\mathbf{x}\right) \ | \ \mathbf{x}$ 发生了偏移,我们称这为预测偏移 (Prediction Shift)。
CatBoost 提出了一种解决 Prediction Shift 的算法:Ordered Boosting。假设对于训练数据进行随机排序得到 $\sigma$,并有 $n$ 个不同的模型 $M_1, \dotsc, M_n$,每个模型 $M_i$ 仅利用随机排序后的前 $i$ 个样本训练得到。算法如下:
\begin{algorithm}
\caption{Ordered Boosting}
\begin{algorithmic}
\INPUT \\
训练集 $\left\{\left(\mathbf{x}_k, y_k\right)\right\}_{k=1}^{n}$ \\
树的个数 $I$
\OUTPUT \\
模型 $M_n$
\FUNCTION{OrderedBoosting}{$numData, F$}
\STATE $\sigma \gets \text{random permutation of} \left[1, n\right]$
\STATE $M_i \gets 0$ for $i = 1, \dotsc, n$
\FOR{$t = 1$ \TO $I$}
\FOR{$i = 1$ \TO $n$}
\STATE $r_i \gets y_i - M_{\sigma \left(i\right) -1} \left(\mathbf{x}_i\right)$
\ENDFOR
\FOR{$i = 1$ \TO $n$}
\STATE $\Delta M \gets \text{LearnModel} \left(\left(\mathbf{x}_j, r_j\right): \sigma \left(j\right) \leq i\right)$
\STATE $M_i \gets M_i + \Delta M$
\ENDFOR
\ENDFOR
\RETURN $M_n$
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}
在计算 TS 和进行 Ordered Boosting 时我们均使用了随机排列并得到 $\sigma_{cat}$ 和 $\sigma_{boost}$。需要注意的是在将两部分合并为一个算法时,我们需要令 $\sigma_{cat} = \sigma_{boost}$ 避免 Prediction Shift。这样可以保证目标 $y_i$ 不用于训练模型 $M_i$ (既不参与计算 TS,也不用于梯度估计)。
更多 CatBoost 的实现细节请参见论文和 文档。
不同实现的比较
针对 scikit-learn,XGBoost,LightGBM 和 CatBoost 4 种 GBDT 的具体实现,下表汇总了各自的相关特性:
| scikit-learn | XGBoost | LightGBM | CatBoost | |
|---|---|---|---|---|
| 当前版本 | 0.20.1 | 0.81 | 2.2.2 | 0.11.1 |
| 实现语言 | C, C++, Python | C, C++ | C, C++ | C++ |
| API 语言 | Python | Python, R, Java, Scala, C++ and more | Python, R | Python, R |
| 模型导出 | JPMML 15 | JPMML 16, ONNX 17 18 | ONNX 17 19 | CoreML, Python, C++, JSON 20 |
| 多线程 | No | Yes | Yes | Yes |
| GPU | No | Yes 21 | Yes 22 | Yes 23 |
| 多 GPU | No | Yes 21 | No | Yes 23 |
| Boosting 类型 | Gradient Boosted Tree (GBDT) | GBDT (booster: gbtree) Generalized Linear Model, GLM (booster: gbliner) Dropout Additive Regression Tree, DART (booster: dart) |
GBDT (boosting: gbdt) Random Forest (boosting: rf) DART (boosting: dart) Gradient-based One-Side Sampling, GOSS (bossting: goss) |
Ordered (boosting_type: Ordered) Plain (bossting_type: Plain) |
| Level-wise (Depth-wise) Split | Yes | Yes (grow_policy: depthwise) |
No | Yes |
| Leaf-wise (Best-first) Split | No | Yes (grow_policy: lossguide) |
Yes | No |
| Histogram-based Split | No | Yes (tree_method: hist / gpu_hist) |
Yes | Yes |
| 过拟合控制 | Yes (max_depth, …) |
Yes (max_depth, max_leaves, gamma, reg_alpha, reg_lamda, …) |
Yes (max_depth, num_leaves, gamma, reg_alpha, reg_lamda, drop_rate, …) |
Yes (max_depth, reg_lambda, …) |
| 分类特征 | No | No | Yes (categorical_feature) |
Yes (cat_features) |
| 缺失值处理 | No | Yes | Yes (use_missing) |
Yes |
| 不均衡数据 | No | Yes (scale_pos_weight, max_delta_step) |
Yes (scale_pos_weight, poisson_max_delta_step) |
Yes (scale_pos_weight) |
不同实现的性能分析和比较可参见如下文章,括号中内容为分析的实现库:
- GPU Accelerated XGBoost (XGBoost)
- Updates to the XGBoost GPU algorithms (XGBoost)
- LightGBM Experiments (XGBoost, LightGBM),代码
- GPU Tunning Guide and Performance Comparision (LightGBM)
- Lessons Learned From Benchmarking Fast Machine Learning Algorithms (XGBoost, LightGBM), 代码
- CatBoost Benchmarks (XGBoost, LightGBM, CatBoost, H2O)
- Benchmarking and Optimization of Gradient Boosted Decision Tree Algorithms (XGBoost, LightGBM, CatBoost)
- Laurae++: xgboost / LightGBM (XGBoost, LightGBM), 代码
- GBM Performance (XGBoost, LightGBM, H2O), 代码
Stacking
Stacking 本身是一种集成学习方法,同时也是一种模型组合策略,我们首先介绍一些相对简单的模型组合策略:平均法 和 投票法。
对于 数值型的输出 $h_i \left(\mathbf{x}\right) \in \mathbb{R}$,
- 简单平均法 (Simple Averaging)
$$ H \left(\mathbf{x}\right) = \dfrac{1}{M} \sum_{i=1}^{M}{h_i \left(\mathbf{x}\right)} $$
- 加权平均法 (Weighted Averaging)
$$ H \left(\mathbf{x}\right) = \sum_{i=1}^{M}{w_i h_i \left(\mathbf{x}\right)} $$
其中,$w_i$ 为学习器 $h_i$ 的权重,且 $w_i \geq 0, \sum_{i=1}^{T}{w_i} = 1$。
对于 分类型的任务,学习器 $h_i$ 从类别集合 $\left\{c_1, c_2, \dotsc, c_N\right\}$ 中预测一个标签。我们将 $h_i$ 在样本 $\mathbf{x}$ 上的预测输出表示为一个 $N$ 维向量 $\left(h_i^1 \left(\mathbf{x}\right); h_i^2 \left(\mathbf{x}\right); \dotsc, h_i^N \left(\mathbf{x}\right)\right)$,其中 $h_i^j \left(\mathbf{x}\right)$ 为 $h_i$ 在类型标签 $c_j$ 上的输出。
- 绝对多数投票法 (Majority Voting)
$$ H \left(\mathbf{x}\right) = \begin{cases} c_j, & \displaystyle\sum_{i=1}^{M}{h_i^j \left(\mathbf{x}\right) > 0.5 \displaystyle\sum_{k=1}^{N}{\displaystyle\sum_{i=1}^{M}{h_i^k \left(\mathbf{x}\right)}}} \\ \text{refuse}, & \text{other wise} \end{cases} $$
即如果一个类型的标记得票数过半,则预测为该类型,否则拒绝预测。
- 相对多数投票法 (Plurality Voting)
$$ H \left(\mathbf{x}\right) = c_{\arg\max_j \sum_{i=1}^{M}{h_i^j \left(\mathbf{x}\right)}} $$
即预测为得票数最多的类型,如果同时有多个类型获得相同最高票数,则从中随机选取一个。
- 加权投票法 (Weighted Voting)
$$ H \left(\mathbf{x}\right) = c_{\arg\max_j \sum_{i=1}^{M}{w_i h_i^j \left(\mathbf{x}\right)}} $$
其中,$w_i$ 为学习器 $h_i$ 的权重,且 $w_i \geq 0, \sum_{i=1}^{M}{w_i} = 1$。
绝对多数投票提供了“拒绝预测”,这为可靠性要求较高的学习任务提供了一个很好的机制,但如果学习任务要求必须有预测结果时则只能选择相对多数投票法和加权投票法。在实际任务中,不同类型的学习器可能产生不同类型的 $h_i^j \left(\boldsymbol{x}\right)$ 值,常见的有:
- 类标记,
$h_i^j \left(\mathbf{x}\right) \in \left\{0, 1\right\}$,若$h_i$将样本$\mathbf{x}$预测为类型$c_j$则取值为 1,否则取值为 0。使用类型标记的投票称之为 “硬投票” (Hard Voting)。 - 类概率,
$h_i^j \left(\mathbf{x}\right) \in \left[0, 1\right]$,相当于对后验概率$P \left(c_j \ | \ \mathbf{x}\right)$的一个估计。使用类型概率的投票称之为 “软投票” (Soft Voting)。
Stacking 24 25 方法又称为 Stacked Generalization,是一种基于分层模型组合的集成算法。Stacking 算法的基本思想如下:
- 利用初级学习算法对原始数据集进行学习,同时生成一个新的数据集。
- 根据从初级学习算法生成的新数据集,利用次级学习算法学习并得到最终的输出。
对于初级学习器,可以是相同类型也可以是不同类型的。在新的数据集中,初级学习器的输出被用作次级学习器的输入特征,初始样本的标记仍被用作次级学习器学习样本的标记。Stacking 算法的流程如下图所示:
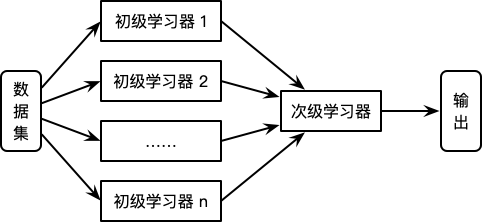
Stacking 算法过程如下:
\begin{algorithm}
\caption{Stacking 算法}
\begin{algorithmic}
\REQUIRE \\
初级学习算法 $L = \{L_1, L_2, ... L_M\}$ \\
次级学习算法 $L'$ \\
训练数据集 $T = \{(\mathbf{x}_1, y_1), (\mathbf{x}_2, y_2), ..., (\mathbf{x}_N, y_N)\}$
\ENSURE \\
Stacking 算法 $h_f\left(x\right)$
\FUNCTION{Stacking}{$L, L', T$}
\FOR{$m$ = $1$ to $M$}
\STATE $h_t \gets L_m \left(T\right)$
\ENDFOR
\STATE $T' \gets \varnothing$
\FOR{$i$ = $1$ to $N$}
\FOR{$m$ = $1$ to $M$}
\STATE $z_{im} \gets h_m(\mathbf{x}_i)$
\ENDFOR
\STATE $T' \gets T' \cup \left(\left(z_{i1}, z_{i2}, ..., z_{iM}\right), y_i\right)$
\ENDFOR
\STATE $h' \gets L' \left(T'\right)$
\STATE $h_f\left(\mathbf{x}\right) \gets h' \left(h_1\left(\mathbf{x}\right), h_2\left(\mathbf{x}\right), ..., h_M\left(\mathbf{x}\right)\right)$
\RETURN $h_f\left(\mathbf{x}\right)$
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}
次级学习器的训练集是有初级学习器产生的,如果直接利用初级学习器的训练集生成次级学习器的训练集,过拟合风险会比较大 26。因此,一般利用在训练初级学习器中未使用过的样本来生成次级学习器的训练样本。以 $k$ 折交叉检验为例:初始的训练集 $T$ 被随机划分为 $k$ 个大小相近的集合 $T_1, T_2, ..., T_k$。令 $T_j$ 和 $\overline{T}_j = T \setminus T_j$ 表示第 $j$ 折的测试集和训练集。则对于 $M$ 个初级学习算法,学习器 $h_m^{\left(j\right)}$ 是根据训练集 $\overline{T}_j$ 生成的,对于测试集 $T_j$ 中的每个样本 $\mathbf{x}_i$,得到 $z_{im} = h_m^{\left(j\right)} \left(\mathbf{x}_i\right)$。则根据 $\mathbf{x}_i$ 所产生的次级学习器的训练样本为 $\mathbf{z}_i = \left(\left(z_{i1}, z_{i2}, ..., z_{iM}\right), y_i\right)$。最终利用 $M$ 个初级学习器产生的训练集 $T' = \{\left(\mathbf{z}_i, y_i\right)\}_{i=1}^N$ 训练次级学习器。
下图展示了一些基础分类器以及 Soft Voting 和 Stacking 两种融合策略的模型在 Iris 数据集分类任务上的决策区域。数据选取 Iris 数据集中的 Sepal Length 和 Petal Length 两个特征,Stacking 中的次级学习器选择 Logistic Regression,详细实现请参见 这里。
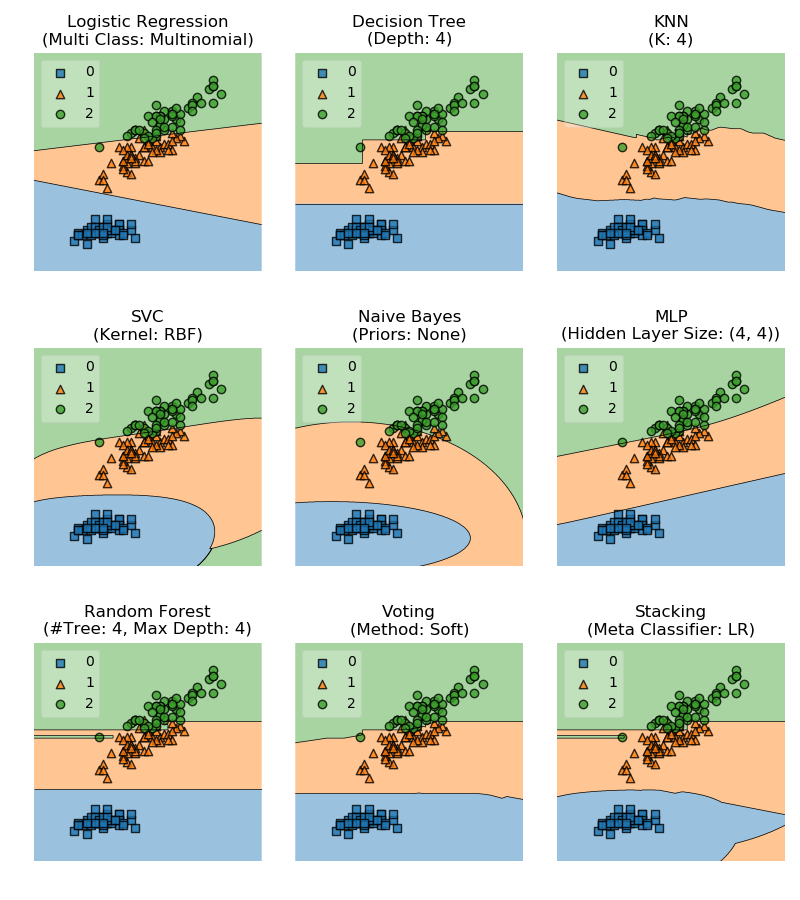
-
Dietterich, T. G. (2000, June). Ensemble methods in machine learning. In International workshop on multiple classifier systems (pp. 1-15). ↩︎
-
Dietterich, T. G. (2002). Ensemble Learning, The Handbook of Brain Theory and Neural Networks, MA Arbib. ↩︎
-
Laurent, H., & Rivest, R. L. (1976). Constructing optimal binary decision trees is NP-complete. Information processing letters, 5(1), 15-17. ↩︎
-
Blum, A., & Rivest, R. L. (1989). Training a 3-node neural network is NP-complete. In Advances in neural information processing systems (pp. 494-501). ↩︎
-
Breiman, L. (1996). Bagging predictors. Machine learning, 24(2), 123-140. ↩︎
-
Breiman, L. (2001). Random forests. Machine learning, 45(1), 5-32. ↩︎ ↩︎
-
Fernández-Delgado, M., Cernadas, E., Barro, S., & Amorim, D. (2014). Do we need hundreds of classifiers to solve real world classification problems?. The Journal of Machine Learning Research, 15(1), 3133-3181. ↩︎
-
Freund, Y., & Schapire, R. E. (1997). A decision-theoretic generalization of on-line learning and an application to boosting. Journal of computer and system sciences, 55(1), 119-139. ↩︎
-
Chen, T., & Guestrin, C. (2016). XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22Nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (pp. 785–794). ↩︎
-
Ke, G., Meng, Q., Finley, T., Wang, T., Chen, W., Ma, W., … Liu, T.-Y. (2017). LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, & R. Garnett (Eds.), Advances in Neural Information Processing Systems 30 (pp. 3146–3154). ↩︎
-
Shi, H. (2007). Best-first Decision Tree Learning (Thesis). The University of Waikato. ↩︎
-
Dorogush, A. V., Ershov, V., & Gulin, A. (2018). CatBoost: gradient boosting with categorical features support. arXiv preprint arXiv:1810.11363 ↩︎
-
Prokhorenkova, L., Gusev, G., Vorobev, A., Dorogush, A. V., & Gulin, A. (2018). CatBoost: unbiased boosting with categorical features. In S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, & R. Garnett (Eds.), Advances in Neural Information Processing Systems 31 (pp. 6637–6647). ↩︎
-
Zhang, K., Schölkopf, B., Muandet, K., & Wang, Z. (2013, February). Domain adaptation under target and conditional shift. In International Conference on Machine Learning (pp. 819-827). ↩︎
-
https://tech.yandex.com/catboost/doc/dg/concepts/python-reference_catboost_save_model-docpage ↩︎
-
https://xgboost.readthedocs.io/en/latest/gpu/index.html ↩︎ ↩︎
-
https://lightgbm.readthedocs.io/en/latest/GPU-Tutorial.html ↩︎
-
https://tech.yandex.com/catboost/doc/dg/features/training-on-gpu-docpage ↩︎ ↩︎
-
Wolpert, D. H. (1992). Stacked generalization. Neural networks, 5(2), 241-259. ↩︎
-
Breiman, L. (1996). Stacked regressions. Machine learning, 24(1), 49-64. ↩︎
-
周志华. (2016). 机器学习. 清华大学出版社. ↩︎