贝叶斯优化 (Bayesian Optimization)

范叶亮 / 2020-06-06

分类: 机器学习, 最优化 / 标签: 高斯分布, Gaussian Distribution, 正态分布, Normal Distribution, 边缘化, Marginalization, 条件化, Conditioning, 高斯过程, Gaussian Processes, 高斯过程回归, Gaussian Processes Regression, 主动学习, Active Learning, 代理模型, Surrogate Model, 贝叶斯优化, Bayesian Optimization, 采集函数, Acquisition Functions / 字数: 5045

本文内容主要参考自：

从高斯分布到高斯过程、高斯过程回归、贝叶斯优化

A Visual Exploration of Gaussian Processes

Gaussian Process Regression

Exploring Bayesian Optimization

高斯分布

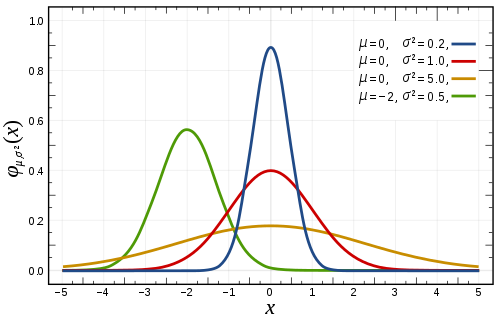
一元高斯分布

若随机变量 $X$ 服从一个均值为 $\mu$ ，方差为 $\sigma^2$ 的高斯分布，则记为：

$$ X \sim N \left(\mu, \sigma^2\right) $$

其概率密度函数为：

$$ f \left(x\right) = \dfrac{1}{\sigma \sqrt{2 \pi}} e^{- \dfrac{\left(x - \mu\right)^2}{2 \sigma^2}} $$

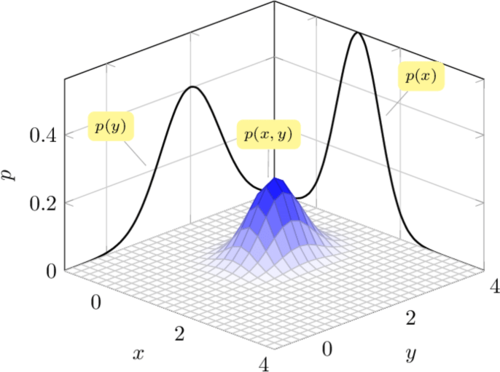
二元高斯分布

若随机变量 $X, Y$ 服从均值为 $\mu = \left(\mu_X, \mu_Y\right)^{\top}$ ，方差为 $\mu = \left(\sigma_X, \sigma_Y\right)^{\top}$ 的高斯分布，则记为：

$$ \left(X, Y\right) \sim \mathcal{N} \left(\mu, \sigma\right) $$

其概率密度函数为：

$$ f(x, y)=\frac{1}{2 \pi \sigma_{X} \sigma_{Y} \sqrt{1-\rho^{2}}} e^{-\dfrac{1}{2\left(1-\rho^{2}\right)}\left[\dfrac{\left(x-\mu_{X}\right)^{2}}{\sigma_{X}^{2}}+\dfrac{\left(y-\mu_{Y}\right)^{2}}{\sigma_{Y}^{2}}-\dfrac{2 \rho\left(x-\mu_{X}\right)\left(y-\mu_{X}\right)}{\sigma_{X} \sigma_{Y}}\right]} $$

其中， $\rho$ 是 $X$ 和 $Y$ 之间的相关系数， $\sigma_X > 0$ 且 $\sigma_Y > 0$ 。

图片来源：Bayesian tracking of multiple point targets using expectation maximization

多元高斯分布

若 $K$ 维随机向量 $X = \left[X_1, \cdots, X_K\right]^{\top}$ 服从多元高斯分布，则必须满足如下三个等价条件：

任何线性组合 $Y = a_1 X_1 + \cdots a_K X_K$ 均服从高斯分布。
存在随机向量 $Z = \left[Z_1, \cdots, Z_L\right]^{\top}$ （每个元素服从独立标准高斯分布），向量 $\mu = \left[\mu_1, \cdots, \mu_K\right]^{\top}$ 以及 $K \times L$ 的矩阵 $A$ ，满足 $X = A Z + \mu$ 。
存在 $\mu$ 和一个对称半正定矩阵 $\Sigma$ 满足 $X$ 的特征函数 $\phi_X \left(u; \mu, \Sigma\right) = \exp \left(i \mu^{\top} u - \dfrac{1}{2} u^{\top} \Sigma u\right)$

如果 $\Sigma$ 是非奇异的，则概率密度函数为：

$$ f \left(x_1, \cdots, x_k\right) = \dfrac{1}{\sqrt{\left(2 \pi\right)^k \lvert\Sigma\rvert}} e^{- \dfrac{1}{2} \left(x - \mu\right)^{\top} \Sigma^{-1} \left(x - \mu\right)} $$

其中 $\lvert\Sigma\rvert$ 表示协方差矩阵的行列式。

边缘化和条件化

高斯分布具有一个优秀的代数性质，即在边缘化和条件化下是闭合的，也就是说从这些操作中获取的结果分布也是高斯的。**边缘化（Marginalization）和条件化（Conditioning）**都作用于原始分布的子集上：

$$ P_{X, Y}=\left[\begin{array}{l} X \\ Y \end{array}\right] \sim \mathcal{N}(\mu, \Sigma)=\mathcal{N}\left(\left[\begin{array}{l} \mu_{X} \\ \mu_{Y} \end{array}\right],\left[\begin{array}{l} \Sigma_{X X} \Sigma_{X Y} \\ \Sigma_{Y X} \Sigma_{Y Y} \end{array}\right]\right) $$

其中， $X$ 和 $Y$ 表示原始随机变量的子集。

对于随机向量 $X$ 和 $Y$ 的高斯概率分布 $P \left(X, Y\right)$ ，其边缘概率分布为：

$$ \begin{array}{l} X \sim \mathcal{N}\left(\mu_{X}, \Sigma_{X X}\right) \\ Y \sim \mathcal{N}\left(\mu_{Y}, \Sigma_{Y Y}\right) \end{array} $$

$X$ 和 $Y$ 两个子集各自只依赖于 $\mu$ 和 $\Sigma$ 中它们对应的值。因此从高斯分布中边缘化一个随机变量仅需从 $\mu$ 和 $\Sigma$ 中舍弃相应的变量即可：

$$ p_{X}(x)=\int_{y} p_{X, Y}(x, y) d y=\int_{y} p_{X | Y}(x | y) p_{Y}(y) d y $$

条件化可以用于得到一个变量在另一个变量条件下的概率分布：

$$ \begin{array}{l} X | Y \sim \mathcal{N}\left(\mu_{X}+\Sigma_{X Y} \Sigma_{Y Y}^{-1}\left(Y-\mu_{Y}\right), \Sigma_{X X}-\Sigma_{X Y} \Sigma_{Y Y}^{-1} \Sigma_{Y X}\right) \\ Y | X \sim \mathcal{N}\left(\mu_{Y}+\Sigma_{Y X} \Sigma_{X X}^{-1}\left(X-\mu_{X}\right), \Sigma_{Y Y}-\Sigma_{Y X} \Sigma_{X X}^{-1} \Sigma_{X Y}\right) \end{array} $$

需要注意新的均值仅依赖于作为条件的变量，协方差矩阵和这个变量无关。

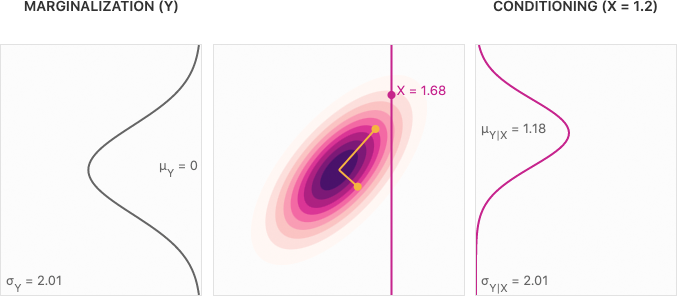
边缘化可以理解为在高斯分布的一个维度上的累加，条件化可以理解为在多元分布上切一刀从而获得一个维数更少的高斯分布，如下图所示：

高斯过程

**高斯过程（Gaussian Process）**是观测值出现在一个连续域（例如时间或空间）的随机过程。在高斯过程中，连续输入空间中每个点都是与一个正态分布的随机变量相关联。此外，这些随机变量的每个有限集合都有一个多元正态分布，换句话说它们的任意有限线性组合是一个正态分布。高斯过程的分布是所有那些（无限多个）随机变量的联合分布，正因如此，它是连续域（例如时间或空间）上函数的分布。

简单而言，高斯过程即为一系列随机变量，这些随机变量的任意有限集合均为一个多元高斯分布。从一元高斯分布到多元高斯分布相当于增加了空间维度，从高斯分布到高斯过程相当于引入了时间维度。一个高斯过程可以被均值函数 $m \left(x\right)$ 和协方差函数 $K \left(x, x'\right)$ 共同唯一确定：

$$ \begin{aligned} m(x) &=\mathbb{E}[f(x)] \\ K\left(x, x'\right) &=\mathbb{E}\left[(f(x)-m(x))\left(f\left(x^{\prime}\right)-m\left(x^{\prime}\right)\right)\right] \end{aligned} $$

则高斯过程可以表示为：

$$ f \left(x\right) \sim \mathcal{GP} \left(m \left(x\right), K \left(x, x'\right)\right) $$

均值函数决定了样本出现的整体位置，如果为零则表示以 $y = 0$ 为基准线。协方差函数描述了不同点之间的关系，从而可以利用输入的训练数据预测未知点的值。常用的协方差函数有：

常数： $K_c \left(x, x'\right) = C$
线性： $K_L \left(x, x'\right) = x^{\top} x'$
高斯噪声： $K_{GN} \left(x, x'\right) = \sigma^2 \delta_{x, x'}$
指数平方： $K_{\mathrm{SE}}\left(x, x^{\prime}\right)=\exp \left(-\dfrac{|d|^{2}}{2 \ell^{2}}\right)$
Ornstein-Uhlenbeck： $K_{\mathrm{OU}}\left(x, x^{\prime}\right)=\exp \left(-\dfrac{|d|}{\ell}\right)$
Matérn： $K_{\text {Matern }}\left(x, x^{\prime}\right)=\dfrac{2^{1-\nu}}{\Gamma(\nu)}\left(\dfrac{\sqrt{2 \nu}|d|}{\ell}\right)^{\nu} K_{\nu}\left(\dfrac{\sqrt{2 \nu}|d|}{\ell}\right)$
周期： $K_{\mathrm{P}}\left(x, x^{\prime}\right)=\exp \left(-\dfrac{2 \sin ^{2}\left(\dfrac{d}{2}\right)}{\ell^{2}}\right)$
有理平方： $K_{\mathrm{RQ}}\left(x, x^{\prime}\right)=\left(1+|d|^{2}\right)^{-\alpha}, \quad \alpha \geq 0$

高斯过程回归

回归任务的目标是给定一个输入变量 $x \in \mathbb{R}^D$ 预测一个或多个连续目标变量 $y$ 的值。更确切的说，给定一个包含 $N$ 个观测值的训练集 $\mathbf{X} = \left\{x_n\right\}^N_1$ 和对应的目标值 $\mathbf{Y} = \left\{y_n\right\}^N_1$ ，回归的目标是对于一个新的 $x$ 预测对应的 $y$ 。目标值和观测值之间通过一个映射进行关联：

$$ f: X \to Y $$

在贝叶斯模型中，我们通过观测数据 $\mathcal{D} = \left\{\left(\mathbf{x}_n, \mathbf{y}_n\right)\right\}^N_{n=1}$ 更新先验分布 $P \left(\mathbf{\Theta}\right)$ 。通过贝叶斯公式我们可以利用先验概率 $P \left(\mathbf{\Theta}\right)$ 和似然函数 $P \left(\mathcal{D} | \mathbf{\Theta}\right)$ 推导出后验概率：

$$ p\left(\mathbf{\Theta} | \mathcal{D}\right)=\frac{p\left(\mathcal{D} | \mathbf{\Theta}\right) p\left(\mathbf{\Theta}\right)}{p\left(\mathcal{D}\right)} $$

其中 $p\left(\mathcal{D}\right)$ 为边际似然。在贝叶斯回归中我们不仅希望获得未知输入对应的预测值 $\mathbf{y}_*$ ，还希望知道预测的不确定性。因此我们需要利用联合分布和边缘化模型参数 $\mathbf{\Theta}$ 来构造预测分布：

$$ p\left(\mathbf{y}_{*} | \mathbf{x}_{*}, \mathcal{D}\right)=\int p\left(\mathbf{y}_{*}, \mathbf{\Theta} | \mathbf{x}_{*}, \mathcal{D}\right) \mathrm{d} \Theta=\int p\left(\mathbf{y}_{*} | \mathbf{x}_{*}, \mathbf{\Theta}, \mathcal{D}\right) p(\mathbf{\Theta} | \mathcal{D}) \mathrm{d} \mathbf{\Theta} $$

通常情况下，由于积分形式 $p \left(\Theta | \mathcal{D}\right)$ 不具有解析可解性（Analytically Tractable）：

$$ p\left(\mathcal{D}\right)=\int p\left(\mathcal{D} | \mathbf{\Theta}\right) p\left(\mathbf{\Theta}\right) d \Theta $$

但在高斯似然和高斯过程先验的前提下，后验采用函数的高斯过程的形式，同时是解析可解的。

对于高斯过程回归，我们构建一个贝叶斯模型，首先定义函数输出的先验为一个高斯过程：

$$ p \left(f | \mathbf{X}, \theta\right) = \mathcal{N} \left(\mathbf{0}, K \left(\mathbf{X}, \mathbf{X}\right)\right) $$

其中 $K \left(\cdot, \cdot\right)$ 为协方差函数， $\theta$ 为过程的超参数。假设数据已经变换为零均值，因此我们不需要在先验中设置均值函数，则令似然形式如下：

$$ p \left(\mathbf{Y} | f\right) \sim \mathcal{N} \left(f, \sigma^2_n \mathbf{I}\right) $$

假设观测值为独立同分布的高斯噪音的累加，则整个模型的联合分布为：

$$ p \left(\mathbf{Y} , f | \mathbf{X}, \theta\right) = p \left(\mathbf{Y} | f\right) p \left(f | \mathbf{X}, \theta\right) $$

虽然我们并不关心变量 $f$ ，但由于我们需要对不确定性进行建模，我们仍需考虑 $\mathbf{Y}$ 和 $f$ 以及 $f$ 和 $\mathbf{X}$ 之间的关系。高斯过程作为一个非参数模型，其先验分布构建于映射 $f$ 之上， $f$ 仅依赖于核函数的超参数 $\theta$ ，且这些超参数可以通过数据进行估计。我们可以将超参数作为先验，即：

$$ p \left(\mathbf{Y} , f | \mathbf{X}, \theta\right) = p \left(\mathbf{Y} | f\right) p \left(f | \mathbf{X}, \theta\right) p \left(\theta\right) $$

然后进行贝叶斯推断和模型选择，但是通常情况下这是不可解的。David MacKay 引入了一个利用最优化边际似然来估计贝叶斯平均的框架，即计算如下积分：

$$ p \left(\mathbf{Y} | \mathbf{X}, \theta\right) = \int p \left(\mathbf{Y} | f\right) p \left(f | \mathbf{X}, \theta\right) df $$

其中，高斯似然 $p \left(\mathbf{Y} | f\right)$ 表示模型拟合数据的程度， $p \left(f | \mathbf{X}, \theta\right)$ 为高斯过程先验。经过边缘化后， $\mathbf{Y}$ 不在依赖于 $f$ 而仅依赖于 $\theta$ 。

假设采用零均值函数，对于一个高斯过程先验，我们仅需指定一个协方差函数。以指数平方协方差函数为例，选择一系列测试输入点 $X_*$ ，利用协方差矩阵和测试输入点可以生成一个高斯向量：

$$ \mathbf{f}_* \sim \mathcal{N} \left(\mathbf{0}, K \left(X_*, X_*\right)\right) $$

从高斯先验中进行采样，我们首先需要利用标准正态来表示多元正态：

$$ \mathbf{f}_* \sim \mu + \mathbf{B} \mathcal{N} \left(0, \mathbf{I}\right) $$

其中， $\mathbf{BB}^{\top} = K \left(X_*, X_*\right)$ ， $\mathbf{B}$ 本质上是协方差矩阵的平方根，可以通过 Cholesky 分解获得。

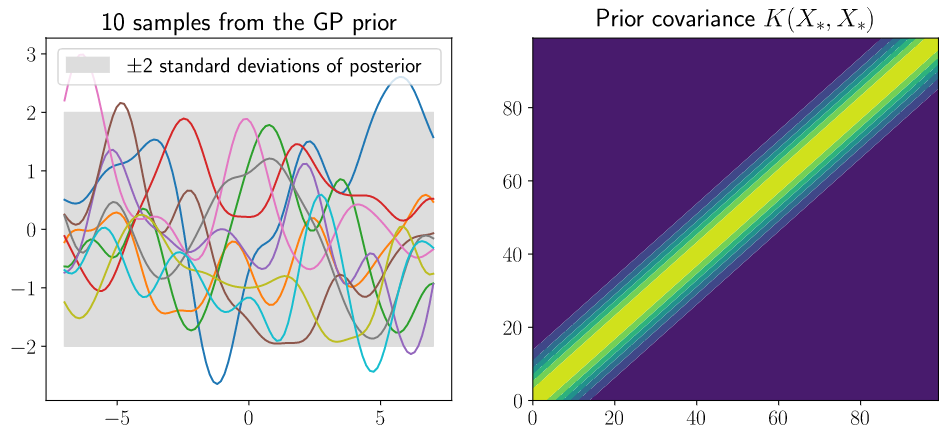
上图（左）为从高斯先验中采样的 10 个序列，上图（右）为先验的协方差。如果输入点 $x_n$ 和 $x_m$ 接近，则对应的 $f \left(x_n\right)$ 和 $f \left(x_m\right)$ 相比于不接近的点是强相关的。

我们关注的并不是这些随机的函数，而是如何将训练数据中的信息同先验进行合并。假设观测数据为 $\left\{\left(\mathbf{x}_{i}, f_{i}\right) | i=1, \ldots, n\right\}$ ，则训练目标 $\mathbf{f}$ 和测试目标 $\mathbf{f}_*$ 之间的联合分布为：

$$ \left[\begin{array}{l} \mathbf{f} \\ \mathbf{f}_{*} \end{array}\right] \sim \mathcal{N}\left(\mathbf{0},\left[\begin{array}{ll} K(X, X) & K\left(X, X_{*}\right) \\ K\left(X_{*}, X\right) & K\left(X_{*}, X_{*}\right) \end{array}\right]\right) $$

根据观测值对联合高斯先验分布进行条件化处理可以得到高斯过程回归的关键预测方程：

$$ \mathbf{f}_{*} | X, X_{*}, \mathbf{f} \sim \mathcal{N}\left(\overline{\mathbf{f}}_{*}, \operatorname{cov}\left(\mathbf{f}_{*}\right)\right) $$

其中

$$ \begin{aligned} \overline{\mathbf{f}}_{*} & \triangleq \mathbb{E}\left[\mathbf{f}_{*} | X, X_{*}, \mathbf{f}\right]=K\left(X_{*}, X\right) K(X, X)^{-1} \mathbf{f} \\ \operatorname{cov}\left(\mathbf{f}_{*}\right) &=K\left(X_{*}, X_{*}\right)-K\left(X_{*}, X\right) K(X, X)^{-1} K\left(X, X_{*}\right) \end{aligned} $$

函数值可以通过对联合后验分布采样获得。

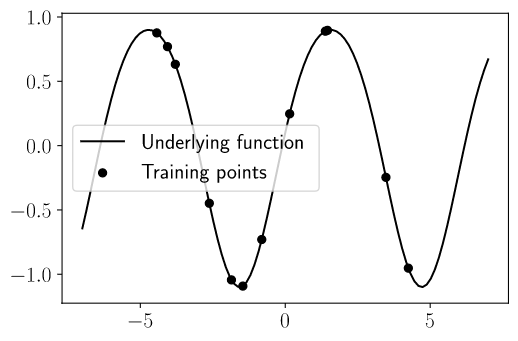
我们以三角函数作为给定的函数，并随机采样一些训练数据 $\left\{\left(\mathbf{x}_{i}, f_{i}\right) | i=1, \ldots, n\right\}$ ，如下图所示：

我们希望将训练数据和高斯过程先验进行合并得到联合后验分布，我们可以通过在观测值上条件化联合高斯先验分布，预测的均值和协方差为：

$$ \begin{aligned} \overline{\mathbf{f}}_{*} &=K\left(X_{*}, X\right) K(X, X)^{-1} \mathbf{f} \\ \operatorname{cov}\left(\mathbf{f}_{*}\right) &=K\left(X_{*}, X_{*}\right)-K\left(X_{*}, X\right) K(X, X)^{-1} K\left(X, X_{*}\right) \end{aligned} $$

Rasmussen 和 Williams 给出了一个实现高斯过程回归的实用方法：

\begin{algorithm}
\caption{高斯过程回归算法}
\begin{algorithmic}
\REQUIRE \\
    输入 $\mathbf{X}$ \\
    目标 $\mathbf{y}$ \\
    协方差函数 $k$ \\
    噪音水平 $\sigma^2_n$ \\
    测试输入 $\mathbf{x}_*$
\ENSURE \\
    均值 $\bar{f}_*$ \\
    方差 $\mathbb{V}\left[f_{*}\right]$
\FUNCTION{GaussianProcessRegression}{$\mathbf{X}, \mathbf{y}, k, \sigma^2_n, \mathbf{x}_*$}
\STATE $L \gets \text{cholesky} \left(K + \sigma^2_n I\right)$
\STATE $\alpha \gets L^{\top} \setminus \left(L \setminus \mathbf{y}\right)$
\STATE $\bar{f}_* \gets \mathbf{k}^{\top}_* \alpha$
\STATE $\mathbf{v} \gets L \setminus \mathbf{k}_*$
\STATE $\mathbb{V}\left[f_{*}\right] \gets k \left(\mathbf{x}_*, \mathbf{x}_*\right) - \mathbf{v}^{\top} \mathbf{v}$
\RETURN $\bar{f}_*, \mathbb{V}\left[f_{*}\right]$
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}

高斯过程后验和采样的序列如下图所示：

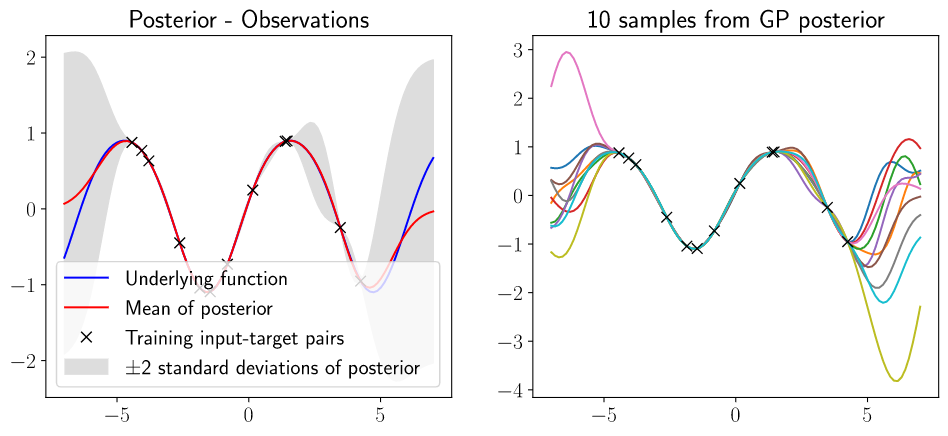
先验的协方差矩阵和后验的协方差矩阵可视化如下图所示：

本小结代码请参见这里。

贝叶斯优化

主动学习

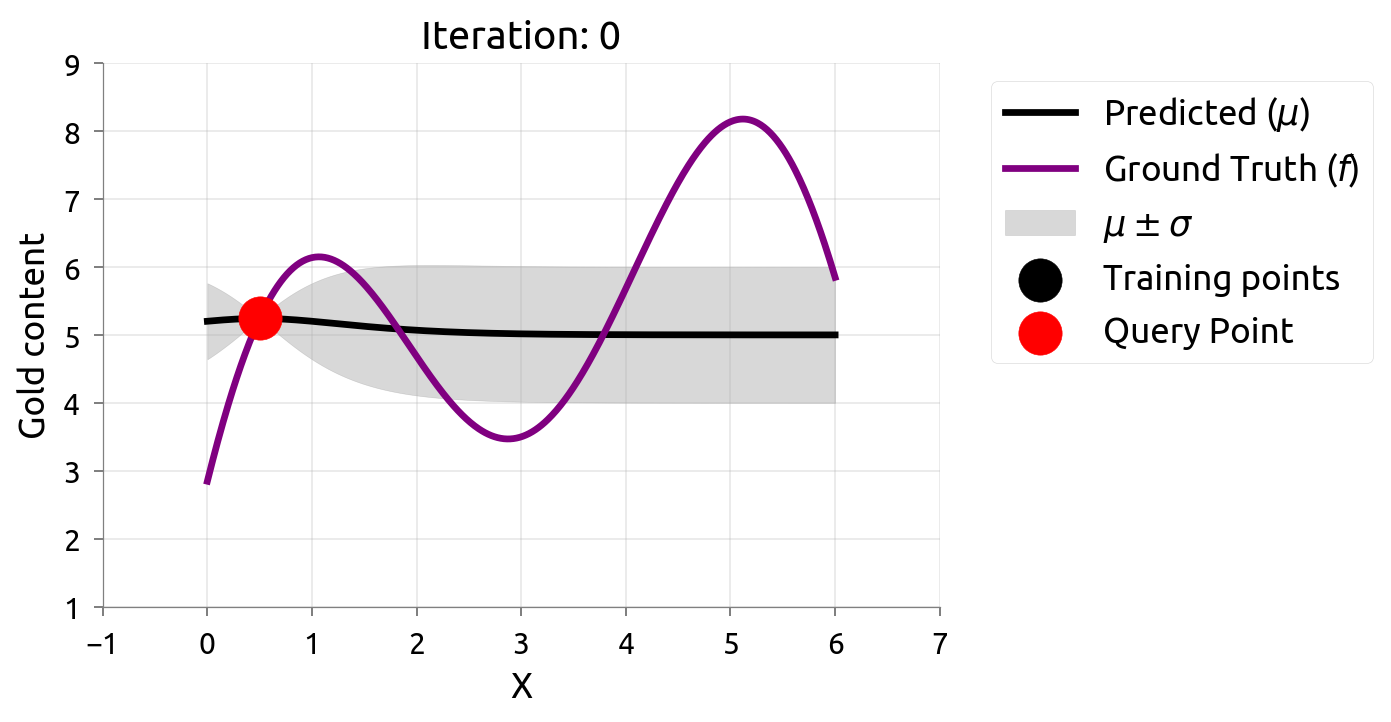
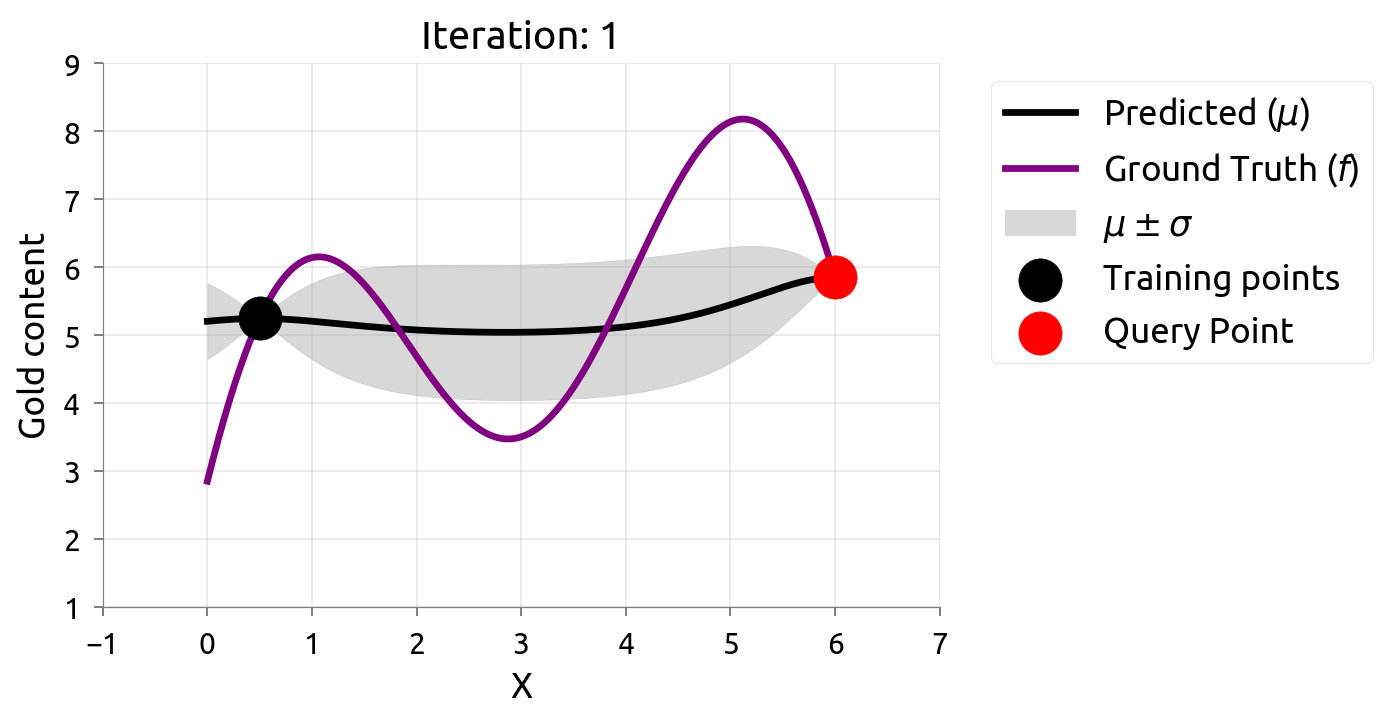
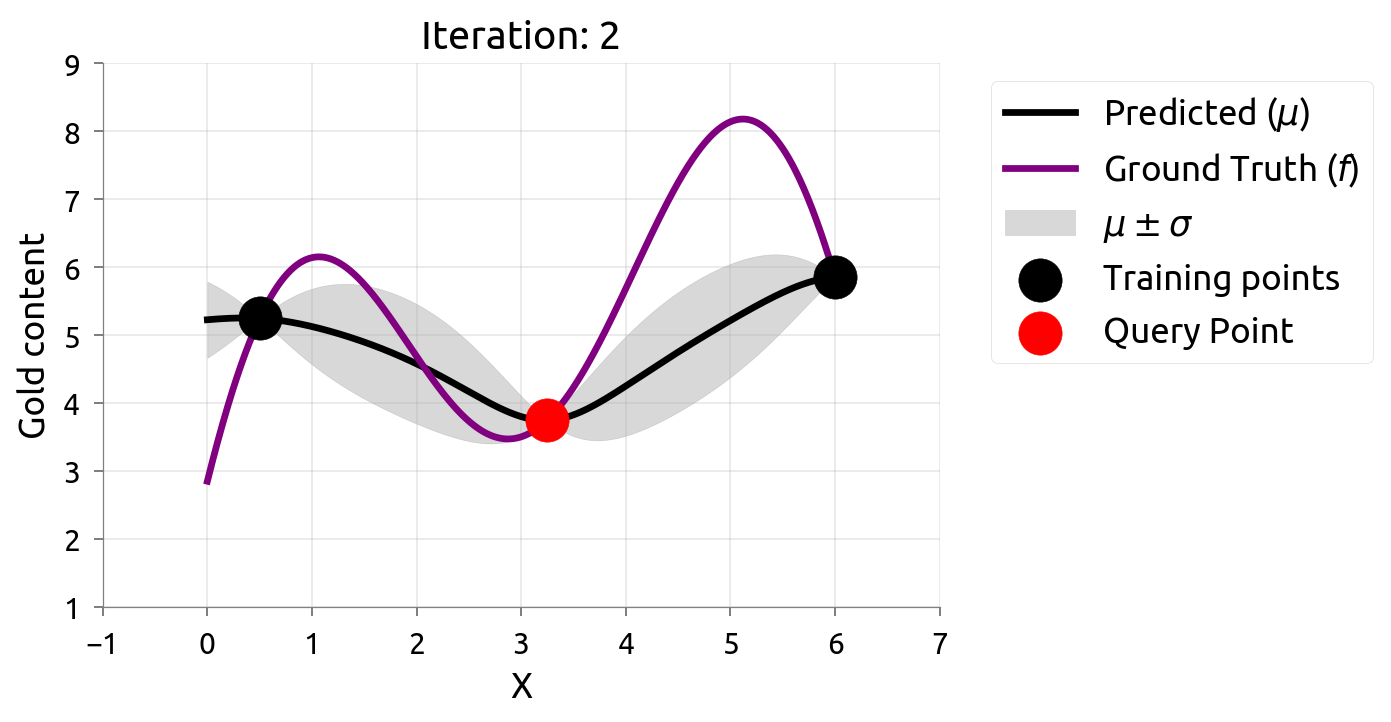
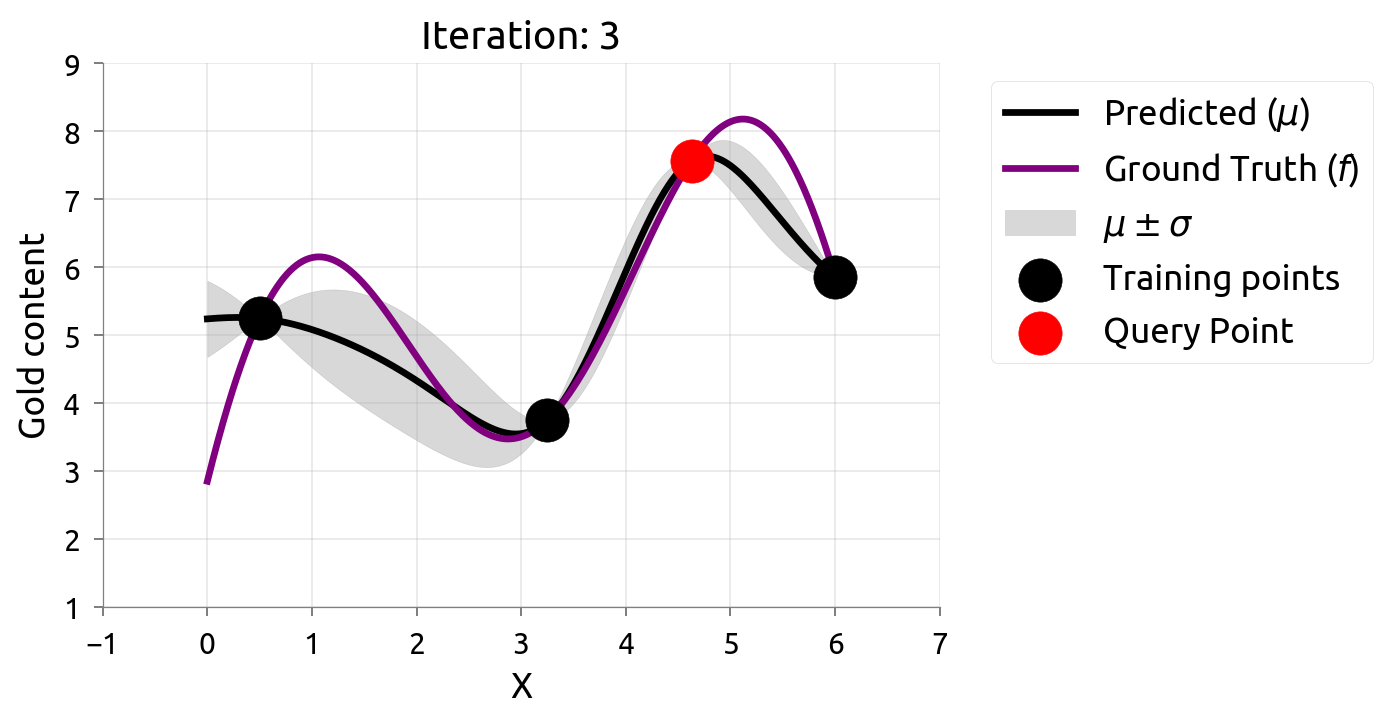
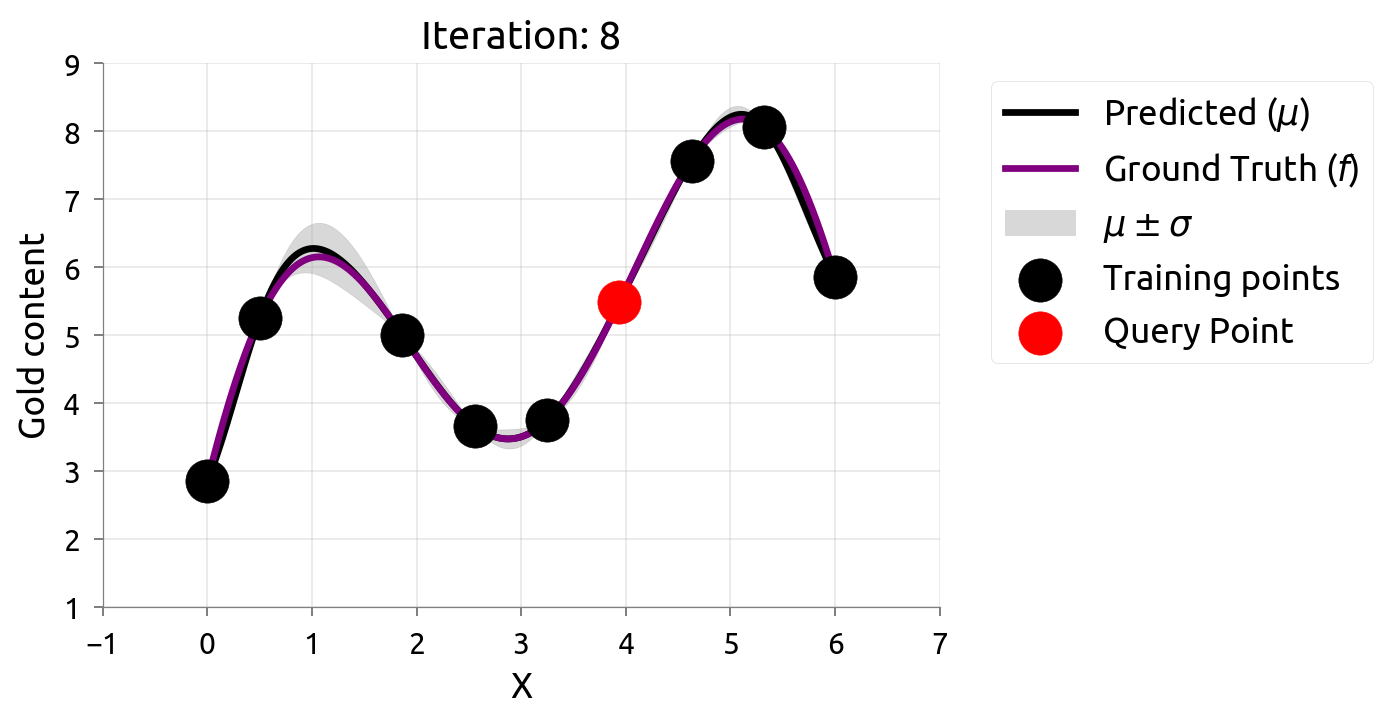
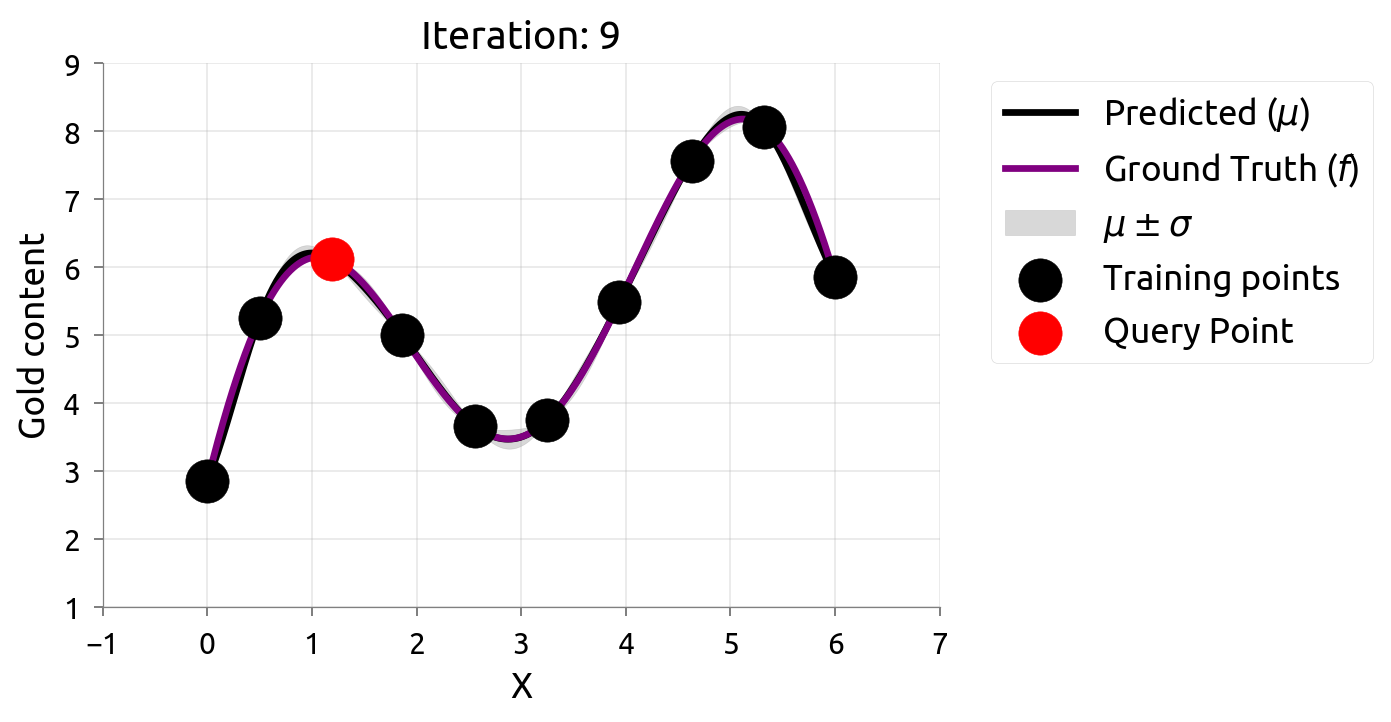
在很多机器学习问题中，数据标注往往需要耗费很大成本。**主动学习（Active Learning）**在最大化模型准确率时最小化标注成本，例如对不确定性最高的数据进行标注。由于我们仅知道少量数据点，因此我们需要一个代理模型（Surrogate Model）来建模真正的模型。高斯过程因其灵活性和具有估计不确定性估计的特性不失为一个常用的代理模型。

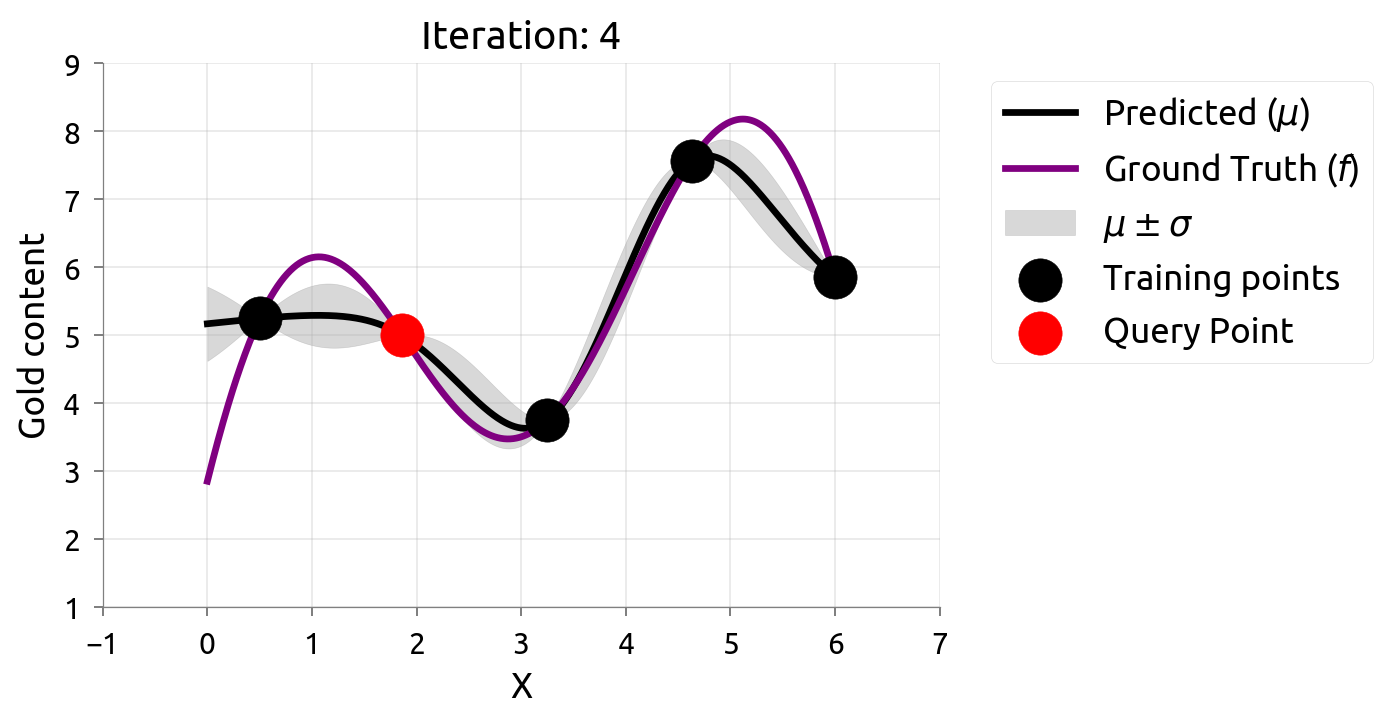
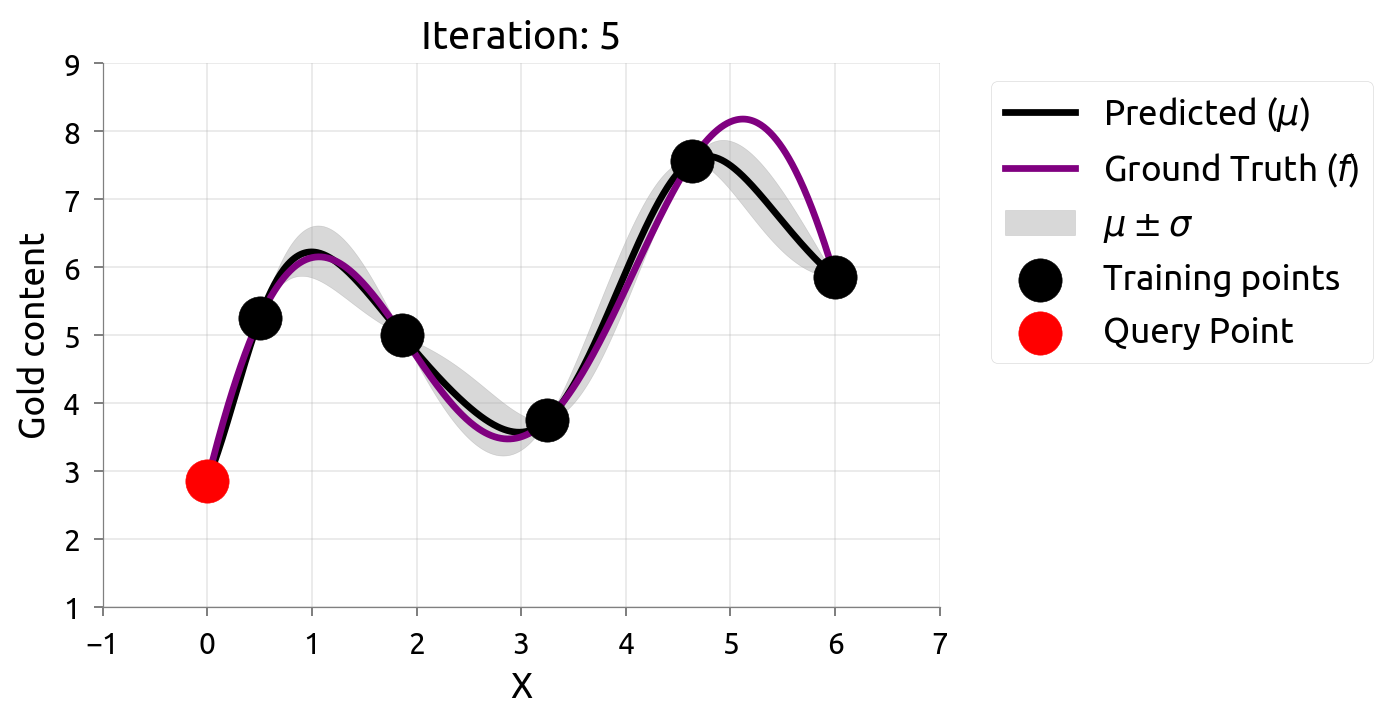
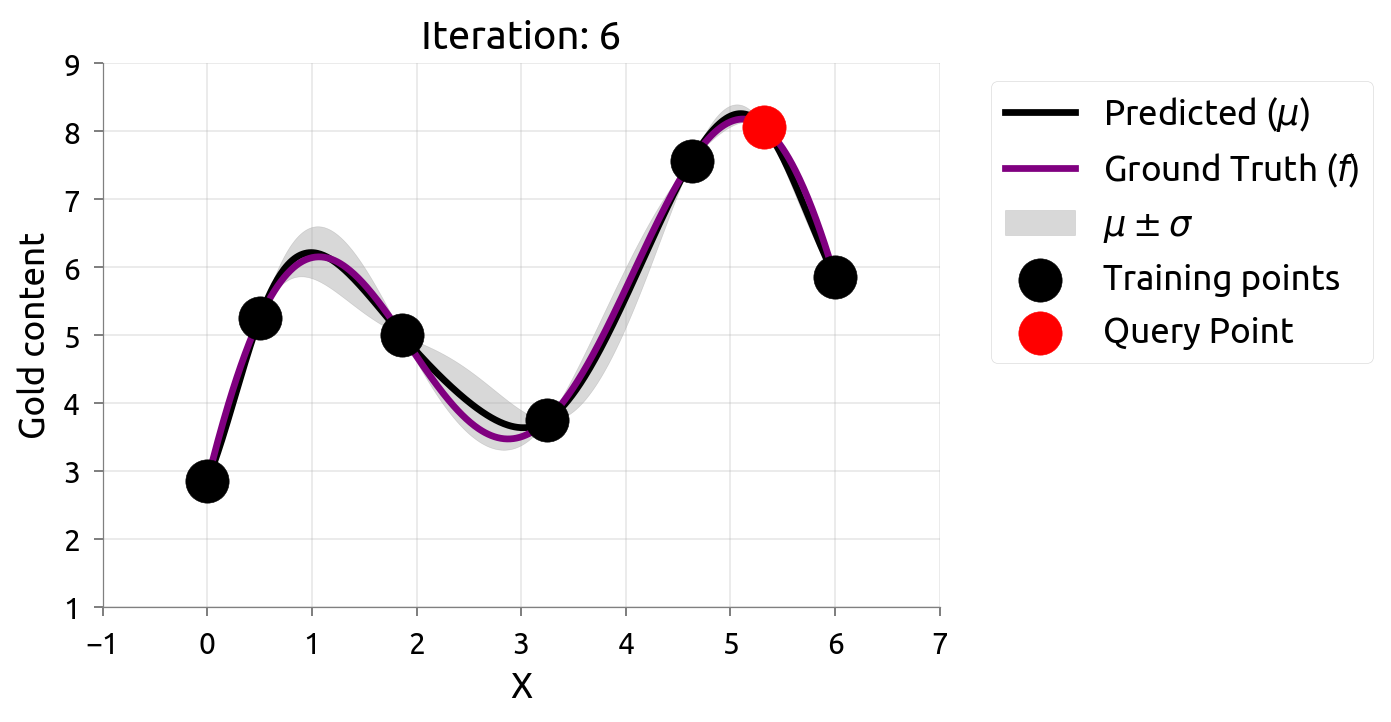
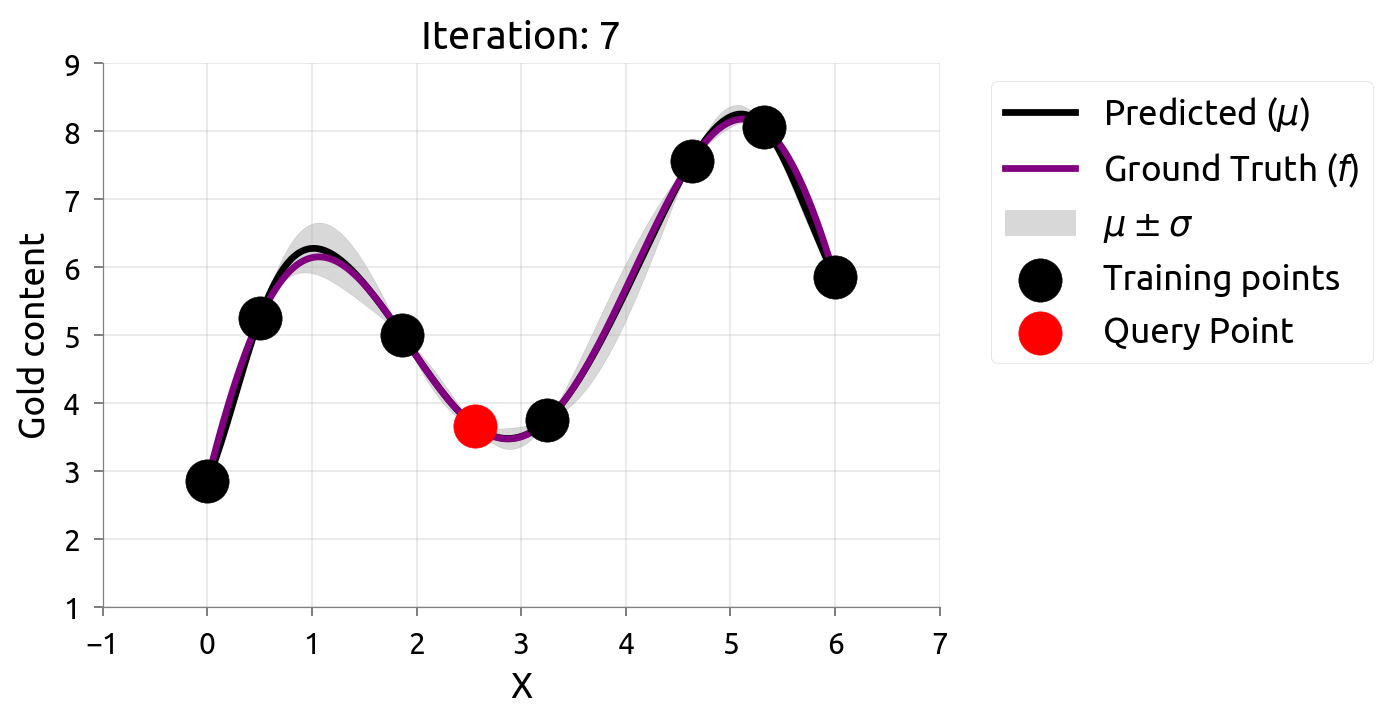
在估计 $f \left(x\right)$ 的过程中，我们希望最小化评估的次数，因此我们可以通过主动学习来“智能”地选择下一个评估的数据点。通过不断的选择具有最高不确定性的数据点来获得 $f \left(x\right)$ 更准确的估计，直至收敛或达到停止条件。下图展示了利用主动学习估计真实数据分布的过程：

/images/cn/2020-06-06-bayesian-optimization/ active-gp- png 300

贝叶斯优化问题

贝叶斯优化的核心问题是：基于现有的已知情况，如果选择下一步评估的数据点？在主动学习中我们选择不确定性最大的点，但在贝叶斯优化中我们需要在探索不确定性区域（探索）和关注已知具有较优目标值的区域之间进行权衡（开发）。这种评价的依据称之为采集函数（Acquisition Functions），采集函数通过当前模型启发式的评估是否选择一个数据点。

贝叶斯优化的目标是找到一个函数 $f: \mathbb{R}^d \mapsto \mathbb{R}$ 最大值（或最小值）对应的位置 $x \in \mathbb{R}^d$ 。为了解决这个问题，我们遵循如下算法：

选择一个代理模型用于建模真实函数 $f$ 和定义其先验。
给定观测集合，利用贝叶斯公式获取后验。
利用采集函数 $\alpha \left(x\right)$ 确性下一个采样点 $x_t = \arg\max_x \alpha \left(x\right)$ 。
将采样的点加入观测集合，重复步骤 2 直至收敛或达到停止条件。

采集函数

Probability of Improvement (PI)

Probability of Improvement (PI) 采集函数会选择具有最大可能性提高当前最大的 $f \left(x^{+}\right)$ 值的点作为下一个查询点，即：

$$ x_{t+1} = \arg\max \left(\alpha_{PI} \left(x\right)\right) = \arg\max \left(P \left(f \left(x\right)\right) \geq \left(f \left(x^{+}\right) + \epsilon\right)\right) $$

其中， $P \left(\cdot\right)$ 表示概率， $\epsilon$ 为一个较小的正数， $x^{+} = \arg\max_{x_i \in x_{1:t}} f \left(x_i\right)$ ， $x_i$ 为第 $i$ 步查询点的位置。如果采用高斯过程作为代理模型，上式则转变为：

$$ x_{t+1} = \arg\max_x \Phi \left(\dfrac{\mu_t \left(x\right) - f \left(x^{+}\right) - \epsilon}{\sigma_t \left(x\right)}\right) $$

其中， $\Phi \left(\cdot\right)$ 表示标准正态分布累积分布函数。PI 利用 $\epsilon$ 来权衡探索和开发，增加 $\epsilon$ 的值会更加倾向进行探索。

Expected Improvement (EI)

PI 仅关注了有多大的可能性能够提高，而没有关注能够提高多少。Expected Improvement (EI) 则会选择具有最大期望提高的点作为下一个查询点，即：

$$ x_{t+1} = \arg\min_x \mathbb{E} \left(\left\|h_{t+1} \left(x\right) - f \left(x^*\right)\right\| | \mathcal{D}_t\right) $$

其中， $f$ 为真实函数， $h_{t+1}$ 为代理模型在 $t+1$ 步的后验均值， $\mathcal{D}_t = \left\{\left(x_i, f\left(x_i\right)\right)\right\}, \forall x \in x_{1:t}$ 为训练数据， $x^*$ 为 $f$ 取得最大值的真实位置。

上式中我们希望选择能够最小化与最大目标值之间距离的点，由于我们并不知道真实函数 $f$ ，Mockus ¹ 提出了一种解决办法：

$$ x_{t+1} = \arg\max_x \mathbb{E} \left(\max \left\{0, h_{t+1} \left(x\right) - f \left(x^{+}\right)\right\} | \mathcal{D}_t\right) $$

其中， $f \left(x^{+}\right)$ 为到目前为止遇见的最大函数值，如果采用高斯过程作为代理模型，上式则转变为：

$$ \begin{aligned} EI(x) &= \left\{\begin{array}{ll} \left(\mu_{t}(x)-f\left(x^{+}\right)-\epsilon\right) \Phi(Z)+\sigma_{t}(x) \phi(Z), & \text { if } \sigma_{t}(x)>0 \\ 0 & \text { if } \sigma_{t}(x)=0 \end{array}\right. \\ Z &= \frac{\mu_{t}(x)-f\left(x^{+}\right)-\epsilon}{\sigma_{t}(x)} \end{aligned} $$

其中 $\Phi \left(\cdot\right)$ 表示标准正态分布累积分布函数， $\phi \left(\cdot\right)$ 表示标准正态分布概率密度函数。类似 PI，EI 也可以利用 $\epsilon$ 来权衡探索和开发，增加 $\epsilon$ 的值会更加倾向进行探索。

对比和其他采集函数

上图展示了在仅包含一个训练观测数据 $\left(0.5, f \left(0.5\right)\right)$ 情况下不同点的采集函数值。可以看出 $\alpha_{EI}$ 和 $\alpha_{PI}$ 的最大值分别为 0.3 和 0.47。选择一个具有较小的 $\alpha_{PI}$ 和一个较大的 $\alpha_{EI}$ 的点可以理解为一个高的风险和高的回报。因此，当多个点具有相同的 $\alpha_{EI}$ 时，我们应该优先选择具有较小风险（高 $\alpha_{PI}$ ）的点，类似的，当多个点具有相同的 $\alpha_{PI}$ 时，我们应该优先选择具有较大回报（高 $\alpha_{EI}$ ）的点。

其他采集函数还有 Thompson Sampling ²，Upper Confidence Bound (UCB)，Gaussian Process Upper Confidence Bound (GP-UCB) ³，Entropy Search ⁴，Predictive Entropy Search ⁵ 等，细节请参见原始论文或 A Tutorial on Bayesian Optimization ⁶。

开放资源

Mockus, J. B., & Mockus, L. J. (1991). Bayesian approach to global optimization and application to multiobjective and constrained problems. Journal of Optimization Theory and Applications, 70(1), 157-172. ↩︎
Thompson, W. R. (1933). On the likelihood that one unknown probability exceeds another in view of the evidence of two samples. Biometrika, 25(3/4), 285-294. ↩︎
Auer, P. (2002). Using confidence bounds for exploitation-exploration trade-offs. Journal of Machine Learning Research, 3(Nov), 397-422. ↩︎
Hennig, P., & Schuler, C. J. (2012). Entropy search for information-efficient global optimization. Journal of Machine Learning Research, 13(Jun), 1809-1837. ↩︎
Hernández-Lobato, J. M., Hoffman, M. W., & Ghahramani, Z. (2014). Predictive entropy search for efficient global optimization of black-box functions. In Advances in neural information processing systems (pp. 918-926). ↩︎
Frazier, P. I. (2018). A tutorial on bayesian optimization. arXiv preprint arXiv:1807.02811. ↩︎

bayesian-optimization