深度学习优化算法 (Optimization Methods for Deeplearning)
范叶亮 / 2018-02-24
分类: 机器学习, 深度学习 / 标签: 梯度下降, SGD, Momentum, NAG, AdaGrad, Adadelta, RMSProp, Adam, Adamax, Nadam, AMSGrad / 字数: 4043
在构建神经网络模型的时候,除了网络结构设计以外,选取合适的优化算法也对网络起着至关重要的作用,本文将对神经网络中常用的优化算法进行简单的介绍和对比,本文部分参考了 Ruder 的关于梯度下降优化算法一文 1。首先,我们对下文中使用的符号进行同意说明:网络中的参数同一表示为 $\theta$,网络的假设函数为 $h_{\boldsymbol{\theta}}\left(\boldsymbol{x}\right)$,网络的损失函数为 $J\left(\boldsymbol{\theta}\right)$,学习率为 $\alpha$,假设训练数据中共包含 $m$ 个样本,网络参数个数为 $n$。
梯度下降
在梯度下降算法中,常用的主要包含 3 种不同的形式,分别是批量梯度下降 (Batch Gradient Descent, BGD),随机梯度下降 (Stochastic Gradient Descent, SGD) 和小批量梯度下降 (Mini-Batch Gradient Descent, MBGD)。一般情况下,我们在谈论梯度下降时,更多的是指小批量梯度下降。
BGD
BGD 为梯度下降算法中最基础的一个算法,其损失函数定义如下:
$$ J \left(\boldsymbol{\theta}\right) = \dfrac{1}{2m} \sum_{i=1}^{m}{\left(h_{\boldsymbol{\theta}}\left(x^{\left(i\right)}\right) - y^{\left(i\right)}\right)} $$
针对任意参数 $\theta_j$ 我们可以求得其梯度为:
$$ \nabla_{\theta_j} = \dfrac{\partial J\left(\boldsymbol{\theta}\right)}{\partial \theta_j} = - \dfrac{1}{m} \sum_{i=1}^{m}{\left(y^{\left(i\right)} - h_{\boldsymbol{\theta}} \left(x^{\left(i\right)}\right)\right) x_j^{\left(i\right)}} $$
之后,对于任意参数 $\theta_j$ 我们按照其负梯度方向进行更新:
$$ \theta_j = \theta_j + \alpha \left[\dfrac{1}{m} \sum_{i=1}^{m}{\left(y^{\left(i\right)} - h_{\boldsymbol{\theta}} \left(x^{\left(i\right)}\right)\right) x_j^{\left(i\right)}}\right] $$
整个算法流程可以表示如下:
\begin{algorithm}
\caption{BGD 算法}
\begin{algorithmic}
\FOR{$epoch = 1, 2, ...$}
\FOR{$j = 1, 2, ..., n$}
\STATE $J \left(\boldsymbol{\theta}\right) = \dfrac{1}{2m} \sum_{i=1}^{m}{\left(h_{\boldsymbol{\theta}}\left(x^{\left(i\right)}\right) - y^{\left(i\right)}\right)}$
\STATE $\theta_j = \theta_j - \alpha \dfrac{\partial J\left(\boldsymbol{\theta}\right)}{\partial \theta_j}$
\ENDFOR
\ENDFOR
\end{algorithmic}
\end{algorithm}
从上述算法流程中我们可以看到,BGD 算法每次计算梯度都使用了整个训练集,也就是说对于给定的一个初始点,其每一步的更新都是沿着全局梯度最大的负方向。但这同样是其问题,当 $m$ 太大时,整个算法的计算开销就很高了。
SGD
SGD 相比于 BGD,其最主要的区别就在于计算梯度时不再利用整个数据集,而是针对单个样本计算梯度并更新权重,因此,其损失函数定义如下:
$$ J \left(\boldsymbol{\theta}\right) = \dfrac{1}{2} \left(h_{\boldsymbol{\theta}}\left(x^{\left(i\right)}\right) - y^{\left(i\right)}\right) $$
整个算法流程可以表示如下:
\begin{algorithm}
\caption{SGD 算法}
\begin{algorithmic}
\FOR{$epoch = 1, 2, ...$}
\STATE Randomly shuffle dataset
\FOR{$i = 1, 2, ..., m$}
\FOR{$j = 1, 2, ..., n$}
\STATE $J \left(\boldsymbol{\theta}\right) = \dfrac{1}{2} \left(h_{\boldsymbol{\theta}}\left(x^{\left(i\right)}\right) - y^{\left(i\right)}\right)$
\STATE $\theta_j = \theta_j - \alpha \dfrac{\partial J\left(\boldsymbol{\theta}\right)}{\partial \theta_j}$
\ENDFOR
\ENDFOR
\ENDFOR
\end{algorithmic}
\end{algorithm}
SGD 相比于 BGD 具有训练速度快的优势,但同时由于权重改变的方向并不是全局梯度最大的负方向,甚至相反,因此不能够保证每次损失函数都会减小。
MBGD
针对 BGD 和 SGD 的问题,MBGD 则是一个折中的方案,在每次更新参数时,MBGD 会选取 $b$ 个样本计算的梯度,设第 $k$ 批中数据的下标的集合为 $B_k$,则其损失函数定义如下:
$$ \nabla_{\theta_j} = \dfrac{\partial J\left(\boldsymbol{\theta}\right)}{\partial \theta_j} = - \dfrac{1}{|B_k|} \sum_{i \in B_k}{\left(y^{\left(i\right)} - h_{\boldsymbol{\theta}} \left(x^{\left(i\right)}\right)\right) x_j^{\left(i\right)}} $$
整个算法流程可以表示如下:
\begin{algorithm}
\caption{MBGD 算法}
\begin{algorithmic}
\FOR{$epoch = 1, 2, ...$}
\FOR{$k = 1, 2, ..., m / b$}
\FOR{$j = 1, 2, ..., n$}
\STATE $J \left(\boldsymbol{\theta}\right) = \dfrac{1}{|B_k|} \sum_{i \in B_k}{\left(y^{\left(i\right)} - h_{\boldsymbol{\theta}} \left(x^{\left(i\right)}\right)\right) x_j^{\left(i\right)}}$
\STATE $\theta_j = \theta_j - \alpha \dfrac{\partial J\left(\boldsymbol{\theta}\right)}{\partial \theta_j}$
\ENDFOR
\ENDFOR
\ENDFOR
\end{algorithmic}
\end{algorithm}
Momentum
当梯度沿着一个方向要明显比其他方向陡峭,我们可以形象的称之为峡谷形梯度,这种情况多位于局部最优点附近。在这种情况下,SGD 通常会摇摆着通过峡谷的斜坡,这就导致了其到达局部最优值的速度过慢。因此,针对这种情况,Momentum 2 方法提供了一种解决方案。针对原始的 SGD 算法,参数每 $t$ 步的变化量可以表示为
$$ \boldsymbol{v}_t = - \alpha \nabla_{\boldsymbol{\theta}} J \left(\boldsymbol{\theta}_t\right) $$
Momentum 算法则在其变化量中添加了一个动量分量,即
$$ \begin{equation} \begin{split} \boldsymbol{v}_t &= - \alpha \nabla_{\boldsymbol{\theta}} J \left(\boldsymbol{\theta}_t\right) + \gamma \boldsymbol{v}_{t-1} \\ \boldsymbol{\theta}_t &= \boldsymbol{\theta}_{t-1} + \boldsymbol{v}_t \end{split} \end{equation} $$
对于添加的动量项,当第 $t$ 步和第 $t-1$ 步的梯度方向相同时,$\boldsymbol{\theta}$ 则以更快的速度更新;当第 $t$ 步和第 $t-1$ 步的梯度方向相反时,$\boldsymbol{\theta}$ 则以较慢的速度更新。利用 SGD 和 Momentum 两种方法,在峡谷行的二维梯度上更新参数的示意图如下所示
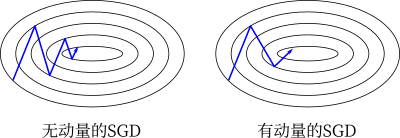
NAG
NAG (Nesterov Accelerated Gradient) 3 是一种 Momentum 算法的变种,其核心思想会利用“下一步的梯度”确定“这一步的梯度”,当然这里“下一步的梯度”并非真正的下一步的梯度,而是指仅根据动量项更新后位置的梯度。Sutskever 4 给出了一种更新参数的方法:
$$ \begin{equation} \begin{split} \boldsymbol{v}_t &= - \alpha \nabla_{\boldsymbol{\theta}} J \left(\boldsymbol{\theta}_t + \gamma \boldsymbol{v}_{t-1}\right) + \gamma \boldsymbol{v}_{t-1} \\ \boldsymbol{\theta}_t &= \boldsymbol{\theta}_{t-1} + \boldsymbol{v}_t \end{split} \end{equation} $$
针对 Momentum 和 NAG 两种不同的方法,其更新权重的差异如下图所示:
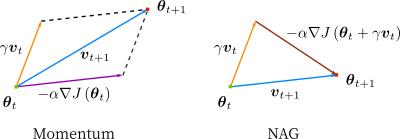
AdaGrad
AdaGrad 5 是一种具有自适应学习率的的方法,其对于低频特征的参数选择更大的更新量,对于高频特征的参数选择更小的更新量。因此,AdaGrad算法更加适用于处理稀疏数据。Pennington 等则利用该方法训练 GloVe 6 词向量,因为对于出现次数较少的词应当获得更大的参数更新。
因为每个参数的学习速率不再一样,则在 $t$ 时刻第 $i$ 个参数的变化为
$$ \theta_{t, i} = \theta_{t-1, i} - \alpha \nabla_{\theta} J \left(\theta_{t-1, i}\right) $$
根据 AdaGrad 方法的更新方式,我们对学习率做出如下变化
$$ \theta_{t, i} = \theta_{t-1, i} - \dfrac{\alpha}{\sqrt{G_{t, i}} + \epsilon} \nabla_{\theta} J \left(\theta_{t-1, i}\right) $$
其中,$G_t$ 表示截止到 $t$ 时刻梯度的平方和;$\epsilon$ 为平滑项,防止除数为零,一般设置为 $10^{-8}$。AdaGrad 最大的优势就在于其能够自动调节每个参数的学习率。
Adadelta
上文中 AdaGrad 算法存在一个缺点,即其用于调节学习率的分母中包含的是一个梯度的平方累加项,随着训练的不断进行,这个值将会越来越大,也就是说学习率将会越来越小,最终导致模型不会再学习到任何知识。Adadelta 7 方法针对 AdaGrad 的这个问题,做出了进一步改进,其不再计算历史所以梯度的平方和,而是使用一个固定长度 $w$ 的滑动窗口内的梯度。
因为存储 $w$ 的梯度平方并不高效,Adadelta 采用了一种递归的方式进行计算,定义 $t$ 时刻梯度平方的均值为
$$ E \left[g^2\right]_t = \rho E \left[g^2\right]_{t-1} + \left(1 - \rho\right) g^2_{t} $$
其中,$g_t$ 表示 $t$ 时刻的梯度;$\rho$ 为一个衰减项,类似于 Momentum 中的衰减项。在更新参数过程中我们需要其平方根,即
$$ \text{RMS} \left[g\right]_t = \sqrt{E \left[g^2\right]_t + \epsilon} $$
则参数的更新量为
$$ \Delta \theta_t = - \dfrac{\alpha}{\text{RMS} \left[g\right]_t} g_t $$
除此之外,作者还考虑到上述更新中更新量和参数的假设单位不一致的情况,在上述更新公式中添加了一个关于参数的衰减项
$$ \text{RMS} \left[\Delta \theta\right]_t = \sqrt{E \left[\Delta \theta^2\right]_t + \epsilon} $$
其中
$$ E \left[\Delta \theta^2\right]_t = \rho E \left[\Delta \theta^2\right]_{t-1} + \left(1 - \rho\right) \Delta \theta_t^2 $$
在原始的论文中,作者直接用 $\text{RMS} \left[\Delta \theta^2\right]_t$ 替换了学习率,即
$$ \Delta \theta_t = - \dfrac{\text{RMS} \left[\Delta \theta\right]_{t-1}}{\text{RMS} \left[g\right]_t} g_t $$
而在 Keras 源码中,则保留了固定的学习率,即
$$ \Delta \theta_t = - \alpha \dfrac{\text{RMS} \left[\Delta \theta\right]_{t-1}}{\text{RMS} \left[g\right]_t} g_t $$
RMSprop
RMSprop 8 是由 Hinton 提出的一种针对 AdaGrad 的改进算法。参数的更新量为
$$ \Delta \theta_t = - \dfrac{\alpha}{\text{RMS} \left[g\right]_t} g_t $$
Adam
Adam (Adaptive Moment Estimation) 9 是另一种类型的自适应学习率方法,类似 Adadelta,Adam 对于每个参数都计算各自的学习率。Adam 方法中包含一个一阶梯度衰减项 $m_t$ 和一个二阶梯度衰减项 $v_t$
$$ \begin{equation} \begin{split} m_t &= \beta_1 m_{t-1} + \left(1 - \beta_1\right) g_t \\ v_t &= \beta_2 v_{t-1} + \left(1 - \beta_2\right) g_t^2 \end{split} \end{equation} $$
算法中,$m_t$ 和 $v_t$ 初始化为零向量,作者发现两者会更加偏向 $0$,尤其是在训练的初始阶段和衰减率很小的时候 (即 $\beta_1$ 和 $\beta_2$ 趋近于1的时候)。因此,对其偏差做如下校正
$$ \begin{equation} \begin{split} \hat{m}_t &= \dfrac{m_t}{1 - \beta_1^t} \\ \hat{v}_t &= \dfrac{v_t}{1 - \beta_2^t} \end{split} \end{equation} $$
最终得到 Adam 算法的参数更新量如下
$$ \Delta \theta = - \dfrac{\alpha}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t $$
Adamax
在 Adam 中参数的更新方法利用了 $L_2$ 正则形式的历史梯度 ($v_{t-1}$) 和当前梯度 ($|g_t|^2$),因此,更一般的,我们可以使用 $L_p$ 正则形式,即
$$ \begin{equation} \begin{split} v_t &= \beta_2^p v_{t-1} + \left(1 - \beta_2^p\right) |g_t|^p \\ &= \left(1 - \beta_2^p\right) \sum_{i=1}^{t} \beta_2^{p\left(t-i\right)} \cdot |g_t|^p \end{split} \end{equation} $$
这样的变换对于值较大的 $p$ 而言是很不稳定的,但对于极端的情况,当 $p$ 趋近于无穷的时候,则变为了一个简单并且稳定的算法。则在 $t$ 时刻对应的我们需要计算 $v_t^{1/p}$,令 $u_t = \lim_{p \to \infty} \left(v_t\right)^{1/p}$,则有
$$ \begin{equation} \begin{split} u_t &= \lim_{p \to \infty} \left(\left(1 - \beta_2^p\right) \sum_{i=1}^{t} \beta_2^{p\left(t-i\right)} \cdot |g_t|^p\right)^{1/p} \\ &= \lim_{p \to \infty} \left(1 - \beta_2^p\right)^{1/p} \left(\sum_{i=1}^{t} \beta_2^{p\left(t-i\right)} \cdot |g_t|^p\right)^{1/p} \\ &= \lim_{p \to \infty} \left(\sum_{i=1}^{t} \beta_2^{p\left(t-i\right)} \cdot |g_t|^p\right)^{1/p} \\ &= \max \left(\beta_2^{t-1} |g_1|, \beta_2^{t-2} |g_2|, ..., \beta_{t-1} |g_t|\right) \end{split} \end{equation} $$
写成递归的形式,则有
$$ u_t = \max \left(\beta_2 \cdot u_{t-1}, |g_t|\right) $$
则 Adamax 算法的参数更新量为
$$ \Delta \theta = - \dfrac{\alpha}{u_t} \hat{m}_t $$
Nadam
Adam 算法可以看做是对 RMSprop 和 Momentum 的结合:历史平方梯度的衰减项 $v_t$ (RMSprop) 和 历史梯度的衰减项 $m_t$ (Momentum)。Nadam (Nesterov-accelerated Adaptive Moment Estimation) 10 则是将 Adam 同 NAG 进行了进一步结合。我们利用 Adam 中的符号重新回顾一下 NAG 算法
$$ \begin{equation} \begin{split} g_t &= \nabla_{\theta} J \left(\theta_t - \gamma m_{t-1}\right) \\ m_t &= \gamma m_{t-1} + \alpha g_t \\ \theta_t &= \theta_{t-1} - m_t \end{split} \end{equation} $$
NAG 算法的核心思想会利用“下一步的梯度”确定“这一步的梯度”,在 Nadam 算法中,作者在考虑“下一步的梯度”时对 NAG 进行了改动,修改为
$$ \begin{equation} \begin{split} g_t &= \nabla_{\theta} J \left(\theta_t\right) \\ m_t &= \gamma m_{t-1} + \alpha g_t \\ \theta_t &= \theta_{t-1} - \left(\gamma m_t + \alpha g_t\right) \end{split} \end{equation} $$
对于 Adam,根据
$$ \hat{m}_t = \dfrac{\beta_1 m_{t-1}}{1 - \beta_1^t} + \dfrac{\left(1 - \beta_1\right) g_t}{1 - \beta_1^t} $$
则有
$$ \begin{equation} \begin{split} \Delta \theta &= - \dfrac{\alpha}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t \\ &= - \dfrac{\alpha}{\sqrt{\hat{v}_t} + \epsilon} \left(\dfrac{\beta_1 m_{t-1}}{1 - \beta_1^t} + \dfrac{\left(1 - \beta_1\right) g_t}{1 - \beta_1^t}\right) \end{split} \end{equation} $$
上式中,仅 $\dfrac{\beta_1 m_{t-1}}{1 - \beta_1^t}$ 和动量项相关,因此我们类似上文中对 NAG 的改动,通过简单的替换加入 Nesterov 动量项,最终得到 Nadam 方法的参数的更新量
$$ \Delta \theta = - \dfrac{\alpha}{\sqrt{\hat{v}_t} + \epsilon} \left(\dfrac{\beta_1 m_{t-1}}{1 - \beta_1^{t+1}} + \dfrac{\left(1 - \beta_1\right) g_t}{1 - \beta_1^t}\right) $$
AMSGrad
对于前面提到的 Adadelta,RMSprop,Adam 和 Nadam 方法,他们均采用了平方梯度的指数平滑平均值迭代产生新的梯度,但根据观察,在一些情况下这些算法并不能收敛到最优解。Reddi 等提出了一种新的 Adam 变体算法 AMSGrad 11,在文中作者解释了为什么 RMSprop 和 Adam 算法无法收敛到一个最优解的问题。通过分析表明,为了保证得到一个收敛的最优解需要保留过去梯度的“长期记忆”,因此在 AMSGrad 算法中使用了历史平方梯度的最大值而非滑动平均进行更新参数,即
$$ \begin{equation} \begin{split} m_t &= \beta_1 m_{t-1} + \left(1 - \beta_1\right) g_t \\ v_t &= \beta_2 v_{t-1} + \left(1 - \beta_2\right) g_t^2 \\ \hat{v}_t &= \max \left(\hat{v}_{t-1}, v_t\right) \\ \Delta \theta &= - \dfrac{\alpha}{\sqrt{\hat{v}_t} + \epsilon} m_t \end{split} \end{equation} $$
作者在一些小数据集和 CIFAR-10 数据集上得到了相比于 Adam 更好的效果,但与此同时一些其他的 实验 却得到了相比与 Adam 类似或更差的结果,因此对于 AMSGrad 算法的效果还有待进一步确定。
算法可视化
正所谓一图胜千言,Alec Radford 提供了 2 张图形象了描述了不同优化算法之间的区别
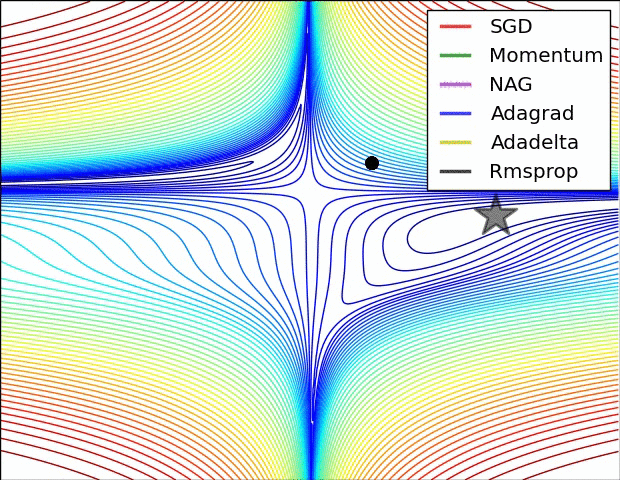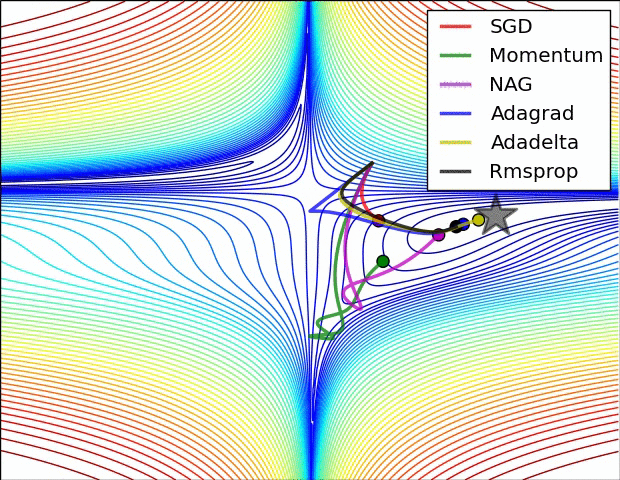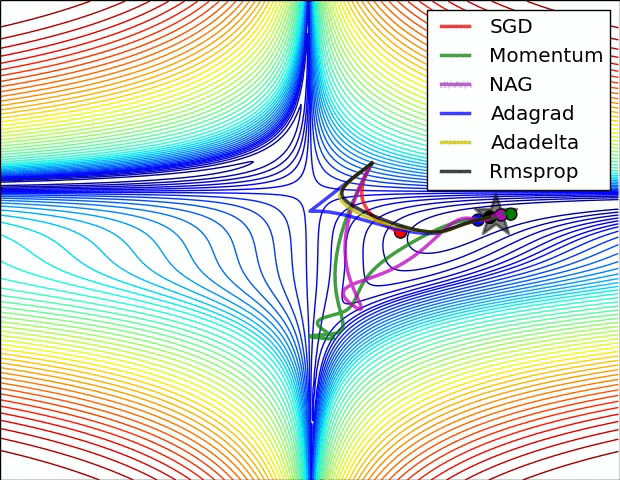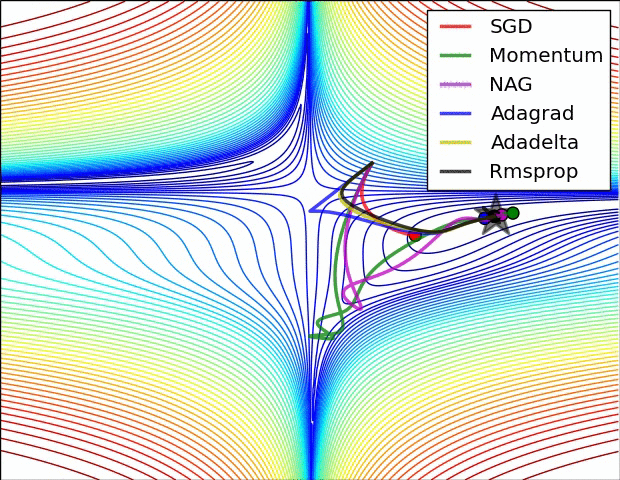
左图为 Beale Function 在二维平面上的等高线,从图中可以看出 AdaGrad,Adadelta 和 RMSprop 算法很快的找到正确的方向并迅速的收敛到最优解;Momentum 和 NAG 则在初期出现了偏离,但偏离之后调整了方向并收敛到最优解;而 SGD 尽管方向正确,但收敛速度过慢。
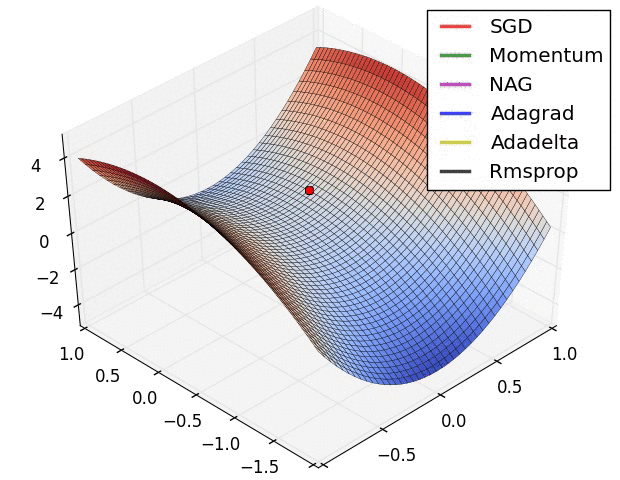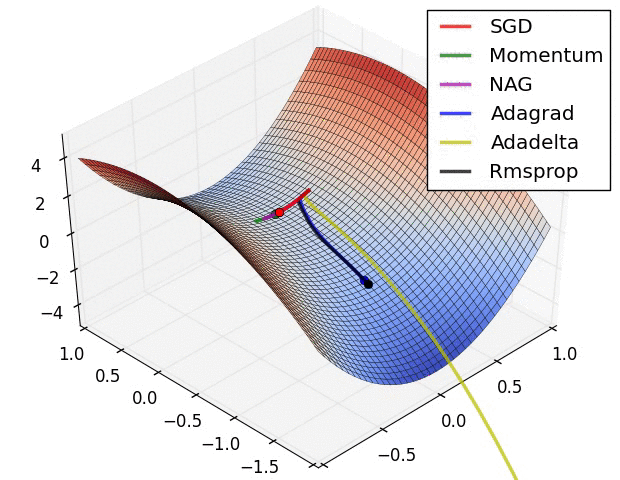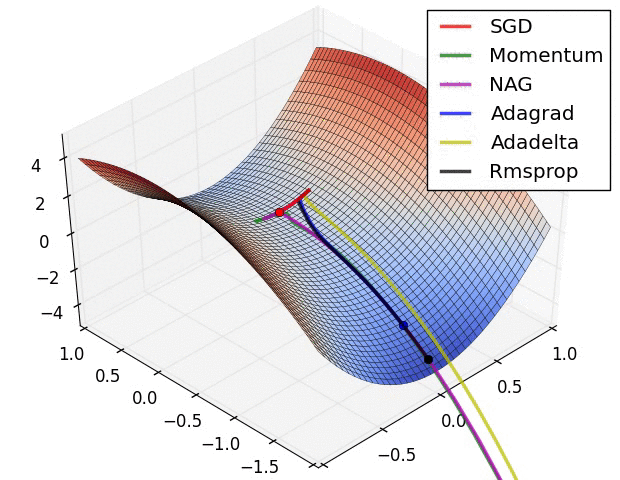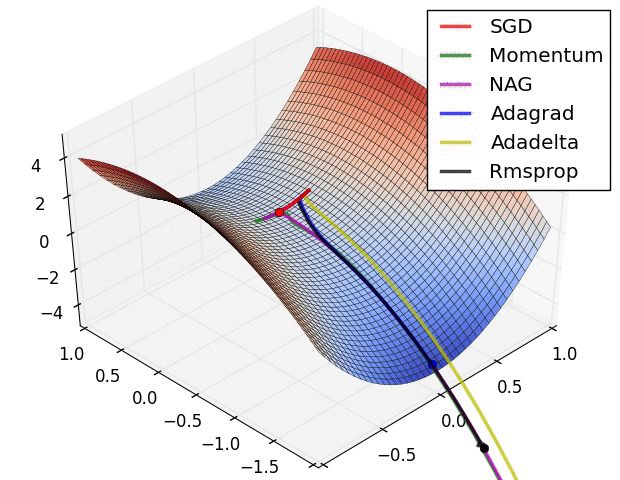
右图为包含鞍点的一个三维图像,图像函数为 $z = x^2 - y^2$,从图中可以看出 AdaGrad,Adadelta 和 RMSprop 算法能够相对很快的逃离鞍点,而 Momentum,NAG 和 SGD 则相对比较困难逃离鞍点。
很不幸没能找到 Alec Radford 绘图的原始代码,不过 Louis Tiao 在 博客 中给出了绘制类似动图的方法。因此,本文参考该博客和 Keras 源码中对不同优化算法的实现重新绘制了 2 张类似图像,详细过程参见 源代码,动图如下所示:

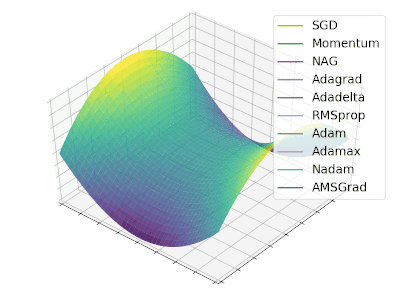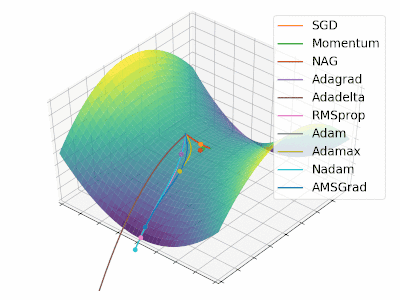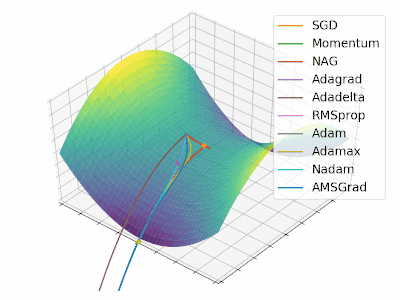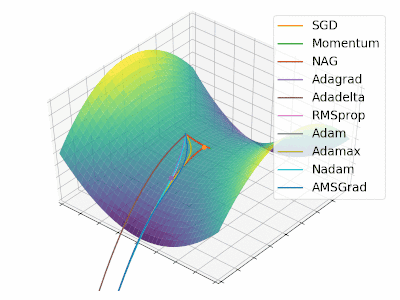
-
Ruder, Sebastian. “An overview of gradient descent optimization algorithms.” arXiv preprint arXiv:1609.04747 (2016). ↩︎
-
Qian, Ning. “On the momentum term in gradient descent learning algorithms.” Neural networks 12.1 (1999): 145-151. ↩︎
-
Nesterov, Yurii. “A method for unconstrained convex minimization problem with the rate of convergence O (1/k^2).” Doklady AN USSR. Vol. 269. 1983. ↩︎
-
Sutskever, Ilya. “Training recurrent neural networks.” University of Toronto, Toronto, Ont., Canada (2013). ↩︎
-
Duchi, John, Elad Hazan, and Yoram Singer. “Adaptive subgradient methods for online learning and stochastic optimization.” Journal of Machine Learning Research 12.Jul (2011): 2121-2159. ↩︎
-
Pennington, Jeffrey, Richard Socher, and Christopher Manning. “Glove: Global vectors for word representation.” Proceedings of the 2014 conference on empirical methods in natural language processing (EMNLP). 2014. ↩︎
-
Zeiler, Matthew D. “ADADELTA: an adaptive learning rate method.” arXiv preprint arXiv:1212.5701 (2012). ↩︎
-
Hinton, G., Nitish Srivastava, and Kevin Swersky. “Rmsprop: Divide the gradient by a running average of its recent magnitude.” Neural networks for machine learning, Coursera lecture 6e (2012). ↩︎
-
Kingma, Diederik P., and Jimmy Ba. “Adam: A method for stochastic optimization.” arXiv preprint arXiv:1412.6980 (2014). ↩︎
-
Dozat, Timothy. “Incorporating nesterov momentum into adam.” (2016). ↩︎
-
Reddi, Sashank J., Satyen Kale, and Sanjiv Kumar. “On the convergence of adam and beyond.” International Conference on Learning Representations. 2018. ↩︎