手中有刀，心里有佛

流形学习 (Manifold Learning)

范叶亮 / 2018-03-16

分类: 机器学习, 表示学习 / 标签: 流行学习, Manifold Learning, 降维, Dimensionality Reduction, ISOMAP, LLE, LE, LTSA, MDS / 字数: 6206

降维

在之前的 博客 中，我们曾经介绍过 PCA 方法及其降维的作用。在原始数据中各个特征之间存在着一定的信息冗余，随着特征的不断增加就容易出现“维数灾难”的问题，因此降维的目的就是在尽可能多的保留原始信息的同时减少数据的维度。一般情况下我们将降维方法分为：线性降维方法和非线性降维方法，线性降维方法的典型算法有：

非线性降维方法中在此我们仅列举一些基于流行学习的算法：

在现实数据中，很多情况数据是无法通过线性的方法进行降维表示的，因此就需要非线性的降维算法出马了。

流形

在调研流形相关概念时，发现要想深一步的理解这些概念还是需要详细的了解微分几何相关的内容，鉴于本文的目的主要是介绍流形学习 (主要是降维角度) 的相关内容，因此我们对流形仅做一些粗略的介绍。

“流形”是英文单词 Manifold 的中文译名，它源于德文术语 Mannigfaltigkeit，最早出现在 Riemann 1851 年的博士论文中，用来表示某种属性所能取到的所有值 7。为了更好的理解流形，我们先引入几个概念：

拓扑结构 (拓扑) 任意给定集合 $X$ 上的一个拓扑结构 (拓扑) 是 $X$ 的某些特定子集组成的集合 $\tau \subset 2^X$，其中那些特定子集称为 $\tau$ 所声明的开集，同时满足如下性质：

  1. 空集和全集是开集，即 $\varnothing, X \in \tau$
  2. 任意多个开集的并集是开集
  3. 有限多个开集的交集是开集

拓扑空间 指定了拓扑结构的集合就称为一个拓扑空间。

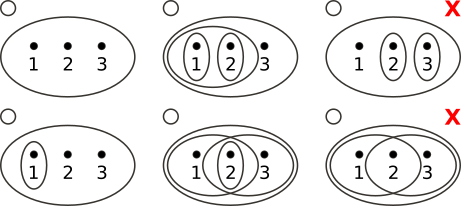
上图中给出了一些拓扑空间的示例，其中左侧 4 个为正确示例，右侧 2 个为错误示例。右上角的缺少了 {2} 和 {3} 的并集 {2, 3}，右下角的缺少了 {1, 2} 和 {2, 3} 的交集 {2}。

同胚 两个拓扑空间 $\left(X, \tau_X\right)$ 和 $\left(Y, \tau_Y\right)$ 之间的函数 $f: X \to Y$ 称为同胚，如果它具有下列性质：

  1. $f$ 是双射 (单射和满射)
  2. $f$ 是连续的
  3. 反函数 $f^{−1}$ 也是连续的 ($f$ 是开映射)

如果拓扑空间是一个几何物体，同胚就是把物体连续延展和弯曲，使其成为一个新的物体。因此，正方形和圆是同胚的，但球面和环面就不是。用一幅图形象的理解同胚，例如下图所示的咖啡杯和甜甜圈 8：

最后我们回过头来解释到底什么是流形？流形并不是一个“形状”，而是一个“空间” 9。最容易定义的流形是拓扑流形，它局部看起来象一些“普通”的欧几里得空间 $\mathbb{R}^n$，一个拓扑流形是一个局部同胚于一个欧几里得空间的拓扑空间。根据 Whitney 嵌入理论 10，任何一个流形都可以嵌入到高维的欧氏空间中。例如，地球的表面可以理解为一个嵌入 3 维空间的 2 维流形，其局部同胚于 2 维的欧式空间，对于一个球体的表面，用极坐标的形式可以表示为

$$ \begin{equation} \begin{split} x &= r \sin \theta \cos \phi \\ y &= r \sin \theta \sin \phi \\ z &= r \cos \theta \end{split} \end{equation} $$

也就是说其 3 个维度实际上是由 2 个变量控制的。

流形学习

假设 $Y$ 为一个欧式空间 $\mathbb{R}^d$ 的一个 $d$ 维流形，$f: Y \to \mathbb{R}^D$ 为一个光滑嵌入，对于 $D > d$，流形学习的目的就是根据空间 $\mathbb{R}^D$ 中的观测数据 $\{x_i\}$ 重构 $Y$ 和 $f$ 的过程。隐含数据 $\{y_i\}$ 由 $Y$ 随机生成，通过光滑嵌入 $f$ 生成观测数据，即 $\{x_i = f\left(y_i\right)\}$，所以我们可以将流形学习的问题看做是对于一个给定的观测数据一个生成模型的反向过程 11。

在介绍具体的流形学习算法前，我们先引入几个 3 维数据用于解释后续的具体算法

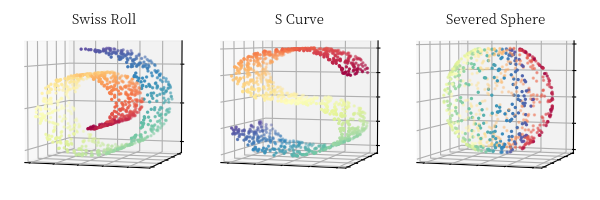
第一个为瑞士卷 (Swiss Roll)，其形状和我们日常生活中的瑞士卷相似；第二个为 S 形曲线 (S Curve)；第三个为一个被切断的球面 (Severed Sphere)。

MDS

多尺度变换 (MDS, Multi-Dimensional Scaling) 3 是一种通过保留样本在高维空间中的不相似性 (Dissimilarity) 降低数据维度的方法，在这里不相似性可以理解为样本之间的距离。因此，根据距离的度量方式不同可以将其分为度量型 (metric) MDS 和 非度量型 (non-metric) MDS。度量型 MDS 通过计算不同样本之间距离的度量值进行降维，而非度量型则仅考虑距离的排序信息，在此我们仅对度量型 MDS 做简单介绍。

MDS 的目标是保留样本在高维空间中的不相似性，假设 $x \in \mathbb{R}^D, x' \in \mathbb{R}^d, D > d$，则 MDS 的目标函数可以写为

$$ \min \sum_{i, j} \lvert dist \left(x_i, x_j\right) - dist \left(x'_i, x'_j\right) \rvert $$

则，度量型 MDS 的算法的步骤如下：

  1. 计算样本的距离矩阵 $\boldsymbol{D} = \left[d_{i, j}\right] = \left[dist \left(x_i, x_j\right)\right]$。
  2. 构造矩阵 $\boldsymbol{A} = \left[a_{i, j}\right] = \left[- \dfrac{1}{2} d_{i, j}^2\right]$。
  3. 通过中心矫正的方法构造矩阵 $\boldsymbol{B} = \boldsymbol{J} \boldsymbol{D} \boldsymbol{J}, \boldsymbol{J} = \boldsymbol{I} - \dfrac{1}{n} \boldsymbol{O}$，其中 $\boldsymbol{I}$ 为 $n \times n$ 的单位阵，$\boldsymbol{O}$ 为 $n \times n$ 的值均为 $1$ 的矩阵。
  4. 计算矩阵 $\boldsymbol{B}$ 的特征向量 $e_1, e_2, ..., e_m$ 及其对应的特征值 $\lambda_1, \lambda_2, ..., \lambda_m$。
  5. 确定维度 $k$，重构数据 $\boldsymbol{X}' = \boldsymbol{E}_k \boldsymbol{\Lambda}_k^{1/2}$，其中 $\boldsymbol{\Lambda}_k$ 为前 $k$ 个值最大的 $k$ 个特征值构成的对角矩阵，$\boldsymbol{E}_k$ 是对应的 $k$ 个特征向量构成的矩阵。

在《多元统计分析》12一书中证明了，$\boldsymbol{X}$ 的 $k$ 维主坐标正好是将 $\boldsymbol{X}$ 中心化后 $n$ 个样本的前 $k$ 个主成份的值，由此可见 MDS 和 PCA 的作用是类似的。

我们利用中国省会的地理位置给出 MDS 的一个示例，首先我们获取中国省会共 34 个点的坐标，其次我们计算两两之间的距离，我们仅利用距离信息利用 MDS 还原出 2 维空间中的坐标，可视化结果如下所示

其中，黑色的点为省会的真实位置，蓝色的点为利用距离矩阵和 MDS 还原出来的位置，为了绘制还原出的位置我们对 MDS 的结果做出了适当的翻转和变换。从结果中不难看出，尽管每个点的坐标相比真实坐标都有一定的偏离，但是其很好的保持了相对距离，这也正是 MDS 算法的要求。

ISOMAP

对于一些非线性的流形，如果使用线性的降维方法得到的效果就不尽人意了，例如上文中提到的瑞士卷。在 ISOMAP 中，我们首先引入一个测地线的概念，在距离度量定义时，测地线可以定义为空间中两点的局域最短路径。形象的，在一个球面上，两点之间的测地线就是过这两个点的大圆的弧线

那么，对于非线性流形，ISOMAP 则是通过构建邻接图，利用图上的最短距离来近似测地线。在构造邻接图时，我们使用最近邻算法，对于一个点 $x_i$ 连接距离其最近的 $k$ 个点，两点之间的距离我们则一般使用传统的欧式距离。则任意两点之间的测地线距离则可以利用构建的邻接图上的最短路径进行估计，图上的最短路问题我们可以通过 Dijkstra 或 Floyd-Warshall 算法计算。得到样本的距离矩阵后，ISOMAP 算法则使用 MDS 方法计算得到低维空间的座标映射。

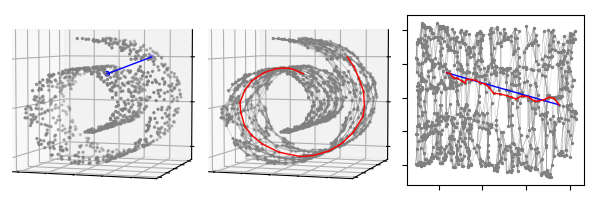
上图中，我们给出了利用 ISOMAP 对瑞士卷降至 2 维的一个格式化过程。第一幅图中，我们标注了 2 个蓝色的点，其中蓝色的直线为这 2 个点在三维空间中的欧式距离。第二幅图中，同样是相同的两个点，我们首先利用最近邻算法 ($k = 10$) 将瑞士卷所有的点连接为一个邻接图，其中红色的路径为这 2 个点在邻接图上的最短路。第三幅图是通过 ISOMAP 算法降维至 2 维的结果，其中蓝色的直线是这两个点在 2 维空间中的欧式距离，红色的路径是 3 维最短路在 2 维结果中的连线，可以看出两者是很相近的。

LLE

局部线性嵌入 (LLE, Locally Linear Embedding) 5，从这个名称上我们不难看出其不同与 ISOMAP 那种通过都建邻接图保留全局结构的，而是从局部结构出发对数据进行降维。在 LLE 方法中，主要有如下的基本假设：

基于上面的假设，LLE 算法的流程如下：

  1. 对于点 $X_i$，计算距离其最近的 $k$ 个点，$X_j, j \in N_i$。
  2. 计算权重 $W_{ij}$ 是的能够通过点 $X_i$ 的邻居节点最优的重构该点，即最小化 $$ \epsilon \left(W\right) = \sum_i \left\lVert X_i - \sum_j W_{ij} X_j \right\rVert ^2 $$
  3. 通过权重 $W_{ij}$ 计算 $X$ 的低维最优重构 $Y$，即最小化 $$ \phi \left(Y\right) = \sum_i \left\lVert Y_i - \sum_j W_{ij} Y_j \right\rVert ^2 $$

具体上述问题的优化求解过程在此就不在详细描述。针对 LLE 算法，后续很多人从不同方面对其进行了改进：

  1. Hessian LLE 13 在局部中不再考虑局部的线性关系，而是保持局部的 Hessian 矩阵的二次型的关系。
  2. Modified LLE 14 则是修改了寻找最临近的 $k$ 个样本的方案，其在寻找 $k$ 近邻时希望找到的近邻尽量分布在样本的各个方向，而不是集中在一侧。
  3. LTSA (Local Tangent Space Alignment) 15 则是除了保留了局部的几何性质，同时使用的一个从局部几何到整体性质过渡的 alignment 方法，因此可以理解为是一个局部和整体的组合。

LE

LE (Laplacian Eigenmap) 6 的基本思想是认为在高维空间中距离近的点映射到低维空间中后其位置也相距很近。LE 从这个思想出发，最终将问题转化为求解图拉普拉斯算子的广义特征值问题，具体的一些证明不在这里详细展开说明，具体请参见原文，下面仅给出 LE 算法的流程：

  1. 构建邻接图。
  2. 构建邻接矩阵 $W$，构建邻接矩阵有两种方法：对于点 $i$ 和点 $j$ 相连，如果利用 Hear Kernel (参数 $t \in \mathbb{R}$)，则令 $W_{ij} = \exp \left(\dfrac{- \left\lVert x_i - x_j \right\rVert ^ 2}{t}\right)$；如果使用简介方案，则令 $W_{ij} = 1$，对于不相连的点，则令 $W_{ij} = 0$。
  3. 进行特征映射，通过上面构造的图 $G$，计算如下广义特征值和特征向量 $$ L f = \lambda D f $$ 其中 $D$ 是一个对角矩阵，$D_{ii} = \sum_{j} W_{ji}$，$L = D - W$ 即为拉普拉斯矩阵。对于上式的解 $f_0, .., f_{k-1}$ 为根据特征值从小到大的排序，其中 $0 = \lambda_0 \leq \lambda_1 \leq ... \leq \lambda_{k-1}$，则降维至 $d$ 维的后的特征即为 $\left(f_1, f_2, ..., f_d\right)$。

SNE 和 t-SNE

SNE

SNE (Stochastic Neighbor Embedding) 16 是由 Hinton 等人提出的一种降维算法，其方法的基本假设如下：

  1. 对象之间的相似度可以用概率进行表示，即：相似的对象有更高的概率被同时选择，不相似的对象有较低的概率被同时选择。
  2. 在高维空间中构建的这种概率分布应该尽可能的同低维空间中的概率分布相似。

对于两个点 $x_i, x_j$，假设 $x_i$ 以条件概率 $p_{j∣i}$ 选择 $x_j$ 作为它的邻近点，因此如果两者距离更近 (更相似)，则概率值越大，反之概率值越小，则我们定义 $p_{j∣i}$ 如下：

$$ p_{j∣i} = \dfrac{\exp \left(\dfrac{- \left\lVert x_i - x_j \right\rVert ^ 2}{2 \sigma_i^2}\right)}{\sum_{k \neq i} \exp \left(\dfrac{- \left\lVert x_i - x_k \right\rVert ^ 2}{2 \sigma_i^2}\right)} $$

其中，$\sigma_i$ 为参数，同时我们设置 $p_{i∣i} = 0$，因为我们仅需衡量不同对象之间的相似度。

类似的，根据 SNE 的基本思想，当数据被映射到低维空间中后，其概率分布应同高维空间中的分布尽可能的相似，假设点 $x_i, x_j$ 在低维空间中的映射点为 $y_i, y_j$，则在低维空间中的条件概率 $q_{j∣i}$ 定义为：

$$ q_{j∣i} = \dfrac{\exp \left(- \left\lVert y_i - y_j \right\rVert ^ 2\right)}{\sum_{k \neq i} \exp \left(- \left\lVert y_i - y_k \right\rVert ^ 2\right)} $$

同样，我们设置 $q_{i∣i} = 0$。从 SNE 的基本假设出发，我们的目的是使得数据在高维空间中的条件概率尽可能的和其在低维空间中的条件概率相同，因此对于全部点样本点而言，就是保证高维空间的概率分布 $P_i$ 和低维空间的概率分布 $Q_i$ 尽量形同。在这里我们利用 KL 散度衡量这两个概率分布的差异，则 SNE 的损失函数可以写为：

$$ C = \sum_{i} KL \left(P_i \Vert Q_i\right) = \sum_{i} \sum_{j} p_{j∣i} \log \dfrac{p_{j∣i}}{q_{j∣i}} $$

因为 KL 散度具有不对称性可知，当在原始空间中两点距离较远而降维后的空间中距离较近 (即，$q_{j|i} < p_{j|i}$) 时，会产生较大的 cost，相反则会产生较小的 cost。正是这种不对称性的损失函数导致了 SNE 算法更加关注局部结构，相比忽略了全局结构。

上文中，对于不同的点，$\sigma_i$ 具有不同的值，SNE 算法利用困惑度 (Perplexity) 对其进行优化寻找一个最佳的 $\sigma$，对于一个随机变量 $P_i$，困惑度定义如下：

$$ Perp \left(P_i\right) = 2^{H \left(P_i\right)} $$

其中，$H \left(P_i\right) = \sum_{j} p_{j|i} \log_2 p_{j|i}$ 表示 $P_i$ 的熵。困惑度可以解释为一个点附近的有效近邻点个数。SNE 对困惑度的调整比较有鲁棒性，通常选择 5-50 之间，给定之后，使用二分搜索的方式寻找合适的 $\sigma$。

SNE 的损失函数对 $y_i$ 求梯度后，可得：

$$ \dfrac{\delta C}{\delta y_i} = 2 \sum_j \left(p_{j|i} - q_{j|i} + p_{i|j} - q_{i|j}\right) \left(y_i - y_j\right) $$

t-SNE

SNE 为我们提供了一种很好的降维方法，但是其本身也存在一定的问题，主要有如下两点：

针对这两个问题，Maaten 等人又提出了 t-SNE 算法对其进行优化 17。

针对不对称问题，Maaten 采用的方法是用联合概率分布来替代条件概率分布。高维控件中的联合概率分布为 $P$，低维空间中的联合概率分布为 $Q$，则对于任意的 $i, j$，有 $p_{ij} = p_{ji}, q_{ij} = q_{ji}$，联合概率定义为：

$$ \begin{align} p_{ij} &= \dfrac{\exp \left(\dfrac{- \left\lVert x_i - x_j \right\rVert ^ 2}{2 \sigma^2}\right)}{\sum_{k \neq l} \exp \left(\dfrac{- \left\lVert x_k - x_l \right\rVert ^ 2}{2 \sigma^2}\right)} \\ q_{ij} &= \dfrac{\exp \left(- \left\lVert y_i - y_j \right\rVert ^ 2\right)}{\sum_{k \neq l} \exp \left(- \left\lVert y_k - y_l \right\rVert ^ 2\right)} \end{align} $$

虽然这样保证了对称性，但是对于异常的情况，例如数据点 $x_i$ 在距离群簇较远，则 $\lVert x_i − x_j \rVert ^ 2$ 的值会很大，而 $p_{ij}$ 会相应变得非常小，也就是说 $x_i$ 的位置很远这件事情对损失函数影响很小 (惩罚过小)，那这个点在低维空间中将无法从其他点中区分出来。因此 Maaten 提出了对称的条件概率来重新定义上述联合概率 $p_{ij}$ ，对于数量为 $n$ 的数据点，新的概率公式是：

$$ p_{ij} = \dfrac{p_{j|i} + p_{i|j}}{2n} $$

则损失函数更新为：

$$ C = \sum_{i} KL \left(P_i \Vert Q_i\right) = \sum_{i} \sum_{j} p_{ij} \log \dfrac{p_{ij}}{q_{ij}} $$

梯度更新为：

$$ \dfrac{\delta C}{\delta y_i} = 4 \sum_j \left(p_{ij} - q_{ij}\right) \left(y_i - y_j\right) $$

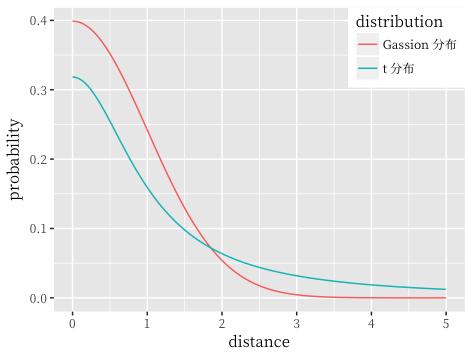
拥挤问题 (Crowding) 就是从高维空间映射到低维空间后，不同类别的簇容易挤在一起，不能很好的地区分开。t-SNE 则是利用了 t 分布重新定义 $q_{ij}$，t 分布具有长尾特性，相比于高斯分布，其在尾部趋向于 0 的速度更慢，对比如图所示：

利用 t 分布重新定义的 $q_{ij}$ 为：

$$ q_{ij} = \dfrac{\left(1 + \lVert y_i - y_j \rVert ^ 2\right) ^ {-1}}{\sum_{k \neq l} \left(1 + \lVert y_k - y_l \rVert ^ 2\right) ^ {-1}} $$

梯度更新为：

$$ \dfrac{\delta C}{\delta y_i} = 4 \sum_j \left(p_{ij} - q_{ij}\right) \left(y_i - y_j\right) \left(1 + \lVert y_i - y_j \rVert ^ 2\right) ^ {-1} $$

利用 t-SNE 对 MNIST 数据集进行降维可视化结果如下：

方法比较

针对上述的若干算法，我们简单列举一下每个算法的优缺点

方法 优点 缺点
Isomap 1. 保持流形的全局几何结构
2. 适用于学习内部平坦的低维流形		 1. 对于数据量较大的情况，计算效率过低
2. 不适于学习有较大内在曲率的流形
LLE 1. 可以学习任意维的局部线性的低维流形
2. 归结为稀疏矩阵特征值计算，计算复杂度相对较小		 1. 所学习的流形只能是不闭合的
2. 要求样本在流形上是稠密采样的
3.对样本中的噪声和邻域参数比较敏感
LE 1. 是局部非线性方法，与谱图理论有很紧密的联系
2. 通过求解稀疏矩阵的特征值问题解析地求出整体最优解，效率非常高
3. 使原空间中离得很近的点在低维空间也离得很近，可以用于聚类		 1. 对算法参数和数据采样密度较敏感
2. 不能有效保持流形的全局几何结构
SNE, t-SNE 1. 非线性降维效果相较上述方法较好 1. 大规模高维数据时，效率显著降低
2. 参数对不同数据集较为敏感

对于瑞士卷 (Swiss Roll)，S 形曲线 (S Curve) 和切断的球面 (Severed Sphere)，我们利用不同的流形算法对其进行降维，可视化的对比结果如下面 3 张图所示，图中同时标注了算法的运行时间，实现主要参照了 scikit-learn 关于流形学习算法的比较 18。

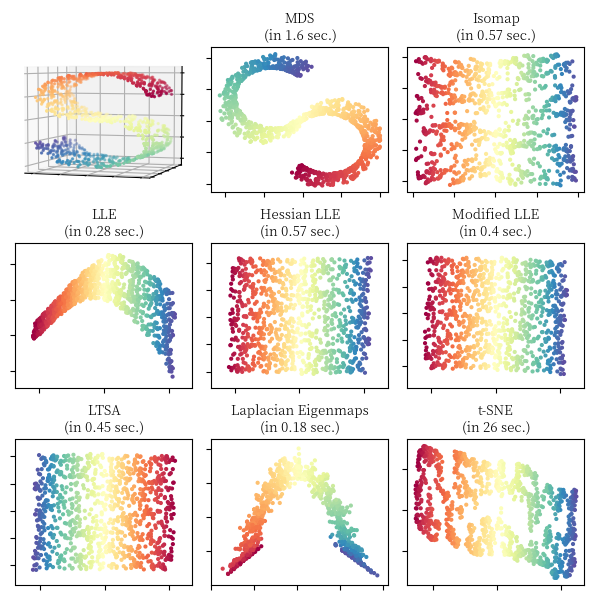
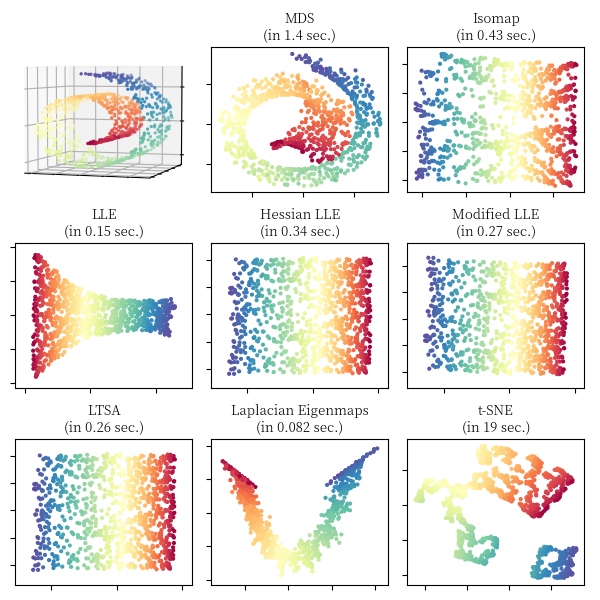
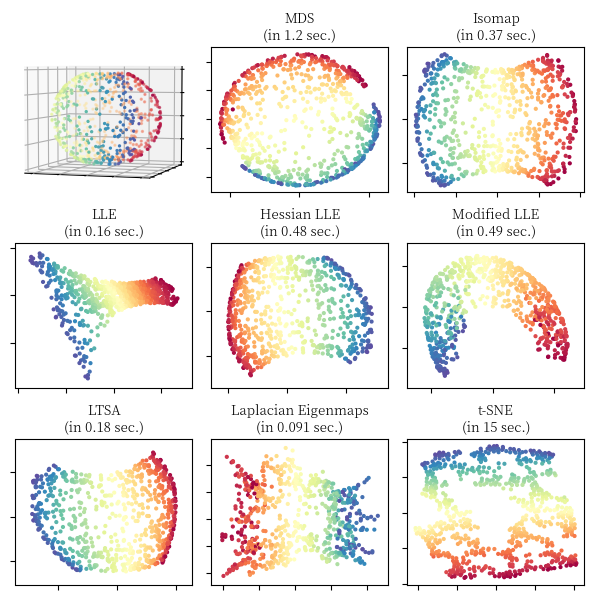
文中相关图片绘制实现详见代码，本文部分内容参考了流形学习专题介绍 19， 流形学习 20，Chrispher 21 的博客和 bingo 22 的博客。

  1. Jolliffe, Ian T. “Principal component analysis and factor analysis.” Principal component analysis. Springer, New York, NY, 1986. 115-128. ↩︎

  2. Balakrishnama, Suresh, and Aravind Ganapathiraju. “Linear discriminant analysis-a brief tutorial.” Institute for Signal and information Processing 18 (1998): 1-8. ↩︎

  3. Cox, Trevor F., and Michael AA Cox. Multidimensional scaling. CRC press, 2000. ↩︎ ↩︎

  4. Tenenbaum, Joshua B., Vin De Silva, and John C. Langford. “A global geometric framework for nonlinear dimensionality reduction.” Science 290.5500 (2000): 2319-2323. ↩︎

  5. Roweis, Sam T., and Lawrence K. Saul. “Nonlinear dimensionality reduction by locally linear embedding.” Science 290.5500 (2000): 2323-2326. ↩︎ ↩︎

  6. Belkin, Mikhail, and Partha Niyogi. “Laplacian eigenmaps for dimensionality reduction and data representation.” Neural computation 15.6 (2003): 1373-1396. ↩︎ ↩︎

  7. 梅加强. 流形与几何初步 ↩︎

  8. https://zh.wikipedia.org/zh-hans/流形 ↩︎

  9. pluskid. 浅谈流形学习 ↩︎

  10. https://en.wikipedia.org/wiki/Whitney_embedding_theorem ↩︎

  11. Silva, Vin D., and Joshua B. Tenenbaum. “Global versus local methods in nonlinear dimensionality reduction.” Advances in neural information processing systems. 2003. ↩︎

  12. 何晓群. 多元统计分析 ↩︎

  13. Donoho, David L., and Carrie Grimes. “Hessian eigenmaps: Locally linear embedding techniques for high-dimensional data.” Proceedings of the National Academy of Sciences 100.10 (2003): 5591-5596. ↩︎

  14. Zhang, Zhenyue, and Jing Wang. “MLLE: Modified locally linear embedding using multiple weights.” Advances in neural information processing systems. 2007. ↩︎

  15. Zhang, Zhenyue, and Hongyuan Zha. “Principal manifolds and nonlinear dimensionality reduction via tangent space alignment.” SIAM journal on scientific computing 26.1 (2004): 313-338. ↩︎

  16. Hinton, Geoffrey E., and Sam T. Roweis. “Stochastic neighbor embedding.” Advances in neural information processing systems. 2003. ↩︎

  17. Maaten, Laurens van der, and Geoffrey Hinton. “Visualizing data using t-SNE.” Journal of machine learning research 9.Nov (2008): 2579-2605. ↩︎

  18. http://scikit-learn.org/stable/auto_examples/manifold/plot_compare_methods.html ↩︎

  19. 王瑞平. 流形学习专题介绍 ↩︎

  20. 何晓飞. 流形学习 ↩︎

  21. http://www.datakit.cn/blog/2017/02/05/t_sne_full.html ↩︎

  22. http://bindog.github.io/blog/2016/06/04/from-sne-to-tsne-to-largevis/ ↩︎