相似性度量 (Similarity Measurement) 用于衡量两个元素之间的相似性程度或两者之间的距离 (Distance)。距离衡量的是指元素之间的不相似性 (Dissimilarity)，通常情况下我们可以利用一个距离函数定义集合 $X$ 上元素间的距离，即：

$$ d: X \times X \to \mathbb{R} $$

同时，对于集合 $X$ 内的元素 $x, y, z$，距离函数一般满足如下条件：

1. $d \left(x, y\right) \geq 0$ (非负性)
2. $d \left(x, y\right) = 0, \text{当且仅当} \ x = y$ (同一性)
3. $d \left(x, y\right) = d \left(y, x\right)$ (对称性)
4. $d \left(x, z\right) \leq d \left(x, y\right) + d \left(y, z\right)$ (三角不等式)

明可夫斯基距离 (明氏距离, Minkowski Distance)

对于点 $x = \left(x_1, x_2, ..., x_n\right)$ 和点 $y = \left(y_1, y_2, ..., y_n\right)$，$p$ 阶明可夫斯基距离 定义为：

$$ d \left(x, y\right) = \left(\sum_{i=1}^{n} |x_i - y_i|^p\right)^{\frac{1}{p}} $$

当 $p = 1$ 时，称之为 曼哈顿距离 (Manhattan Distance) 或 出租车距离：

$$ d \left(x, y\right) = \sum_{i=1}^{n} |x_i - y_i| $$

当 $p = 2$ 时，称之为 欧式距离 (Euclidean Distance) ：

$$ d \left(x, y\right) = \sqrt{\sum_{i=1}^{n} \left(x_i - y_i\right)^2} $$

上图中 绿色 的直线为两点间的欧式距离，红色 黄色 蓝色 的折线均为两点间的曼哈顿距离，不难看出 3 条折线的长度是相同的。

当 $p \to \infty$ 时，称之为 切比雪夫距离 (Chebyshev Distance) ：

$$ d \left(x, y\right) = \lim_{p \to \infty} \left(\sum_{i=1}^{n} |x_i - y_i|^p\right)^{\frac{1}{p}} = \max_{i=1}^{n} |x_i - y_i| $$

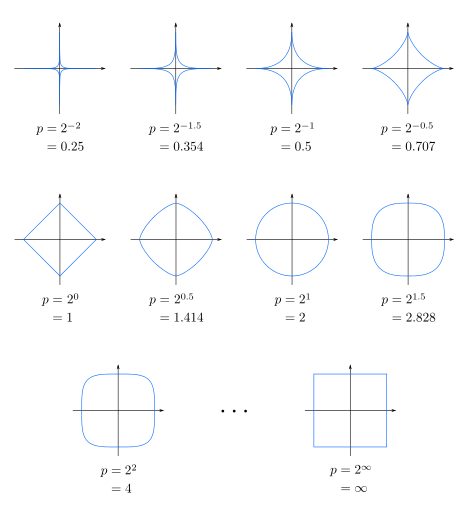
下图展示了不同的 $p$ 值下单位圆，即 $x^p + y^p = 1$，便于大家理解不同 $p$ 值下的明可夫斯基距离：

马哈拉诺比斯距离 (马氏距离, Mahalanobis Distance)

马哈拉诺比斯距离表示数据的 协方差距离，与欧式距离不同其考虑到各种特性之间的联系是 尺度无关 (Scale Invariant) 的。对于一个协方差矩阵为 $\sum$ 的变量 $x$ 和 $y$，马氏距离定义为：

$$ d \left(x, y\right) = \sqrt{\left(x - y\right)^{\top} {\sum}^{-1} \left(x - y\right)} $$

马氏距离的最大优势就是其不受不同维度之间量纲的影响，同时引入的问题便是扩大了变化量较小的变量的影响。以下图为例 (源码详见 这里)：

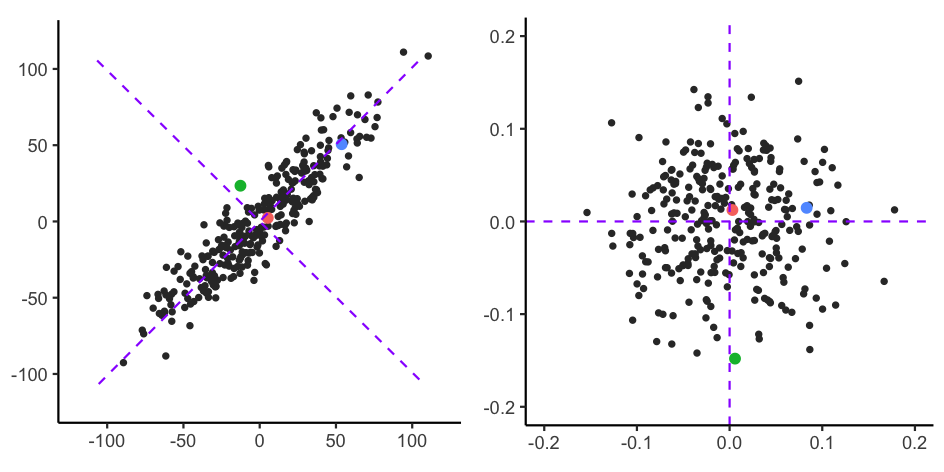
左侧图中根据欧式距离计算，红色 的点距离 绿色 的点更近一些，右侧图是根据马氏距离进行座标变换后的示意图，不难看出此时 红色 的点距离 蓝色 的点更近一些。

向量内积 (Inner Product of Vectors)

在欧几里得几何中，两个笛卡尔坐标向量的点积常称为内积，向量内积是两个向量的长度与它们夹角余弦的积，定义为：

$$ x \cdot y = \sum_{i=1}^{n}{x_i y_i} $$

从代数角度看，先对两个数字序列中的每组对应元素求积，再对所有积求和，结果即为点积。从几何角度看，点积则是两个向量的长度与它们夹角余弦的积。在欧几里得空间中，点积可以直观地定义为：

$$ x \cdot y = \left| x \right| \left| y \right| \cos \theta $$

余弦相似度 (Cosine Similarity) 可以利用两个向量夹角的 cos 值定义，即：

$$ s \left(x, y\right) = \cos \left(\theta\right) = \dfrac{x \cdot y}{\left| x \right| \left| y \right|} = \dfrac{\sum_{i=1}^{n}{x_i y_i}}{\sqrt{\sum_{i=1}^{n}{x_i^2}} \sqrt{\sum_{i=1}^{n}{y_i^2}}} $$

余弦相似度的取值范围为：$\left[-1, 1\right]$，1 表示两者完全正相关，-1 表示两者完全负相关，0 表示两者之间独立。余弦相似度与向量的长度无关，只与向量的方向有关，但余弦相似度会受到向量平移的影响。

皮尔逊相关系数 (Pearson Correlation) 解决了余弦相似度会收到向量平移影响的问题，其定义为：

$$ \rho \left(x, y\right) = \dfrac{\text{cov} \left(x, y\right)}{\sigma_x \sigma_y} = \dfrac{E \left[\left(x - \mu_x\right) \left(y - \mu_y\right)\right]}{\sigma_x \sigma_y} $$

其中，$\text{cov}$ 表示协方差，$E$ 表示期望，$\mu$ 表示均值，$\sigma$ 表示标准差。对于样本的皮尔逊相关系数，可以通过如下方式计算：

$$ \begin{equation} \begin{split} r &= \dfrac{\sum_{i=1}^{n}{\left(x_i - \bar{x}\right) \left(y_i - \bar{y}\right)}}{\sqrt{\sum_{i=1}^{n}{\left(x_i - \bar{x}\right)^2}} \sqrt{\sum_{i=1}^{n}{\left(y_i - \bar{y}\right)^2}}} \\ &= \dfrac{1}{n-1} \sum_{i=1}^{n}{\left(\dfrac{x_i - \bar{x}}{\sigma_x}\right) \left(\dfrac{y_i - \bar{y}}{\sigma_y}\right)} \end{split} \end{equation} $$

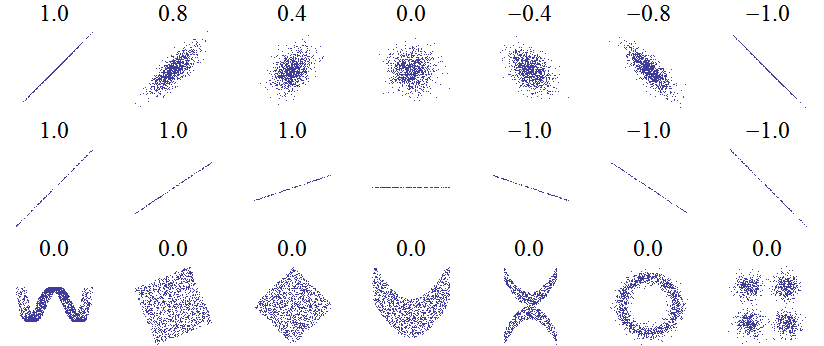
皮尔逊相关系数的取值范围为：$\left[-1, 1\right]$，值的含义与余弦相似度相同。皮尔逊相关系数有一个重要的数学特性是：变量位置和尺度的变化并不会引起相关系数的改变。下图给出了不同的 $\left(x, y\right)$ 之间的皮尔逊相关系数。

集合距离 (Distance of Sets)

对于两个集合之间的相似性度量，主要有如下几种方法：

• Jaccard 系数

$$ s = \dfrac{\left|X \cap Y\right|}{\left| X \cup Y \right|} = \dfrac{\left|X \cap Y\right|}{\left|X\right| + \left|Y\right| - \left|X \cap Y\right|} $$

Jaccard 系数的取值范围为：$\left[0, 1\right]$，0 表示两个集合没有重合，1 表示两个集合完全重合。

• Dice 系数

$$ s = \dfrac{2 \left| X \cap Y \right|}{\left|X\right| + \left|Y\right|} $$

与 Jaccard 系数相同，Dice 系数的取值范围为：$\left[0, 1\right]$，两者之间可以相互转换 $s_d = 2 s_j / \left(1 + s_j\right), s_j = s_d / \left(2 - s_d\right)$。不同于 Jaccard 系数，Dice 系数的差异函数 $d = 1 - s$ 并不是一个合适的距离度量，因为其并不满足距离函数的三角不等式。

• Tversky 系数

$$ s = \dfrac{\left| X \cap Y \right|}{\left| X \cap Y \right| + \alpha \left| X \setminus Y \right| + \beta \left| Y \setminus X \right|} $$

其中，$X \setminus Y$ 表示集合的相对补集。Tversky 系数可以理解为 Jaccard 系数和 Dice 系数的一般化，当 $\alpha = \beta = 1$ 时为 Jaccard 系数，当 $\alpha = \beta = 0.5$ 时为 Dice 系数。

字符串距离 (Distance of Strings)

对于两个字符串之间的相似性度量，主要有如下几种方法：

• Levenshtein 距离

Levenshtein 距离是 编辑距离 (Editor Distance) 的一种，指两个字串之间，由一个转成另一个所需的最少编辑操作次数。允许的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。例如将 kitten 转成 sitting，转换过程如下：

$$ \begin{equation*} \begin{split} \text{kitten} \to \text{sitten} \left(k \to s\right) \\ \text{sitten} \to \text{sittin} \left(e \to i\right) \\ \text{sittin} \to \text{sitting} \left(\ \to g\right) \end{split} \end{equation*} $$

编辑距离的求解可以利用动态规划的思想优化计算的时间复杂度。

• Jaro-Winkler 距离

对于给定的两个字符串 $s_1$ 和 $s_2$，Jaro 相似度定义为：

$$ sim = \begin{cases} 0 & \text{if} \ m = 0 \\ \dfrac{1}{3} \left(\dfrac{m}{\left|s_1\right|} + \dfrac{m}{\left|s_2\right|} + \dfrac{m-t}{m}\right) & \text{otherwise} \end{cases} $$

其中，$\left|s_i\right|$ 为字符串 $s_i$ 的长度，$m$ 为匹配的字符的个数，$t$ 换位数目的一半。如果字符串 $s_1$ 和 $s_2$ 相差不超过 $\lfloor \dfrac{\max \left(\left|s_1\right|, \left|s_2\right|\right)}{2} \rfloor - 1$，我们则认为两个字符串是匹配的。例如，对于字符串 CRATE 和 TRACE，仅 R, A, E 三个字符是匹配的，因此 $m = 3$，尽管 C, T 均出现在两个字符串中，但是他们的距离超过了 1 (即，$\lfloor \dfrac{5}{2} \rfloor - 1$)，因此 $t = 0$。

Jaro-Winkler 相似度给予了起始部分相同的字符串更高的分数，其定义为：

$$ sim_w = sim_j + l p \left(1 - sim_j\right) $$

其中，$sim_j$ 为字符串 $s_1$ 和 $s_2$ 的 Jaro 相似度，$l$ 为共同前缀的长度 (规定不超过 $4$)，$p$ 为调整系数 (规定不超过 $0.25$)，Winkler 将其设置为 $p = 0.1$。

• 汉明距离

汉明距离为两个等长字符串对应位置的不同字符的个数，也就是将一个字符串变换成另外一个字符串所需要替换的字符个数。例如：1011101 与 1001001 之间的汉明距离是 2，“toned” 与 “roses” 之间的汉明距离是 3。

信息论距离 (Information Theory Distance)

首先我们需要理解什么是 熵 (Entropy)？熵最早是用来表示物理学中一个热力系统无序的程度，后来依据香农的信息论，熵用来衡量一个随机变量的不确定性程度。对于一个随机变量 $X$，其概率分布为：

$$ P \left(X = x_i\right) = p_i, \quad i = 1, 2, ..., n $$

则随机变量 $X$ 的熵定义如下：

$$ H \left(X\right) = - \sum_{i=1}^{n} P \left(x_i\right) \log P \left(x_i\right) \label{eq:entropy} $$

例如抛一枚硬币，假设硬币正面向上 $X = 1$ 的概率为 $p$，硬币反面向上 $X = 0$ 的概率为 $1 - p$。则对于抛一枚硬币那个面朝上这个随机变量 $X$ 的熵为：

$$ H \left(X\right) = - p \log p - \left(1-p\right) \log \left(1-p\right) $$

随概率 $p$ 变化如下图所示：

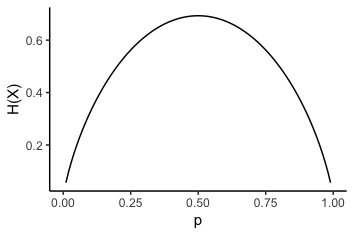
从图可以看出，当 $p = 0.5$ 时熵最大，也就是说抛一枚硬币，当正反两面朝上的概率相同时，熵最大，系统最复杂。对于公式 $\ref{eq:entropy}$，当取以 2 为底的对数时，熵的单位为比特 (bit)，当取自然对数时，熵的单位为纳特 (nat)，当取以 10 为底的对数时，熵的单位为哈特 (hart)。

对于随机变量 $\left(X, Y\right)$，其联合概率分布为：

$$ P \left(X = x_i, Y = y_i\right) = p_{i, j}, \quad i = 1,2,...,n; \quad j = 1,2,...,m $$

条件熵 (Conditional Entropy) 表示在已知 $X$ 的条件下 $Y$ 的不确定性，定义为：

$$ \begin{equation} \begin{split} H \left(Y | X\right) &= \sum_{i=i}^{n} P \left(x_i\right) H \left(Y | X = x_i\right) \\ &= \sum_{i=1}^{n}{\sum_{j=1}^{m}{P \left(x_i, y_j\right) \log \dfrac{P \left(x_i\right)}{P \left(x_i, y_j\right)}}} \end{split} \end{equation} $$

联合熵 (Joint Entropy) 用于衡量多个随机变量的随机系统的信息量，定义为：

$$ H \left(X, Y\right) = \sum_{i=1}^{n}{\sum_{j=1}^{m}{P \left(x_i, y_j\right) \log P \left(x_i, y_j\right)}} $$

• 互信息 (Mutual Information)

互信息用于衡量两个变量之间的关联程度，定义为：

$$ I \left(X; Y\right) = \sum_{i=1}^{n}{\sum_{j=1}^{m}{P \left(x_i, y_j\right) \log \dfrac{P \left(x_i, y_i\right)}{P \left(x_i\right) P \left(y_j\right)}}} $$

直观上，互信息度量 $X$ 和 $Y$ 共享的信息，它度量知道这两个变量其中一个，对另一个不确定度减少的程度。

• 相对熵 (Relative Entropy)

相对熵又称之为 KL 散度 (Kullback-Leibler Divergence)，用于衡量两个分布之间的差异，定义为：

$$ D_{KL} \left(P \| Q\right) = \sum_{i}{P \left(i\right) \ln \dfrac{P \left(i\right)}{Q \left(i\right)}} $$

KL 散度为非负数 $D_{KL} \left(P \| Q\right) \geq 0$，同时其不具有对称性 $D_{KL} \left(P \| Q\right) \neq D_{KL} \left(Q \| P\right)$，也不满足距离函数的三角不等式。

• 交叉熵 (Corss Entropy)

交叉熵定义为：

$$ \begin{equation} \begin{split} H \left(P, Q\right) &= H \left(P\right) + D_{KL} \left(P \| Q\right) \\ &= - \sum_{i}{P \left(i\right) \log Q \left(i\right)} \end{split} \end{equation} $$

交叉熵常作为机器学习中的损失函数，用于衡量模型分布和训练数据分布之间的差异性。

• JS 散度 (Jensen-Shannon Divergence)

JS 散度解决了 KL 散度不对称的问题，定义为：

$$ D_{JS} \left(P \| Q\right) = \dfrac{1}{2} D_{KL} \left(P \| \dfrac{P + Q}{2}\right) + \dfrac{1}{2} D_{KL} \left(Q \| \dfrac{P + Q}{2}\right) $$

当取以 2 为底的对数时，JS 散度的取值范围为：$\left[0, 1\right]$。

• 推土机距离 (Earth Mover Distance, Wasserstein Distance)

推土机距离用于描述两个多维分布之间相似性，之所以称为推土机距离是因为我们将分布看做空间中的泥土，两个分布之间的距离则是通过泥土的搬运将一个分布改变到另一个分布所消耗的最小能量 (即运送距离和运送重量的乘积)。

对于给定的分布 $P = \left\{\left(p_1, w_{p1}\right), \left(p_2, w_{p2}\right), \cdots, \left(p_m, w_{pm}\right)\right\}$ 和 $Q = \left\{\left(q_1, w_{q1}\right), \left(q_2, w_{q2}\right), \cdots, \left(q_n, w_{qn}\right)\right\}$，定义从 $p_i$ 到 $q_j$ 之间的距离为 $d_{i, j}$，所需运送的重量为 $f_{i, j}$。对于 $f_{i, j}$ 有如下 4 个约束：

1. 运送需从 $p_i$ 到 $q_j$，不能反向，即 $f_{i, j} \geq 0, 1 \leq i \leq m, 1 \leq j \leq n$。
2. 从 $p_i$ 运送出的总重量不超过原始的总重量 $w_{pi}$，即 $\sum_{j=1}^{n}{f_{i, j}} \leq w_{pi}, 1 \leq i \leq m$。
3. 运送到 $q_j$ 的总重量不超过其总容量 $w_{qj}$，即 $\sum_{i=1}^{m}{f_{i, j}} \leq w_{qj}, 1 \leq j \leq n$。
4. $\sum_{i=1}^{m}{\sum_{j=1}^{n}{f_{i, j}}} = \min \left\{\sum_{i=1}^{m}{w_{pi}}, \sum_{j=1}^{n}{w_{qj}}\right\}$。

在此约束下，通过最小化损失函数：

$$ \min \sum_{i=1}^{m}{\sum_{j=1}^{n}{d_{i, j} f_{i, j}}} $$

得到最优解 $f_{i, j}^*$，则推土机距离定义为：

$$ D_{W} \left(P, Q\right) = \dfrac{\sum_{i=1}^{m}{\sum_{j=1}^{n}{d_{i, j} f_{i, j}^*}}}{\sum_{i=1}^{m}{\sum_{j=1}^{n}{f_{i, j}^*}}} $$

其他距离 (Other Distance)

• DTW (Dynamic Time Warping) 距离

DTW 距离用于衡量两个序列之间的相似性，序列的长度可能相等也可能不相等。对于两个给定的序列 $X = \left(x_1, x_2, \cdots, x_m\right)$ 和 $Y = \left(y_1, y_2, \cdots, y_n\right)$，我们可以利用动态规划的方法求解 DTW 距离。首先我们构造一个 $m \times n$ 的矩阵，矩阵中的元素 $d_{i, j}$ 表示 $x_i$ 和 $y_j$ 之间的距离。我们需要找到一条通过该矩阵的路径 $W = \left(w_1, w_2, \cdots, w_l\right)$, $\max\left(m, n\right) \leq l < m + n + 1$，假设 $w_k$ 对应的矩阵元素为 $\left(i, j\right)$，对应的距离为 $d_k$，则 DTW 的优化目标为 $\min \sum_{k=1}^{l}{d_k}$。如下图右上角部分所示：

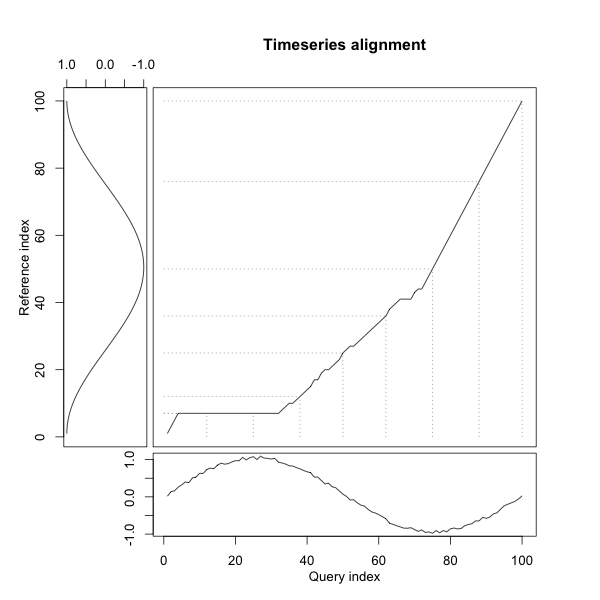
对于路径 $W$，需要满足如下 3 个条件：

1. 边界条件：$w_1 = \left(1, 1\right), w_k = \left(m, n\right)$，即路径须从左下角出发，在右上角终止。
2. 连续性：对于 $w_{l-1} = \left(i', j'\right), w_l = \left(i, j\right)$，需满足 $i - i' \leq 1, j - j' \leq 1$，即路径不能跨过任何一点进行匹配。
3. 单调性：对于 $w_{l-1} = \left(i', j'\right), w_l = \left(i, j\right)$，需满足 $0 \leq i - i', 0 \leq j - j'$，即路径上的点需单调递增，不能回退进行匹配。

利用动态规划求解 DTW 的状态转移方程为：

$$ dtw_{i, j} = \begin{cases} 0 & \text{if} \ i = j = 0 \\ \infty & \text{if} \ i = 0 \ \text{or} \ j = 0 \\ d_{i, j} + \min \left(dtw_{i-1, j}, dtw_{i-1, j-1}, dtw_{i, j-1}\right) & \text{otherwise} \end{cases} $$

$dtw_{m, n}$ 则为最终的 DTW 距离。在 DTW 求解的过程中还可以使用不同的 Local Warping Step 和窗口类型，更多详细信息可看见 R 中 dtw 包。下图展示了利用 DTW 求解后不同点之间的对应关系：

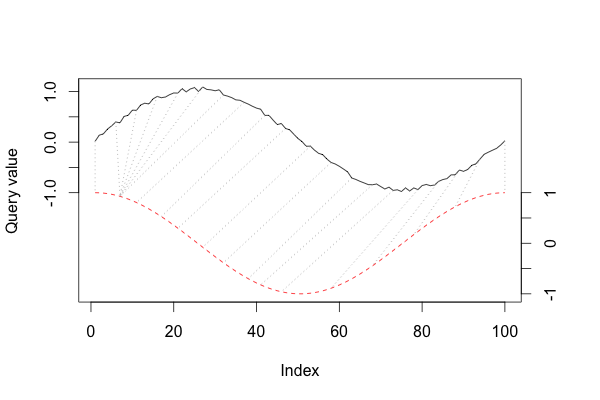
• 流形距离 (Distance of Manifold)

关于流形距离请参见之前的博客：流形学习 (Manifold Learning)。

:tada::tada::tada: Happe New Year! :tada::tada::tada:

「真诚赞赏，手留余香」

￥ 2 ￥ 5 ￥ 10 ￥ 50 ￥ 100 任意金额