多臂赌博机 (Multi-armed Bandit)
强化学习系列
范叶亮 / 2020-05-16
分类: 机器学习, 强化学习 / 标签: 强化学习, Reinforcement Learning, 多臂赌博机, Multi-armed Bandit, Epsilon Greedy, Upper Confidence Bound, UCB, Gradient Bandit / 字数: 2784
多臂赌博机问题
一个赌徒，要去摇老虎机，走进赌场一看，一排老虎机，外表一模一样，但是每个老虎机吐钱的概率可不一样，他不知道每个老虎机吐钱的概率分布是什么，那么每次该选择哪个老虎机可以做到最大化收益呢？这就是多臂赌博机问题 (Multi-armed bandit problem, K- or N-armed bandit problem, MAB) 2。
$k$ 臂赌博机问题中，$k$ 个动作的每一个在被选择时都有一个期望或者平均收益，称之为这个动作的**“价值”**。令 $t$ 时刻选择的动作为 $A_t$，对应的收益为 $R_t$，任一动作 $a$ 对应的价值为 $q_* \left(a\right)$，即给定动作 $a$ 时收益的期望：
$$ q_* \left(a\right) = \mathbb{E} \left[R_t | A_t = a\right] $$
我们将对动作 $a$ 在时刻 $t$ 的价值的估计记做 $Q_t \left(a\right)$，我们希望它接近 $q_* \left(a\right)$。
如果持续对动作的价值进行估计，那么在任一时刻都会至少有一个动作的估计价值是最高的，将这些对应最高估计价值的动作成为贪心的动作。当从这些动作中选择时，称此为开发当前所知道的关于动作的价值的知识。如果不是如此，而是选择非贪心的动作，称此为试探，因为这可以让你改善对非贪心动作的价值的估计。“开发”对于最大化当前这一时刻的期望收益是正确的做法，但是“试探”从长远来看可能会带来总体收益的最大化。到底选择“试探”还是“开发”一种复杂的方式依赖于我们得到的函数估计、不确定性和剩余时刻的精确数值。
动作价值估计方法
我们以一种自然的方式，就是通过计算实际收益的平均值来估计动作的价值：
$$ \begin{aligned} Q_t \left(a\right) &= \dfrac{t \text{ 时刻前执行动作 } a \text{ 得到的收益总和 }}{t \text{ 时刻前执行动作 } a \text{ 的次数}} \\ &= \dfrac{\sum_{i=1}^{t-1}{R_i \cdot \mathbb{1}_{A_i = a}}}{\sum_{i=1}^{t-1}{\mathbb{1}_{A_i = a}}} \end{aligned} $$
其中，$\mathbb{1}_{\text{predicate}}$ 表示随机变量，当 predicate 为真时其值为 1，反之为 0。当分母为 0 时，$Q_t \left(a\right) = 0$，当分母趋向无穷大时，根据大数定律，$Q_t \left(a\right)$ 会收敛到 $q_* \left(a\right)$。这种估计动作价值的方法称为采样平均方法，因为每一次估计都是对相关收益样本的平均。
当然，这只是估计动作价值的一种方法，而且不一定是最好的方法。例如，我们也可以利用累积遗憾（Regret）来评估动作的价值：
$$ \rho = T \mu^* - \sum_{t=1}^{T} \hat{r}_t $$
其中，$\mu^* = \mathop{\max}_{k} \left\{\mu_k\right\}$ 为最大的回报，$\hat{r}_t$ 为 $t$ 时刻的回报。
多臂赌博机算法
以 10 臂赌博机为例，动作的收益分布如下图所示：
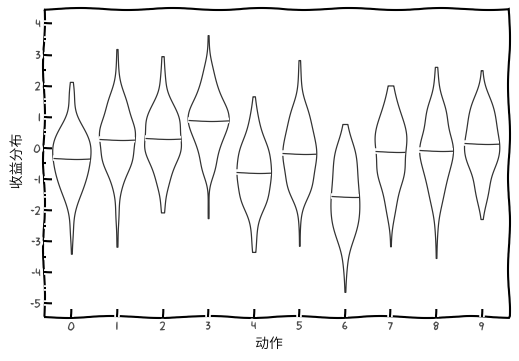
动作的真实价值 $q_* \left(a\right), a = 1, \cdots, 10$ 为从一个均值为 0 方差为 1 的标准正态分布中选择。当对于该问题的学习方法在 $t$ 时刻选择 $A_t$ 时，实际的收益 $R_t$ 则由一个均值为 $q_* \left(A_t\right)$ 方差为 1 的正态分布决定。
$\epsilon$-Greedy
$\epsilon$-Greedy 采用的动作选择逻辑如下：
- 确定一个
$\epsilon \in \left(0, 1\right)$。 - 每次以
$\epsilon$的概率随机选择一个臂，以$1 - \epsilon$选择平均收益最大的那个臂。
下图分别展示了 $\epsilon = 0$（贪婪），$\epsilon = 0.01$ 和 $\epsilon = 0.1$ 三种情况下的平均收益和最优动作占比随训练步数的变化情况。
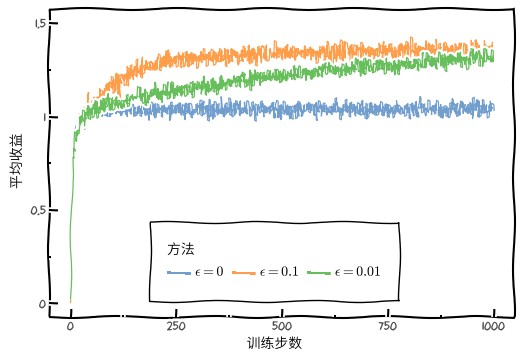
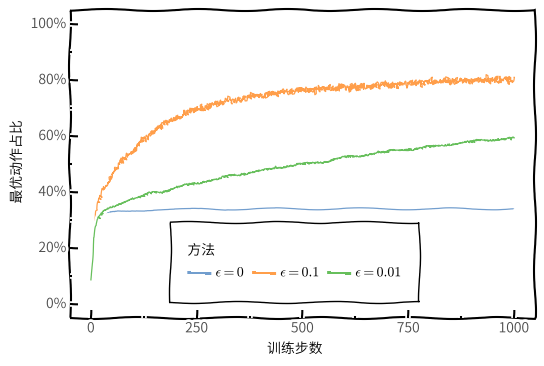
$\epsilon$-Greedy 相比于 $\epsilon = 0$（贪婪）算法的优势如下：
- 对于更大方差的收益，找到最优的动作需要更多次的试探。
- 对于非平稳的任务，即动作的真实价值会随着时间而改变，这种情况下即使有确定性的情况下，也需要进行试探。
令 $R_i$ 表示一个动作被选择 $i$ 次后获得的收益，$Q_n$ 表示被选择 $n - 1$ 次后它的估计的动作价值，其可以表示为增量计算的形式：
$$ \begin{aligned} Q_{n+1} &= \dfrac{1}{n} \sum_{i=1}^{n}{R_i} \\ &= \dfrac{1}{n} \left(R_n + \sum_{i=1}^{n-1}{R_i}\right) \\ &= \dfrac{1}{n} \left(R_n + \left(n - 1\right) \dfrac{1}{n-1} \sum_{i=1}^{n-1}{R_i}\right) \\ &= \dfrac{1}{n} \left(R_n + \left(n - 1\right) Q_n\right) \\ &= \dfrac{1}{n} \left(R_n + n Q_n - Q_n\right) \\ &= Q_n + \dfrac{1}{n} \left[R_n - Q_n\right] \end{aligned} $$
上述我们讨论的都是平稳的问题，即收益的概率分布不随着时间变化的赌博机问题。对于非平稳的问题，给近期的收益赋予比过去更高的权值是一个合理的处理方式。则收益均值 $Q_n$ 的增量更新规则为：
$$ \begin{aligned} Q_{n+1} &= Q_n + \alpha \left[R_n - Q_n\right] \\ &= \left(1 - \alpha\right)^n Q_1 + \sum_{i=1}^{n} \alpha \left(1 - \alpha\right)^{n-i} R_i \end{aligned} $$
赋给收益 $R_i$ 的权值 $\alpha \left(1 - \alpha\right)^{n-i}$ 依赖于它被观测到的具体时刻和当前时刻的差，权值以指数形式递减，因此这个方法也称之为指数近因加权平均。
上述讨论中所有方法都在一定程度上依赖于初始动作值 $Q_1 \left(a\right)$ 的选择。从统计学角度，初始估计值是有偏的，对于平均采样来说，当所有动作都至少被选择一次时，偏差会消失；对于步长为常数的情况，偏差会随时间而减小。
下图展示了不同初始动作估计值下最优动作占比随训练步数的变化情况：
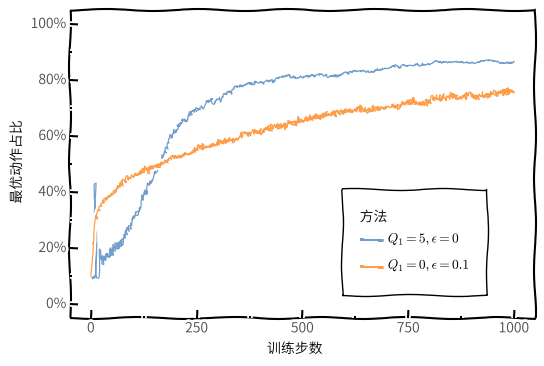
设置较大初始动作估计值会鼓励进行试探，这种方法称之为乐观初始价值，该方法在平稳问题中非常有效。
UCB
$\epsilon$-Greedy 在进行尝试时是盲目地选择，因为它不大会选择接近贪心或者不确定性特别大的动作。在非贪心动作中，最好是根据它们的潜力来选择可能事实上是最优的动作，这要考虑它们的估计有多接近最大值，以及这些估计的不确定性。
一种基于置信度上界（Upper Confidence Bound，UCB）思想的选择动作依据如下：
$$ A_t = \mathop{\arg\max}_{a} \left[Q_t \left(a\right) + c \sqrt{\dfrac{\ln t}{N_t \left(a\right)}}\right] $$
其中，$N_t \left(a\right)$ 表示在时刻 $t$ 之前动作 $a$ 被选择的次数，$c > 0$ 用于控制试探的程度。平方根项是对 $a$ 动作值估计的不确定性或方差的度量，最大值的大小是动作 $a$ 的可能真实值的上限，参数 $c$ 决定了置信水平。
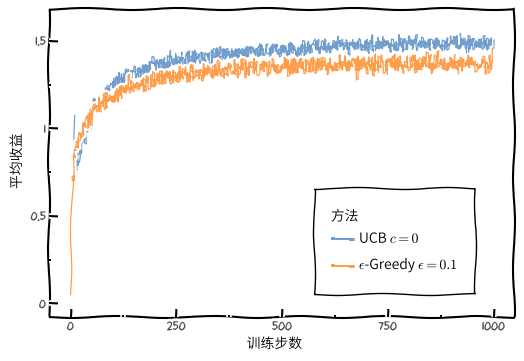
下图展示了 UCB 算法和 $\epsilon$-Greedy 算法平均收益随着训练步数的变化：
梯度赌博机算法
针对每个动作 $a$，考虑学习一个数值化的偏好函数 $H_t \left(a\right)$，偏好函数越大，动作就约频繁地被选择，但偏好函数的概念并不是从“收益”的意义上提出的。基于随机梯度上升的思想，在每个步骤中，在选择动作 $A_t$ 并获得收益 $R_t$ 之后，偏好函数会按如下方式更新：
$$ \begin{aligned} H_{t+1} \left(A_t\right) &eq H_t \left(A_t\right) + \alpha \left(R_t - \bar{R}_t\right) \left(1 - \pi_t \left(A_t\right)\right) \\ H_{t+1} \left(a\right) &eq H_t \left(a\right) - \alpha \left(R_t - \bar{R}_t\right) \pi_t \left(a\right) \end{aligned} $$
其中，$\alpha > 0$ 表示步长，$\bar{R}_t \in \mathbb{R}$ 表示时刻 $t$ 内所有收益的平均值。$\bar{R}_t$ 项作为比较收益的一个基准项，如果收益高于它，那么在未来选择动作 $A_t$ 的概率就会增加，反之概率就会降低，未选择的动作被选择的概率会上升。
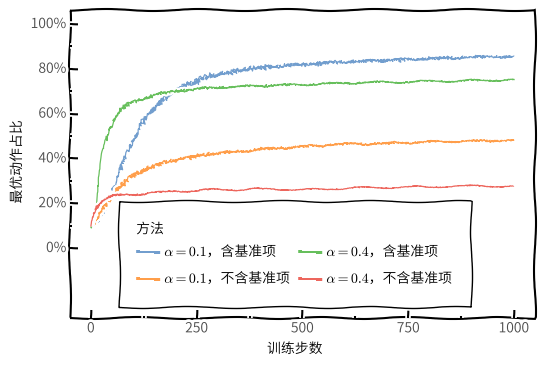
下图展示了在 10 臂测试平台问题的变体上采用梯度赌博机算法的结果，在这个问题中，它们真实的期望收益是按照平均值为 4 而不是 0 的正态分布来选择的。所有收益的这种变化对梯度赌博机算法没有任何影响，因为收益基准项让它可以马上适应新的收益水平，如果没有基准项，那么性能将显著降低。
算法性能比较
$\epsilon$-Greedy 方法在一段时间内进行随机的动作选择；UCB 方法虽然采用确定的动作选择，但可以通过每个时刻对具有较少样本的动作进行优先选择来实现试探；梯度赌博机算法则不估计动作价值，而是利用偏好函数，使用 softmax 分布来以一种分级的、概率式的方式选择更优的动作；简单地将收益的初值进行乐观的设置，可以让贪心方法也能进行显示试探。
下图展示了上述算法在不同参数下的平均收益，每条算法性能曲线都看作一个自己参数的函数。$x$ 轴上参数值的变化是 2 的倍数，并以对数坐标轴进行表示。
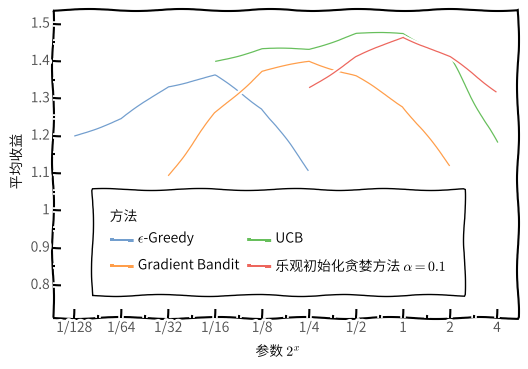
在评估方法时，不仅要关注它在最佳参数设置上的表现，还要注意它对参数值的敏感性。总的来说，在本文的问题上，UCB 表现最好。
-
Sutton, R. S., & Barto, A. G. (2018). Reinforcement learning: An introduction. MIT press. ↩︎