马尔可夫决策过程 (Markov Decision Process)

强化学习系列

范叶亮 / 2020-05-23

分类: 机器学习, 强化学习 / 标签: 强化学习, Reinforcement Learning, 马尔可夫模型, Markov Model, 马尔可夫链, Markov Chain, MC, 隐马尔可夫模型, Hidden Markov Model, HMM, 马尔可夫奖励过程, Markov Reward Process, MRP, 分幕, 马尔可夫决策过程, Markov Decision Process, MDP, 部分可观测马尔可夫决策过程, Partially Observable Markov Decision Process, POMDP / 字数: 2928

本文为《强化学习系列》文章
本文内容主要参考自：
1.《强化学习》¹
2. CS234: Reinforcement Learning ²
3. UCL Course on RL ³

马尔可夫模型

马尔可夫模型是一种用于序列数据建模的随机模型，其假设未来的状态仅取决于当前的状态，即：

$$ \mathbb{P} \left[S_{t+1} | S_t\right] = \mathbb{P} \left[S_{t+1} | S_1, \cdots, S_t\right] $$

也就是认为当前状态捕获了历史中所有相关的信息。根据系统状态是否完全可被观测以及系统是自动的还是受控的，可以将马尔可夫模型分为 4 种，如下表所示：

	状态状态完全可被观测	系统状态不是完全可被观测
状态是自动的	马尔可夫链（MC）	隐马尔可夫模型（HMM）
系统是受控的	马尔可夫决策过程（MDP）	部分可观测马尔可夫决策过程（POMDP）

马尔可夫链（Markov Chain，MC）为从一个状态到另一个状态转换的随机过程，当马尔可夫链的状态只能部分被观测到时，即为隐马尔可夫模型（Hidden Markov Model，HMM），也就是说观测值与系统状态有关，但通常不足以精确地确定状态。马尔可夫决策过程（Markov Decision Process，MDP）也是马尔可夫链，但其状态转移取决于当前状态和采取的动作，通常一个马尔可夫决策过程用于计算依据期望回报最大化某些效用的行动策略。部分可观测马尔可夫决策过程（Partially Observable Markov Decision Process，POMDP）即为系统状态仅部分可见情况下的马尔可夫决策过程。

马尔可夫过程

对于一个马尔可夫状态 $s$ 和一个后继状态 $s'$ ，状态转移概率定义为：

$$ \mathcal{P}_{ss'} = \mathbb{P} \left[S_t = s' | S_{t-1} = s\right] $$

状态概率矩阵 $\mathcal{P}$ 定义了从所有状态 $s$ 到后继状态 $s'$ 的转移概率：

$$ \mathcal{P} = \left[\begin{array}{ccc} \mathcal{P}_{11} & \cdots & \mathcal{P}_{1 n} \\ \vdots & & \\ \mathcal{P}_{n 1} & \cdots & \mathcal{P}_{n n} \end{array}\right] $$

其中每一行的加和为 1。

马尔可夫过程（马尔可夫链）是一个无记忆的随机过程，一个马尔可夫过程可以定义为 $\langle \mathcal{S}, \mathcal{P} \rangle$ ，其中 $\mathcal{S}$ 是一个有限状态集合， $\mathcal{P}_{ss'} = \mathbb{P} \left[S_t = s' | S_{t-1} = s\right]$ ， $\mathcal{P}$ 为状态转移概率矩阵。以一个学生的日常生活为例，Class $i$ 表示第 $i$ 门课程，Facebook 表示在 Facebook 上进行社交，Pub 表示去酒吧，Pass 表示通过考试，Sleep 表示睡觉，这个马尔可夫过程如下图所示：

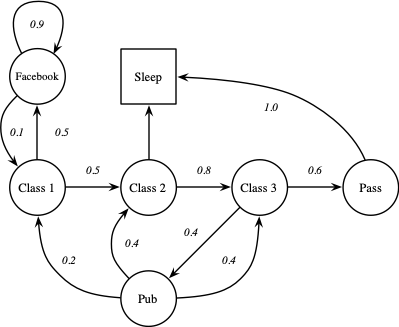
从而可以产生多种不同的序列，例如：

C1 -> C2 -> C3 -> Pass -> Sleep
C1 -> FB -> FB -> C1 -> C2 -> Sleep
C1 -> C2 -> C3 -> Pub -> C2 -> C3 -> Pass -> Sleep

状态转移概率矩阵如下所示：

据此我们可以定义马尔可夫奖励过程（Markov Reward Process，MRP）为 $\langle \mathcal{S, P, R}, \gamma \rangle$ ，其中 $\mathcal{S}$ 和 $\mathcal{P}$ 同马尔可夫过程定义中的参数相同， $\mathcal{R}$ 为收益函数， $\mathcal{R}_s = \mathbb{E} \left[R_t | S_{t-1} = s\right]$ ， $\gamma \in \left[0, 1\right]$ 为折扣率。如下图所示：

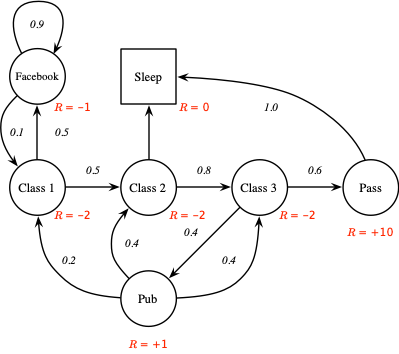
期望回报 $G_t$ 定义为从时刻 $t$ 之后的所有衰减的收益之和，即：

$$ G_t = R_{t+1} + \gamma R_{t+2} + \cdots = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1} $$

当 $\gamma$ 接近 $0$ 时，智能体更倾向于近期收益，当 $\gamma$ 接近 $1$ 时，智能体更侧重考虑长远收益。邻接时刻的收益可以按如下递归方式表示：

$$ G_t = R_{t+1} + \gamma G_{t+1} $$

对于存在“最终时刻”的应用中，智能体和环境的交互能被自然地分成一个系列子序列，每个子序列称之为“幕（episodes）”，例如一盘游戏、一次走迷宫的过程，每幕都以一种特殊状态结束，称之为终结状态。这些幕可以被认为在同样的终结状态下结束，只是对不同的结果有不同的收益，具有这种分幕重复特性的任务称之为分幕式任务。

MRP 的状态价值函数 $v \left(s\right)$ 给出了状态 $s$ 的长期价值，定义为：

$$ \begin{aligned} v(s) &=\mathbb{E}\left[G_{t} | S_{t}=s\right] \\ &=\mathbb{E}\left[R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\ldots | S_{t}=s\right] \\ &=\mathbb{E}\left[R_{t+1}+\gamma\left(R_{t+2}+\gamma R_{t+3}+\ldots\right) | S_{t}=s\right] \\ &=\mathbb{E}\left[R_{t+1}+\gamma G_{t+1} | S_{t}=s\right] \\ &=\mathbb{E}\left[R_{t+1}+\gamma v\left(S_{t+1}\right) | S_{t}=s\right] \end{aligned} $$

价值函数可以分解为两部分：即时收益 $R_{t+1}$ 和后继状态的折扣价值 $\gamma v \left(S_{t+1}\right)$ 。上式我们称之为贝尔曼方程（Bellman Equation），其衡量了状态价值和后继状态价值之间的关系。

马尔可夫决策过程

一个马尔可夫决策过程（Markov Decision Process，MDP）定义为包含决策的马尔可夫奖励过程 $\langle\mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma\rangle$ ，在这个环境中所有的状态均具有马尔可夫性。其中， $\mathcal{S}$ 为有限的状态集合， $\mathcal{A}$ 为有限的动作集合， $\mathcal{P}$ 为状态转移概率矩阵， $\mathcal{P}_{s s^{\prime}}^{a}=\mathbb{P}\left[S_{t+1}=s^{\prime} | S_{t}=s, A_{t}=a\right]$ ， $\mathcal{R}$ 为奖励函数， $\mathcal{R}_{s}^{a}=\mathbb{E}\left[R_{t+1} | S_{t}=s, A_{t}=a\right]$ ， $\gamma \in \left[0, 1\right]$ 为折扣率。上例中的马尔可夫决策过程如下图所示：

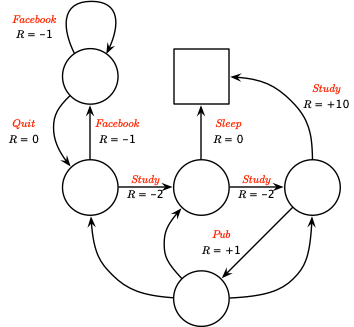
策略（Policy）定义为给定状态下动作的概率分布：

$$ \pi \left(a | s\right) = \mathbb{P} \left[A_t = a | S_t = s\right] $$

一个策略完全确定了一个智能体的行为，同时 MDP 策略仅依赖于当前状态。给定一个 MDP $\mathcal{M}=\langle\mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma\rangle$ 和一个策略 $\pi$ ，状态序列 $S_1, S_2, \cdots$ 为一个马尔可夫过程 $\langle \mathcal{S}, \mathcal{P}^{\pi} \rangle$ ，状态和奖励序列 $S_1, R_2, S_2, \cdots$ 为一个马尔可夫奖励过程 $\left\langle\mathcal{S}, \mathcal{P}^{\pi}, \mathcal{R}^{\pi}, \gamma\right\rangle$ ，其中

$$ \begin{aligned} \mathcal{P}_{s s^{\prime}}^{\pi} &=\sum_{a \in \mathcal{A}} \pi(a | s) \mathcal{P}_{s s^{\prime}}^{a} \\ \mathcal{R}_{s}^{\pi} &=\sum_{a \in \mathcal{A}} \pi(a | s) \mathcal{R}_{s}^{a} \end{aligned} $$

在策略 $\pi$ 下，状态 $s$ 的价值函数记为 $v_{\pi} \left(s\right)$ ，即从状态 $s$ 开始，智能体按照策略进行决策所获得的回报的概率期望值，对于 MDP 其定义为：

$$ \begin{aligned} v_{\pi} \left(s\right) &= \mathbb{E}_{\pi} \left[G_t | S_t = s\right] \\ &= \mathbb{E}_{\pi} \left[\sum_{k=0}^{\infty} \gamma^k R_{t+k+1} | S_t = s\right] \end{aligned} $$

在策略 $\pi$ 下，在状态 $s$ 时采取动作 $a$ 的价值记为 $q_\pi \left(s, a\right)$ ，即根据策略 $\pi$ ，从状态 $s$ 开始，执行动作 $a$ 之后，所有可能的决策序列的期望回报：

$$ \begin{aligned} q_\pi \left(s, a\right) &= \mathbb{E}_{\pi} \left[G_t | S_t = s, A_t = a\right] \\ &= \mathbb{E}_{\pi} \left[\sum_{k=0}^{\infty} \gamma^k R_{t+k+1} | S_t = s, A_t = a\right] \end{aligned} $$

状态价值函数 $v_{\pi}$ 和动作价值函数 $q_{\pi}$ 都能从经验中估计得到，两者都可以分解为当前和后继两个部分：

$$ \begin{aligned} v_{\pi}(s) &= \mathbb{E}_{\pi}\left[R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) | S_{t}=s\right] \\ q_{\pi}(s, a) &= \mathbb{E}_{\pi}\left[R_{t+1}+\gamma q_{\pi}\left(S_{t+1}, A_{t+1}\right) | S_{t}=s, A_{t}=a\right] \end{aligned} $$

从一个状态 $s$ 出发，采取一个行动 $a$ ，状态价值函数为：

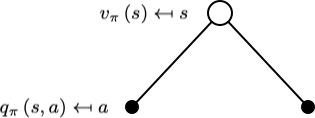
$$ v_{\pi}(s)=\sum_{a \in \mathcal{A}} \pi(a | s) q_{\pi}(s, a) $$

从一个动作 $s$ 出发，再采取一个行动 $a$ 后，动作价值函数为：

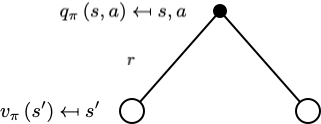
$$ q_{\pi}(s, a)=\mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}}^{a} v_{\pi}\left(s^{\prime}\right) $$

利用后继状态价值函数表示当前状态价值函数为：

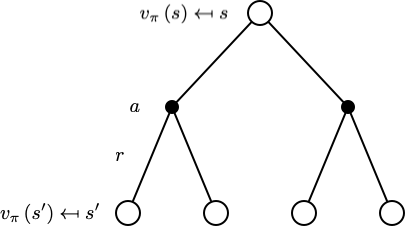
$$ v_{\pi}(s)=\sum_{a \in \mathcal{A}} \pi(a | s)\left(\mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}}^{a} v_{\pi}\left(s^{\prime}\right)\right) $$

利用后继动作价值函数表示当前动作价值函数为：

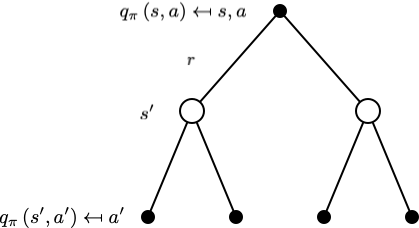
$$ q_{\pi}(s, a)=\mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}}^{a} \sum_{a^{\prime} \in \mathcal{A}} \pi\left(a^{\prime} | s^{\prime}\right) q_{\pi}\left(s^{\prime}, a^{\prime}\right) $$

最优状态价值函数 $v_* \left(s\right)$ 定义为所有策略上最大值的状态价值函数：

$$ v_* \left(s\right) = \mathop{\max}_{\pi} v_{\pi} \left(s\right) $$

最优动作价值函数 $q_* \left(s, a\right)$ 定义为所有策略上最大值的动作价值函数：

$$ q_* \left(s, a\right) = \mathop{\max}_{\pi} q_{\pi} \left(s, a\right) $$

定义不同策略之间的大小关系为：

$$ \pi \geq \pi^{\prime} \text { if } v_{\pi}(s) \geq v_{\pi^{\prime}}(s), \forall s $$

对于任意一个马尔可夫决策过程有：

存在一个比其他策略更优或相等的策略， $\pi_* \geq \pi, \forall \pi$
所有的最优策略均能够获得最优的状态价值函数， $v_{\pi_*} \left(s\right) = v_* \left(s\right)$
所有的最优策略均能够获得最优的动作价值函数， $q_{\pi_*} \left(s, a\right) = q_* \left(s, a\right)$

一个最优策略可以通过最大化 $q_* \left(s, a\right)$ 获得：

$$ \pi_{*}(a | s)=\left\{\begin{array}{ll} 1 & \text { if } a=\underset{a \in \mathcal{A}}{\operatorname{argmax}} q_{*}(s, a) \\ 0 & \text { otherwise } \end{array}\right. $$

对于任意一个 MDP 均会有一个确定的最优策略，如果已知 $q_* \left(s, a\right)$ 即可知晓最优策略。

最优状态价值函数循环依赖于贝尔曼最优方程：

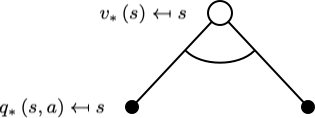
$$ v_{*}(s)=\max _{a} q_{*}(s, a) $$

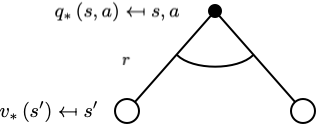
$$ q_{*}(s, a)=\mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}}^{a} v_{*}\left(s^{\prime}\right) $$

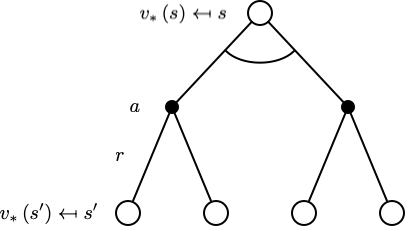
$$ v_{*}(s)=\max _{a} \mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}}^{a} v_{*}\left(s^{\prime}\right) $$

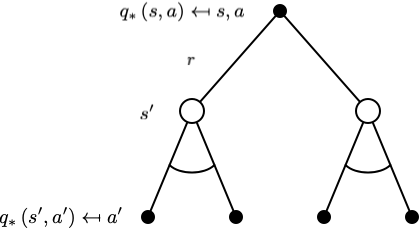
$$ q_{*}(s, a)=\mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}}^{a} \max _{a^{\prime}} q_{*}\left(s^{\prime}, a^{\prime}\right) $$

显式求解贝尔曼最优方程给出了找到一个最优策略的方法，但这种解法至少依赖于三条实际情况很难满足的假设：

准确地知道环境的动态变化特性
有足够的计算资源来求解
马尔可夫性质

尤其是假设 2 很难满足，现实问题中状态的数量一般很大，即使利用最快的计算机也需要花费难以接受的时间才能求解完成。

Sutton, R. S., & Barto, A. G. (2018). Reinforcement learning: An introduction. MIT press. ↩︎
CS234: Reinforcement Learning http://web.stanford.edu/class/cs234/index.html ↩︎
UCL Course on RL https://www.davidsilver.uk/teaching ↩︎

markov-decision-process