本文为《强化学习系列》文章
本文内容主要参考自：
1.《强化学习》¹
2. CS234: Reinforcement Learning ²
3. UCL Course on RL ³

动态规划

动态规划（Dynamic Programming，DP）是一种用于解决具有如下两个特性问题的通用算法：

1. 优化问题可以分解为子问题。
2. 子问题出现多次并可以被缓存和复用。

马尔可夫决策过程正符合这两个特性：

1. 贝尔曼方程给定了迭代过程的分解。
2. 价值函数保存并复用了解决方案。

在强化学习中，DP 的核心思想是使用价值函数来结构化地组织对最优策略的搜索。一旦得到了满足贝尔曼最优方程的价值函数 $v_*$ 或 $q_*$，得到最优策略就容易了。对于任意 $s \in \mathcal{S}$（状态集合），$a \in \mathcal{A} \left(s\right)$（动作集合）和 $s' \in \mathcal{S}^{+}$（在分幕式任务下 $\mathcal{S}$ 加上一个终止状态），有：

$$ \begin{aligned} v_{*}(s) &=\max _{a} \mathbb{E}\left[R_{t+1}+\gamma v_{*}\left(S_{t+1}\right) | S_{t}=s, A_{t}=a\right] \\ &=\max _{a} \sum_{s^{\prime}, r} p\left(s^{\prime}, r | s, a\right)\left[r+\gamma v_{*}\left(s^{\prime}\right)\right] \end{aligned} $$

$$ \begin{aligned} q_{*}(s, a) &=\mathbb{E}\left[R_{t+1}+\gamma \max _{a^{\prime}} q_{*}\left(S_{t+1}, a^{\prime}\right) | S_{t}=s, A_{t}=a\right] \\ &\left.=\sum_{s^{\prime}, r} p\left(s^{\prime}, r | s, a\right)\left[r+\gamma \max _{a^{\prime}}\right] q_{*}\left(s^{\prime}, a^{\prime}\right)\right] \end{aligned} $$

将贝尔曼方程转化成为近似逼近理想价值函数的递归更新公式，我们就得到了 DP 算法。

策略评估

对于一个策略 $\pi$，如何计算其状态价值函数 $v_{\pi}$ 被称为策略评估。对于任意 $s \in \mathcal{S}$，有：

$$ \begin{aligned} v_{\pi}(s) & \doteq \mathbb{E}_{\pi}\left[G_{t} | S_{t}=s\right] \\ &=\mathbb{E}_{\pi}\left[R_{t+1}+\gamma G_{t+1} | S_{t}=s\right] \\ &=\mathbb{E}_{\pi}\left[R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) | S_{t}=s\right] \\ &=\sum_{a} \pi(a | s) \sum_{s^{\prime}, r} p\left(s^{\prime}, r | s, a\right)\left[r+\gamma v_{\pi}\left(s^{\prime}\right)\right] \end{aligned} $$

其中 $\pi \left(a | s\right)$ 表示在环境 $s$ 中智能体在策略 $\pi$ 下采取动作 $a$ 的概率。只要 $\gamma < 1$ 或者任何状态在 $\pi$ 下都能保证最后终止，则 $v_{\pi}$ 唯一存在。

考虑一个近似的价值函数序列 $v_0, v_1, \cdots$，从 $\mathcal{S}^{+}$ 映射到 $\mathbb{R}$，初始的近似值 $v_0$ 可以任意选取（除了终止状态必须为 0 外）。下一轮迭代的近似可以使用 $v_{\pi}$ 的贝尔曼方程进行更新，对于任意 $s \in \mathcal{S}$ 有：

$$ \begin{aligned} v_{k+1}(s) & \doteq \mathbb{E}_{\pi}\left[R_{t+1}+\gamma v_{k}\left(S_{t+1}\right) | S_{t}=s\right] \\ &=\sum_{a} \pi(a | s) \sum_{s^{\prime}, r} p\left(s^{\prime}, r | s, a\right)\left[r+\gamma v_{k}\left(s^{\prime}\right)\right] \end{aligned} $$

显然，$v_k = v_{\pi}$ 是这个更新规则的一个不动点。在保证 $v_{\pi}$ 存在的条件下，序列 $\left\{v_k\right\}$ 在 $k \to \infty$ 时将会收敛到 $v_{\pi}$，这个算法称作 迭代策略评估。

策略改进

对于任意一个确定的策略 $\pi$，我们已经确定了它的价值函数 $v_{\pi}$。对于某个状态 $s$，我们想知道是否应该选择一个不同于给定的策略的动作 $a \neq \pi \left(s\right)$。如果从状态 $s$ 继续使用现有策略，则最后的结果就是 $v \left(s\right)$，但我们并不知道换成一个新策略后是得到更好的结果还是更坏的结果。一种解决方法是在状态 $s$ 选择动作 $a$ 后，继续遵循现有的策略 $\pi$，则这种方法的价值为：

$$ \begin{aligned} q_{\pi}(s, a) & \doteq \mathbb{E}\left[R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) | S_{t}=s, A_{t}=a\right] \\ &=\sum_{s^{\prime}, r} p\left(s^{\prime}, r | s, a\right)\left[r+\gamma v_{\pi}\left(s^{\prime}\right)\right] \end{aligned} $$

一个关键的准则就是这个值是大于还是小于 $v_{\pi} \left(s\right)$。如果这个值更大，则说明在状态 $s$ 选择动作 $a$，然后继续使用策略 $\pi$ 会比使用始终使用策略 $\pi$ 更优。

上述情况是策略改进定理的一个特例，一般来说，如果 $\pi$ 和 $\pi'$ 是任意两个确定的策略，对于任意 $s \in \mathcal{S}$：

$$ q_{\pi}\left(s, \pi^{\prime}(s)\right) \geq v_{\pi}(s) $$

则称策略 $\pi'$ 相比于 $\pi$ 一样好或更好。也就是说，对于任意状态 $s \in \mathcal{S}$，这样肯定能得到一样或更好的期望回报：

$$ v_{\pi^{\prime}}(s) \geq v_{\pi}(s) $$

延伸到所有状态和所有可能的动作，即在每个状态下根据 $q_{\pi} \left(s, a\right)$ 选择一个最优的，换言之，考虑一个新的贪心策略 $\pi'$，满足：

$$ \begin{aligned} \pi^{\prime}(s) & \doteq \underset{a}{\arg \max } q_{\pi}(s, a) \\ &=\underset{a}{\arg \max } \mathbb{E}\left[R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) | S_{t}=s, A_{t}=a\right] \\ &=\underset{a}{\arg \max } \sum_{s^{\prime}, r} p\left(s^{\prime}, r | s, a\right)\left[r+\gamma v_{\pi}\left(s^{\prime}\right)\right] \end{aligned} $$

这样构造出的贪心策略满足策略改进定理的条件，所以它和原策略相比一样好或更好。这种根据原策略的价值函数执行贪心算法，来构造一个更好策略的过程称之为策略改进。如果新的贪心策略 $\pi'$ 和原策略 $\pi$ 一样好而不是更好，则有 $v_{\pi} = v_{\pi'}$，对任意 $s \in \mathcal{S}$：

$$ \begin{aligned} v_{\pi^{\prime}}(s) &=\max _{a} \mathbb{E}\left[R_{t+1}+\gamma v_{\pi^{\prime}}\left(S_{t+1}\right) | S_{t}=s, A_{t}=a\right] \\ &=\max _{a} \sum_{s^{\prime}, r} p\left(s^{\prime}, r | s, a\right)\left[r+\gamma v_{\pi^{\prime}}\left(s^{\prime}\right)\right] \end{aligned} $$

这同贝尔曼方程完全相同，因此 $v_{\pi}$ 一定与 $v_*$ 相同，$\pi$ 与 $\pi'$ 均必须为最优策略。因此，在除了原策略即为最优策略的情况下，策略改进一定会给出一个更优的结果。

策略迭代

一个策略 $\pi$ 根据 $v_{\pi}$ 产生了一个更好的策略 $\pi'$，进而我们可以通过计算 $v_{\pi'}$ 来得到一个更优的策略 $\pi''$。这样一个链式的方法可以得到一个不断改进的策略和价值函数序列：

$$ \pi_{0} \stackrel{E}{\longrightarrow} v_{\pi_{0}} \stackrel{I}{\longrightarrow} \pi_{1} \stackrel{E}{\longrightarrow} v_{\pi_{1}} \stackrel{I}{\longrightarrow} \pi_{2} \stackrel{E}{\longrightarrow} \cdots \stackrel{I}{\longrightarrow} \pi_{*} \stackrel{E}{\longrightarrow} v_{*} $$

其中 $\stackrel{E}{\longrightarrow}$ 表示策略评估，$\stackrel{I}{\longrightarrow}$ 表示策略改进。每一个策略都能保证同前一个一样或者更优，由于一个有限 MDP 必然只有有限种策略，所以在有限次的迭代后，这种方法一定收敛到一个最优的策略与最优价值函数。这种寻找最优策略的方法叫做策略迭代。整个策略迭代算法如下：

\begin{algorithm}
\caption{迭代策略算法}
\begin{algorithmic}
\FUNCTION{PolicyIteration}{}
\STATE \COMMENT{初始化}
\FOR{$s \in \mathcal{S}$}
  \STATE 初始化 $V \left(s\right) \in \mathbb{R}$
  \STATE 初始化 $\pi \left(s\right) \in \mathcal{A} \left(s\right)$
\ENDFOR
\WHILE{true}
  \STATE \COMMENT{策略评估}
  \REPEAT
    \STATE $\Delta \gets 0$
    \FOR{$s \in \mathcal{S}$}
      \STATE $v \gets V \left(s\right)$
      \STATE $V \left(s\right) \gets \sum_{s^{\prime}, r} p\left(s^{\prime}, r | s, \pi \left(s\right)\right)\left[r+\gamma V\left(s^{\prime}\right)\right]$
      \STATE $\Delta \gets \max\left(\Delta, \left|v - V \left(s\right)\right|\right)$
    \ENDFOR
  \UNTIL{$\Delta < \theta$}
  \STATE \COMMENT{策略改进}
  \STATE policy-stable $\gets$ true
  \FOR{$s \in \mathcal{S}$}
    \STATE $\pi' \left(s\right) \gets \pi \left(s\right)$
    \STATE $\pi \left(s\right) \gets \sum_{s^{\prime}, r} p\left(s^{\prime}, r | s, a\right)\left[r+\gamma V\left(s^{\prime}\right)\right]$
    \IF{$\pi' \left(s\right) \neq \pi \left(s\right)$}
      \STATE policy-stable $\gets$ flase
    \ENDIF
  \ENDFOR
  \IF{policy-stable $=$ true}
    \BREAK
  \ENDIF
\ENDWHILE
\RETURN $V, \pi$
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}

以杰克租车（Jack’s Car）问题为例：杰克在两地运营租车公司，每租出一辆车获得 10 元收益，为了保证每个地点有车可用，杰克需要夜间在两地之间移动车辆，每辆车的移动代价为 2 元。假设每个地点租车和还车的数量符合泊松分布 $\dfrac{\lambda^n}{n!} e^{- \lambda}$，其中 $\lambda$ 为期望值，租车的 $\lambda$ 在两地分别为 3 和 4，还车的 $\lambda$ 在两地分别为 3 和 2。假设任何一个地点不超过 20 辆车，每天最多移动 5 辆车，折扣率 $\gamma = 0.9$，将问题描述为一个持续的有限 MPD，时刻按天计算，状态为每天结束时每个地点的车辆数，动作则为夜间在两个地点之间移动的车辆数。策略从不移动任何车辆开始，整个策略迭代过程如下图所示：

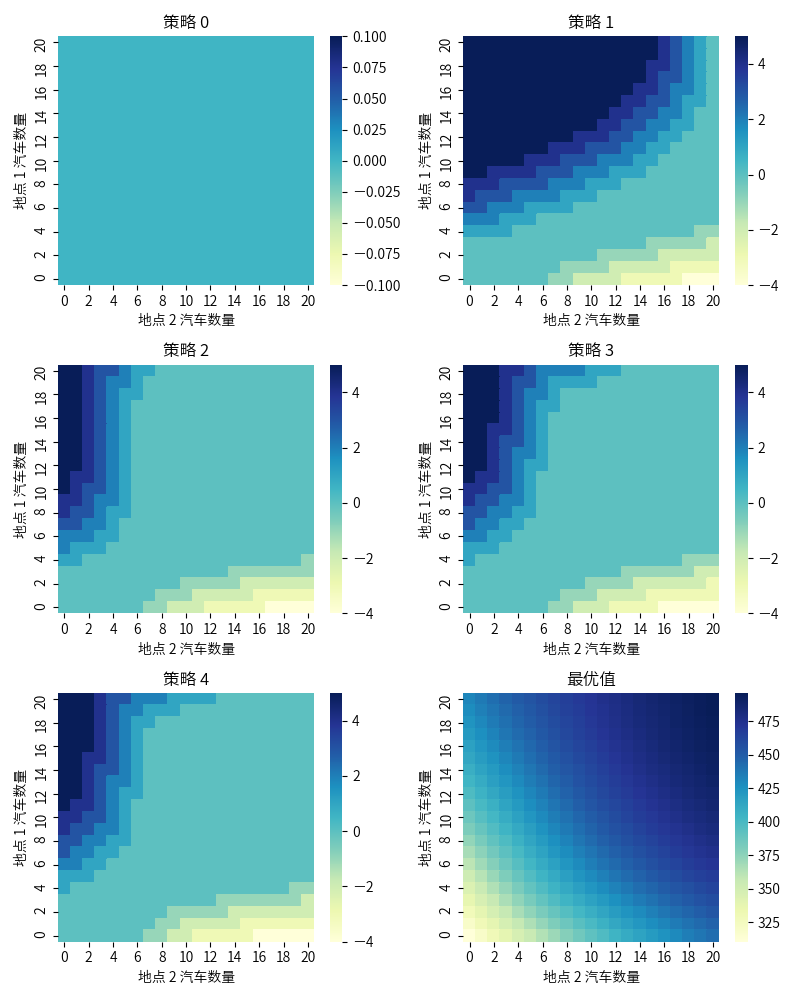
上例代码实现请参见这里。

价值迭代

策略迭代算法的一个缺点是每一次迭代都涉及了策略评估，这是一个需要多次遍历状态集合的迭代过程。如果策略评估是迭代进行的，那么收敛到 $v_{\pi}$ 理论上在极限处才成立，实际中不必等到其完全收敛，可以提前截断策略评估过程。有多种方式可以截断策略迭代中的策略评估步骤，并且不影响其收敛，一种重要的特殊情况是在一次遍历后即刻停止策略评估，该算法称为价值迭代。可以将此表示为结合了策略改进与阶段策略评估的简单更新公式，对任意 $s \in \mathcal{S}$：

$$ \begin{aligned} v_{k+1}(s) & \doteq \max _{a} \mathbb{E}\left[R_{t+1}+\gamma v_{k}\left(S_{t+1}\right) | S_{t}=s, A_{t}=a\right] \\ &=\max _{a} \sum_{s^{\prime}, r} p\left(s^{\prime}, r | s, a\right)\left[r+\gamma v_{k}\left(s^{\prime}\right)\right] \end{aligned} $$

可以证明，对任意 $v_0$，在 $v_*$ 存在的条件下，序列 $\left\{v_k\right\}$ 都可以收敛到 $v_*$。整个价值迭代算法如下：

\begin{algorithm}
\caption{价值迭代算法}
\begin{algorithmic}
\FUNCTION{ValueIteration}{}
\STATE \COMMENT{初始化}
\FOR{$s \in \mathcal{S}^{+}$}
  \STATE 初始化 $V \left(s\right)$，其中 $V \left(\text{终止状态}\right) = 0$
\ENDFOR
\STATE \COMMENT{价值迭代}
\REPEAT
  \STATE $\Delta \gets 0$
  \FOR{$s \in \mathcal{S}$}
    \STATE $v \gets V \left(s\right)$
    \STATE $V \left(s\right) \gets\sum_{s^{\prime}, r} p\left(s^{\prime}, r | s, a\right)\left[r+\gamma V\left(s^{\prime}\right)\right]$
    \STATE $\Delta \gets \max\left(\Delta, \left|v - V \left(s\right)\right|\right)$
  \ENDFOR
\UNTIL{$\Delta < \theta$}
\STATE 输出一个确定的策略 $\pi \approx \pi_*$ 使得 $\pi(s)=\arg \max _{a} \sum_{s^{\prime}, r} p\left(s^{\prime}, r | s, a\right)\left[r+\gamma V\left(s^{\prime}\right)\right]$
\RETURN $V, \pi$
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}

以**赌徒问题（Gambler’s Problem）**为例：一个赌徒下注猜一系列抛硬币实验的结果，如果正面朝上则获得这一次下注的钱，如果背面朝上则失去这一次下注的钱，游戏在达到目标收益 100 元或全部输光时结束。每抛一次硬币，赌徒必须从他的赌资中选取一个整数来下注，这个问题可以表示为一个非折扣的分幕式有限 MDP。状态为赌徒的赌资 $s \in \left\{1, 2, \cdots, 99\right\}$，动作为赌徒下注的金额 $a \in \left\{0, 1, \cdots, \min \left(s, 100 - s\right)\right\}$，收益在一般情况下为 0，只有在赌徒达到获利 100 元的终止状态时为 1。

令 $p_h$ 为抛硬币正面朝上的概率，如果 $p_h$ 已知，那么整个问题可以由价值迭代或其他类似算法解决。下图为当 $p_h = 0.4$ 时，价值迭代连续遍历得到的价值函数和最后的策略。

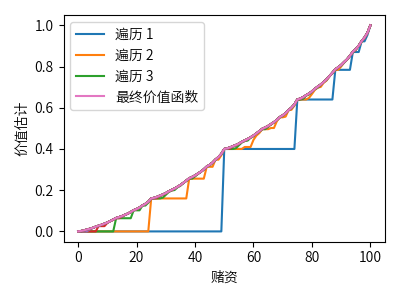
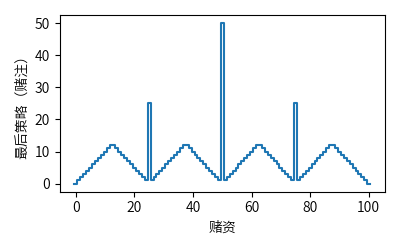
上例代码实现请参见这里。

异步动态规划

之前讨论的 DP 方法的一个主要缺点是它们涉及对 MDP 的整个状态集的操作，如果状态集很大，即使单次遍历也会十分昂贵。异步动态规划算法是一类就地迭代的 DP 算法，其不以系统遍历状态集的形式来组织算法。这些算法使用任意可用的状态值，以任意顺序来更新状态值，在某些状态的值更新一次之前，另一些状态的值可能已经更新了好几次。然而为了正确收敛，异步算法必须要不断地更新所有状态的值：在某个计算节点后，它不能忽略任何一个状态。

广义策略迭代

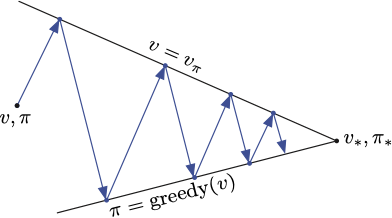
策略迭代包含两个同时进行的相互作用的流程，一个使得价值函数与当前策略一致（策略评估），另一个根据当前价值函数贪心地更新策略（策略改进）。在策略迭代中，这两个流程交替进行，每个流程都在另一个开始前完成。然而这也不是必须的，在异步方法中，评估和改进流程则以更细的粒度交替进行。我们利用**广义策略迭代（GPI）**一词来指代策略评估和策略改进相互作用的一般思路，与这两个流程的力度和其他细节无关。

几乎所有的强化学习方法都可以被描述为 GPI，几乎所有方法都包含明确定义的策略和价值函数。策略总是基于特定的价值函数进行改进，价值函数也始终会向对应特定策略的真实价值函数收敛。

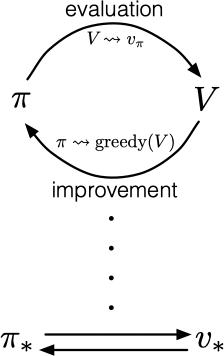
GPI 的评估和改进流程可以视为两个约束或目标之间的相互作用的流程。每个流程都把价值函数或策略推向其中的一条线，该线代表了对于两个目标中的某一个目标的解决方案，如下图所示：

「真诚赞赏，手留余香」

￥ 2 ￥ 5 ￥ 10 ￥ 50 ￥ 100 任意金额