文本相似度是指衡量两个文本的相似程度，相似程度的评价有很多角度：单纯的字面相似度（例如：我和他 v.s. 我和她），语义的相似度（例如：爸爸 v.s. 父亲）和风格的相似度（例如：我喜欢你 v.s. 我好喜欢你耶）等等。

文本表示角度

统计模型

文本切分

在中文和拉丁语系中，文本的直观表示就存在一定的差异，拉丁语系中词与词之间存在天然的分隔符，而中文则没有。

I can eat glass, it doesn’t hurt me.
我能吞下玻璃而不伤身体。

因此针对拉丁语系的文本切分相对中文容易许多。

• N 元语法

N-gram (N 元语法) 是一种文本表示方法，指文中连续出现的 $n$ 个词语。N-gram 模型是基于 $n-1$ 阶马尔科夫链的一种概率语言模型，可以通过前 $n-1$ 个词对第 $n$ 个词进行预测。以 南京市长江大桥 为例，N-gram 的表示如下：

一元语法（unigram）：南/京/市/长/江/大/桥
二元语法（bigram）：南京/京市/市长/长江/江大/大桥
三元语法（trigram）：南京市/京市长/市长江/长江大/江大桥

import re
from nltk.util import ngrams

s = '南京市长江大桥'
tokens = re.sub(r'\s', '', s)

list(ngrams(tokens, 1))
# [('南',), ('京',), ('市',), ('长',), ('江',), ('大',), ('桥',)]

list(ngrams(tokens, 2))
# [('南', '京'), ('京', '市'), ('市', '长'),
#  ('长', '江'), ('江', '大'), ('大', '桥')]

list(ngrams(tokens, 3, pad_left=True, pad_right=True, left_pad_symbol='<s>', right_pad_symbol='</s>'))
# [('<s>', '<s>', '南'),
#  ('<s>', '南', '京'),
#  ('南', '京', '市'),
#  ('京', '市', '长'),
#  ('市', '长', '江'),
#  ('长', '江', '大'),
#  ('江', '大', '桥'),
#  ('大', '桥', '</s>'),
#  ('桥', '</s>', '</s>')]

• 分词

分词就是将连续的字序列按照一定的规范重新组合成词序列的过程。在英文的行文中，单词之间是以空格作为自然分界符的，而中文只是字、句和段能通过明显的分界符来简单划界，唯独词没有一个形式上的分界符，虽然英文也同样存在短语的划分问题，不过在词这一层上，中文比之英文要复杂得多、困难得多。

s = '南京市长江大桥'

# jieba
# https://github.com/fxsjy/jieba
import jieba

list(jieba.cut(s, cut_all=False))
# ['南京市', '长江大桥']

list(jieba.cut(s, cut_all=True))
# ['南京', '南京市', '京市', '市长', '长江', '长江大桥', '大桥']

list(jieba.cut_for_search(s))
# ['南京', '京市', '南京市', '长江', '大桥', '长江大桥']

# THULAC
# https://github.com/thunlp/THULAC-Python
import thulac

thulac_ins = thulac.thulac()

thulac_ins.cut(s)
# [['南京市', 'ns'], ['长江', 'ns'], ['大桥', 'n']]

# PKUSEG
# https://github.com/lancopku/PKUSeg-python
import pkuseg

seg = pkuseg.pkuseg(postag=True)

seg.cut(s)
# [('南京市', 'ns'), ('长江', 'ns'), ('大桥', 'n')]

# HanLP
# https://github.com/hankcs/HanLP
import hanlp

tokenizer = hanlp.load('LARGE_ALBERT_BASE')

tokenizer(s)
# ['南京市', '长江', '大桥']

主题模型

除了对文本进行切分将切分后结果全部用于表示文本外，还可以用部分字词表示一篇文档。主题模型（Topic Model）在机器学习和自然语言处理等领域是用来在一系列文档中发现抽象主题的一种统计模型。

直观来讲，如果一篇文章有一个中心思想，那么一些特定词语会更频繁的出现。比方说，如果一篇文章是在讲狗的，那“狗”和“骨头”等词出现的频率会高些。如果一篇文章是在讲猫的，那“猫”和“鱼”等词出现的频率会高些。而有些词例如“这个”、“和”大概在两篇文章中出现的频率会大致相等。但真实的情况是，一篇文章通常包含多种主题，而且每个主题所占比例各不相同。因此，如果一篇文章 10% 和猫有关，90% 和狗有关，那么和狗相关的关键字出现的次数大概会是和猫相关的关键字出现次数的 9 倍。

一个主题模型试图用数学框架来体现文档的这种特点。主题模型自动分析每个文档，统计文档内的词语，根据统计的信息来断定当前文档含有哪些主题，以及每个主题所占的比例各为多少 ¹。

• TF-IDF

TF-IDF 是 Term Frequency - Inverse Document Frequency 的缩写，即“词频-逆文本频率”。TF-IDF 可以用于评估一个字词在语料中的一篇文档中的重要程度，基本思想是如果某个字词在一篇文档中出现的频率较高，而在其他文档中出现频率较低，则认为这个字词更能够代表这篇文档。

形式化地，对于文档 $y$ 中的字词 $x$ 的 TF-IDF 重要程度可以表示为：

$$ w_{x, y} = tf_{x, y} \times \log \left(\dfrac{N}{df_{x}}\right) $$

其中，$tf_{x, y}$ 表示字词 $x$ 在文档 $y$ 中出现的频率，$df_x$ 为包含字词 $x$ 的文档数量，$N$ 为语料中文档的总数量。

以 14 万歌词语料 为例，通过 TF-IDF 计算周杰伦的《简单爱》中最重要的 3 个词为 ['睡着', '放开', '棒球']。

• BM25

BM25 算法的全称为 Okapi BM25，是一种搜索引擎用于评估查询和文档之间相关程度的排序算法，其中 BM 是 Best Match 的缩写。

对于一个给定的查询 $Q$，包含的关键词为 $q_1, \cdots, q_n$，一个文档 $D$ 的 BM25 值定义为：

$$ \operatorname{score}(D, Q)=\sum_{i=1}^{n} \operatorname{IDF}\left(q_{i}\right) \cdot \frac{f\left(q_{i}, D\right) \cdot\left(k_{1}+1\right)}{f\left(q_{i}, D\right)+k_{1} \cdot\left(1-b+b \cdot \frac{|D|}{\text { avgdl }}\right)} $$

其中，$f\left(q_{i}, D\right)$ 表示 $q_i$ 在文档 $D$ 中的词频，$|D|$ 表示文档 $D$ 中的词数，$\text{avgdl}$ 表示语料中所有文档的平均长度。$k_1$ 和 $b$ 为自由参数，通常取值为 $k_1 \in \left[1.2, 2.0\right], b = 0.75$ ²。$\operatorname{IDF} \left(q_i\right)$ 表示词 $q_i$ 的逆文档频率，通常计算方式如下：

$$ \operatorname{IDF}\left(q_{i}\right)=\ln \left(\frac{N-n\left(q_{i}\right)+0.5}{n\left(q_{i}\right)+0.5}+1\right) $$

其中，$N$ 为语料中文档的总数量，$n \left(q_i\right)$ 表示包含 $q_i$ 的文档数量。

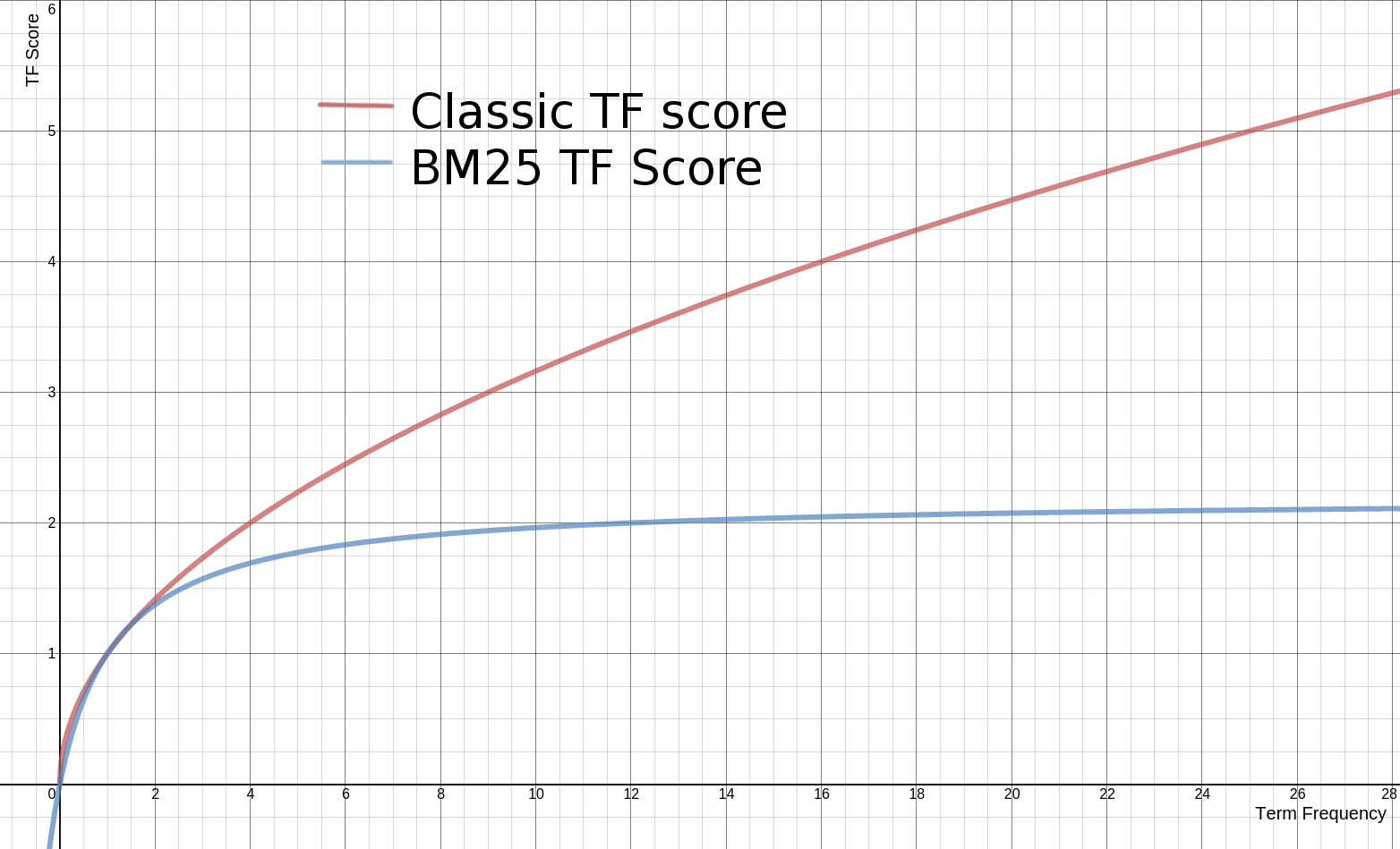
BM25 算法是对 TF-IDF 算法的优化，在词频的计算上，BM25 限制了文档 $D$ 中关键词 $q_i$ 的词频对评分的影响。为了防止词频过大，BM25 将这个值的上限设置为 $k_1 + 1$。

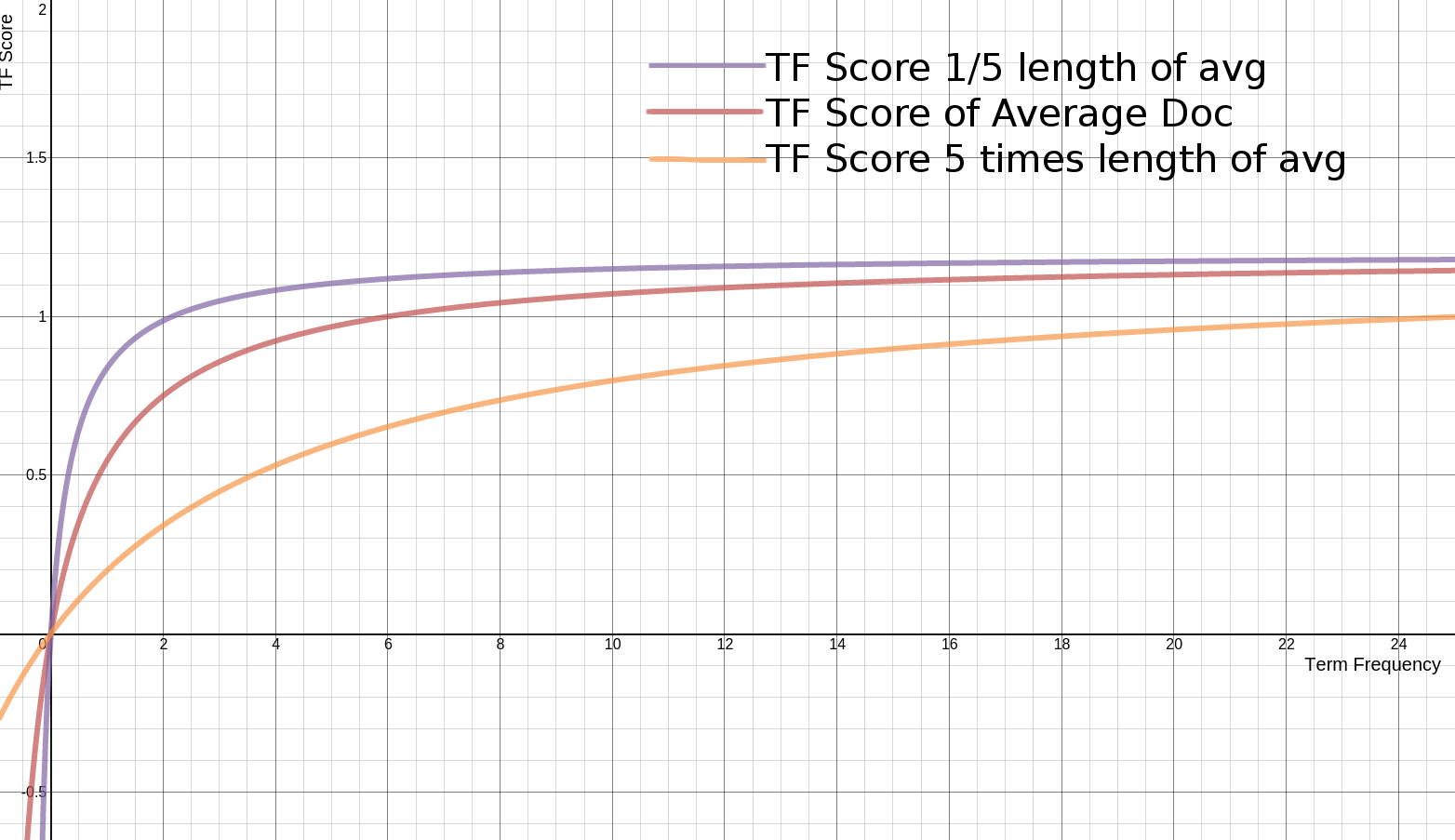
同时，BM25 还引入了平均文档长度 $\text{avgdl}$，不同的平均文档长度 $\text{avgdl}$ 对 TF 分值的影响如下图所示：

• TextRank

TextRank ³ 是基于 PageRank ⁴ 算法的一种关键词提取算法。PageRank 最早是用于 Google 的网页排名，因此以公司创始人拉里·佩奇（Larry Page）的姓氏来命名。PageRank 的计算公式如下：

$$ S\left(V_{i}\right)=(1-d)+d * \sum_{V_{j} \in I n\left(V_{i}\right)} \frac{1}{\left|O u t\left(V_{j}\right)\right|} S\left(V_{j}\right) $$

其中，$V_i$ 表示任意一个网页，$V_j$ 表示链接到网页 $V_i$ 的网页，$S \left(V_i\right)$ 表示网页 $V_i$ 的 PageRank 值，$In \left(V_i\right)$ 表示网页 $V_i$ 所有的入链集合，$Out \left(V_j\right)$ 表示网页 $V_j$ 所有的出链集合，$|\cdot|$ 表示集合的大小，$d$ 为阻尼系数，是为了确保每个网页的 PageRank 值都大于 0。

TextRank 由 PageRank 改进而来，计算公式如下：

$$ WS \left(V_{i}\right)=(1-d)+d * \sum_{V_{j} \in In\left(V_{i}\right)} \frac{w_{j i}}{\sum_{V_{k} \in Out\left(V_{j}\right)} w_{j k}} WS \left(V_{j}\right) $$

相比于 PageRank 公式增加了权重项 $W_{ji}$，用来表示两个节点之间的边的权重。TextRank 提取关键词的算法流程如下：

1. 将文本进行切分得到 $S_i = \left[t_{i1}, t_{i2}, \cdots, t_{in}\right]$。
2. 将 $S_i$ 中大小为 $k$ 的滑动窗口中的词定义为共现关系，构建关键词图 $G = \left(V, E\right)$。
3. 根据 TextRank 的计算公式对每个节点的值进行计算，直至收敛。
4. 对节点的 TextRank 的值进行倒叙排序，获取前 $n$ 个词作为关键词。

• LSA, PLSA, LDA & HDP

潜在语义分析（LSA, Latent Semantic Analysis）⁵ 的核心思想是将文本的高维词空间映射到一个低维的向量空间，我们称之为隐含语义空间。降维可以通过奇异值分解（SVD）实现，令 $X$ 表示语料矩阵，元素 $\left(i, j\right)$ 表示词 $i$ 和文档 $j$ 的共现情况（例如：词频）：

$$ X = \mathbf{d}_{j} \cdot \mathbf{t}_{i}^{T} = \left[\begin{array}{c} x_{1, j} \\ \vdots \\ x_{i, j} \\ \vdots \\ x_{m, j} \end{array}\right] \cdot \left[\begin{array}{ccccc} x_{i, 1} & \ldots & x_{i, j} & \ldots & x_{i, n} \end{array}\right] = \left[\begin{array}{ccccc} x_{1,1} & \ldots & x_{1, j} & \ldots & x_{1, n} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ x_{i, 1} & \ldots & x_{i, j} & \ldots & x_{i, n} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ x_{m, 1} & \ldots & x_{m, j} & \ldots & x_{m, n} \end{array}\right] $$

利用奇异值分解：

$$ X = U \Sigma V^{T} $$

取最大的 $K$ 个奇异值，则可以得到原始矩阵的近似矩阵：

$$ \widetilde{X} =U \widetilde{\Sigma} V^{T} $$

在处理一个新的文档时，可以利用下面的公式将原始的词空间映射到潜在语义空间：

$$ \tilde{x} =\tilde{\Sigma} ^{-1} V^{T} x_{test} $$

LSA 的优点：

1. 低维空间可以刻画同义词
2. 无监督模型
3. 降维可以减少噪声，使特征更加鲁棒

LSA 的缺点：

1. 未解决多义词问题
2. 计算复杂度高，增加新文档时需要重新训练
3. 没有明确的物理解释
4. 高斯分布假设不符合文本特征（词频不为负）
5. 维度的确定是 Ad hoc 的

概率潜语义分析（Probabilistic Latent Semantic Analysis, PLSA）⁶ 相比于 LSA 增加了概率模型，每个变量以及相应的概率分布和条件概率分布都有明确的物理解释。

PLSA 认为一篇文档可以由多个主题混合而成，而每个主题都是词上的概率分布，文章中的每个词都是由一个固定的主题生成的，如下图所示：

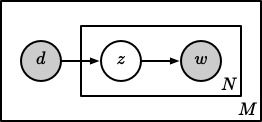
针对第 $m$ 篇文档 $d_m$ 中的每个词的生成概率为：

$$ p\left(w \mid d_{m}\right)=\sum_{z=1}^{K} p(w \mid z) p\left(z \mid d_{m}\right)=\sum_{z=1}^{K} \varphi_{z w} \theta_{m z} $$

因此整篇文档的生成概率为：

$$ p\left(\vec{w} \mid d_{m}\right)=\prod_{i=1}^{n} \sum_{z=1}^{K} p\left(w_{i} \mid z\right) p\left(z \mid d_{m}\right)=\prod_{i=1}^{n} \sum_{z=1}^{K} \varphi_{z w_{i}} \theta_{d z} $$

PLSA 可以利用 EM 算法求得局部最优解。

PLSA 优点：

1. 定义了概率模型，有明确的物理解释
2. 多项式分布假设更加符合文本特征
3. 可以通过模型选择和复杂度控制来确定主题的维度
4. 解决了同义词和多义词的问题

PLSA 缺点：

1. 随着文本和词的增加，PLSA 模型参数也随之线性增加
2. 可以生成语料中的文档的模型，但不能生成新文档的模型
3. EM 算法求解的计算量较大

隐含狄利克雷分布（Latent Dirichlet Allocation, LDA）⁷ 在 PLSA 的基础上增加了参数的先验分布。在 PLSA 中，对于一个新文档，是无法获取 $p \left(d\right)$ 的，因此这个概率模型是不完备的。LDA 对于 $\vec{\theta}_m$ 和 $\vec{\phi}_k$ 都增加了多项式分布的共轭分布狄利克雷分布作为先验，整个 LDA 模型如下图所示：

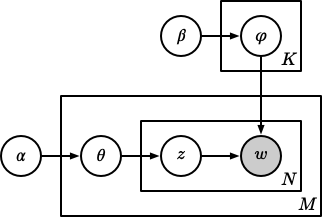
LDA 的参数估计可以通过吉布斯采样实现。PLSA 和 LDA 的更多细节请参见《LDA 数学八卦》⁸。

LDA 在使用过程中仍需要指定主题的个数，而层次狄利克雷过程（Hierarchical Dirichlet Processes, HDP）⁹ 通过过程的构造可以自动训练出主题的个数，更多实现细节请参考论文。

LSA，PLSA，LDA 和 HDP 之间的演化关系如下图所示：

本节相关代码详见 这里。

距离度量

本节内容源自 相似性和距离度量 (Similarity & Distance Measurement)。

相似性度量 (Similarity Measurement) 用于衡量两个元素之间的相似性程度或两者之间的距离 (Distance)。距离衡量的是指元素之间的不相似性 (Dissimilarity)，通常情况下我们可以利用一个距离函数定义集合 $X$ 上元素间的距离，即：

$$ d: X \times X \to \mathbb{R} $$

• Jaccard 系数

$$ s = \dfrac{\left|X \cap Y\right|}{\left| X \cup Y \right|} = \dfrac{\left|X \cap Y\right|}{\left|X\right| + \left|Y\right| - \left|X \cap Y\right|} $$

Jaccard 系数的取值范围为：$\left[0, 1\right]$，0 表示两个集合没有重合，1 表示两个集合完全重合。

• Dice 系数

$$ s = \dfrac{2 \left| X \cap Y \right|}{\left|X\right| + \left|Y\right|} $$

与 Jaccard 系数相同，Dice 系数的取值范围为：$\left[0, 1\right]$，两者之间可以相互转换 $s_d = 2 s_j / \left(1 + s_j\right), s_j = s_d / \left(2 - s_d\right)$。不同于 Jaccard 系数，Dice 系数的差异函数 $d = 1 - s$ 并不是一个合适的距离度量，因为其并不满足距离函数的三角不等式。

• Tversky 系数

$$ s = \dfrac{\left| X \cap Y \right|}{\left| X \cap Y \right| + \alpha \left| X \setminus Y \right| + \beta \left| Y \setminus X \right|} $$

其中，$X \setminus Y$ 表示集合的相对补集。Tversky 系数可以理解为 Jaccard 系数和 Dice 系数的一般化，当 $\alpha = \beta = 1$ 时为 Jaccard 系数，当 $\alpha = \beta = 0.5$ 时为 Dice 系数。

• Levenshtein 距离

Levenshtein 距离是 编辑距离 (Editor Distance) 的一种，指两个字串之间，由一个转成另一个所需的最少编辑操作次数。允许的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。例如将 kitten 转成 sitting，转换过程如下：

$$ \begin{equation*} \begin{split} \text{kitten} \to \text{sitten} \left(k \to s\right) \\ \text{sitten} \to \text{sittin} \left(e \to i\right) \\ \text{sittin} \to \text{sitting} \left(\ \to g\right) \end{split} \end{equation*} $$

编辑距离的求解可以利用动态规划的思想优化计算的时间复杂度。

• Jaro-Winkler 距离

对于给定的两个字符串 $s_1$ 和 $s_2$，Jaro 相似度定义为：

$$ sim = \begin{cases} 0 & \text{if} \ m = 0 \\ \dfrac{1}{3} \left(\dfrac{m}{\left|s_1\right|} + \dfrac{m}{\left|s_2\right|} + \dfrac{m-t}{m}\right) & \text{otherwise} \end{cases} $$

其中，$\left|s_i\right|$ 为字符串 $s_i$ 的长度，$m$ 为匹配的字符的个数，$t$ 换位数目的一半。如果字符串 $s_1$ 和 $s_2$ 相差不超过 $\lfloor \dfrac{\max \left(\left|s_1\right|, \left|s_2\right|\right)}{2} \rfloor - 1$，我们则认为两个字符串是匹配的。例如，对于字符串 CRATE 和 TRACE，仅 R, A, E 三个字符是匹配的，因此 $m = 3$，尽管 C, T 均出现在两个字符串中，但是他们的距离超过了 1 (即，$\lfloor \dfrac{5}{2} \rfloor - 1$)，因此 $t = 0$。

Jaro-Winkler 相似度给予了起始部分相同的字符串更高的分数，其定义为：

$$ sim_w = sim_j + l p \left(1 - sim_j\right) $$

其中，$sim_j$ 为字符串 $s_1$ 和 $s_2$ 的 Jaro 相似度，$l$ 为共同前缀的长度 (规定不超过 $4$)，$p$ 为调整系数 (规定不超过 $0.25$)，Winkler 将其设置为 $p = 0.1$。

• 汉明距离

汉明距离为两个等长字符串对应位置的不同字符的个数，也就是将一个字符串变换成另外一个字符串所需要替换的字符个数。例如：1011101 与 1001001 之间的汉明距离是 2，“toned” 与 “roses” 之间的汉明距离是 3。

import textdistance as td

s1 = '南京市长江大桥'
s2 = '北京市三元桥'

td.jaccard(s1, s2)
# 0.6666666666666666

td.sorensen_dice(s1, s2)
# 0.46153846153846156

td.tversky(s1, s2)
# 0.3

td.levenshtein(s1, s2)
# 4

td.jaro(s1, s2)
# 0.6428571428571429

td.hamming(s1, s2)
# 5

表示学习

基于表示学习的文本相似度计算方法的思路如下：

1. 利用表示学习方法将不定长的文本表示为定长的实值向量。
2. 计算转换后的实值向量相似度，用于表示两个文本的相似度。

关于文本表示学习和实值向量相似度计算请参见之前博客：词向量 (Word Embeddings)，相似性和距离度量 (Similarity & Distance Measurement)，预训练自然语言模型 (Pre-trained Models for NLP)。

文本词法，句法和语义角度

本节主要参考自《基于词法、句法和语义的句子相似度计算方法》¹⁰。

一段文本的内容分析由浅及深可以分为词法，句法和语义三个层次。

1. 词法，以词为对象，研究包括分词，词性和命名实体等。
2. 句法，以句子为对象，研究包括句子成分和句子结构等。
3. 语义，研究文字所表达的含义和蕴含的知识等。

词法和句法可以统一成为语法，如下图所示：

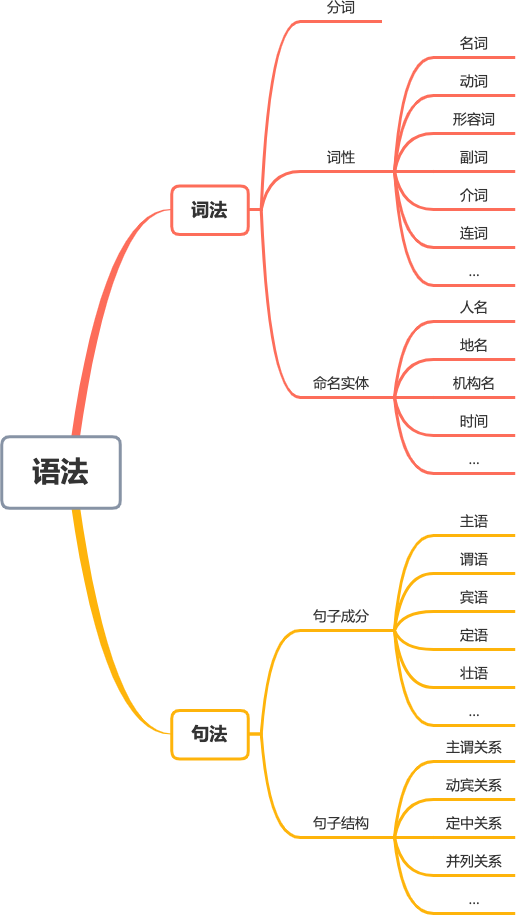
词法

词法层以单个句子作为输入，其输出为已标记（词性，命名实体等）的词汇序列。

词汇序列的相似度计算可以采用上文中的距离度量等方式实现。

句法

句法层用于研究句子各个组成部分及其排列顺序，将文本分解为句法单位，以理解句法元素的排列方式。句法层接收词法层分析后的将其转化为依存图。

对于依存图，我们可以利用三元组 $S = \left(V_1, E, V_2\right)$ 表示任意一个依存关系，然后通过统计计算两个文本的依存图的三元组集合之间的相似度来评价句法层的相似度。此外，也可以从树结构的角度直接评价依存句法的相似度，更多细节可参考相关论文 ^{11 12}。

语义

语义层用于研究文本所蕴含的意义。例如“父亲”和“爸爸”在词法层完全不同，但在语义层却具有相同的含义。针对语义相似度的两种深度学习范式如下：

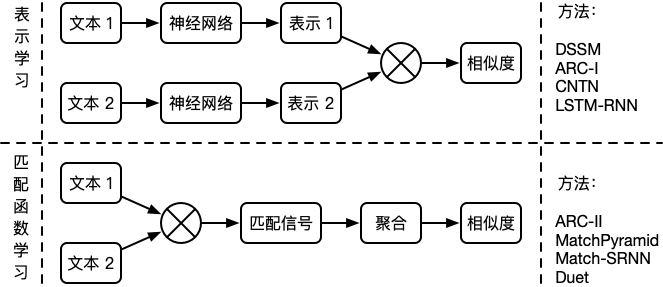
第一种范式首先通过神经网络获取文本的向量表示，再通过向量之间的相似度来衡量文本的语义相似度。这种范式在提取特征时不考虑另一个文本的信息，更适合做大规模的语义相似召回，例如：DSSM ¹³，ARC-I ¹⁴，CNTN ¹⁵，LSTM-RNN ¹⁶ 等。

第二种范式首先通过深度模型提取两个文本的交叉特征，得到匹配信号张量，再聚合为匹配分数。这种范式同时考虑两个文本的输入信息，更适合做小规模的语义相似精排，例如：ARC-II ¹⁴，MatchPyramid ¹⁷，Match-SRNN ¹⁸，Duet ¹⁹ 等。

文本长度角度

从文本长度角度出发，我们可以粗略的将文本分类为短文本和长文本。短文本包括“字词”，“短语”，“句子”等相对比较短的文本形式，长文本包括“段落”，“篇章”等相对比较长的文本形式。

短文本 v.s. 短文本

短文本同短文本的常见比较形式有：关键词（字词）同文本标题（句子）的匹配，相似查询（句子）的匹配等。如果单纯的希望获取字符层面的差异，可以通过距离度量进行相似度比较。如果需要从语义的角度获取相似度，则可以利用表示学习对需要比对的文本进行表示，在通过语义向量之间的相似程度来衡量原始文本之间的相似度，详情可参见上文。

短文本 v.s. 长文本

短文本同长文本的比较多见于文档的搜索，即给定相关的查询（字词），给出最相关的文档（段落和篇章）。对于这类问题常见的解决方式是对长文本利用 TF-IDF，BM25等方法或进行主题建模后，再同查询的关键词进行匹配计算相似度度。

长文本 v.s. 长文本

长文本同长文本的比较多见于文档的匹配和去重，对于这类问题常见的解决方式是利用关键词提取获取长文本的特征向量，然后利用特征向量之间的相似度衡量对应文本的相似程度。在针对海量文本的去重，还以应用 SimHash 等技术对文本生成一个指纹，从而实现快速去重。

「真诚赞赏，手留余香」

￥ 2 ￥ 5 ￥ 10 ￥ 50 ￥ 100 任意金额