你所应该知道的 A/B 测试 (A/B Test You Should Know)
范叶亮 / 2021-10-17
分类: 产品, 机器学习 / 标签: A/B 测试, A/B Test, 双盲测试, 流量分配, 正交实验, 互斥实验, 结果指标, 过程指标, 假设检验, 原假设, 备选假设, 第一类错误, 第二类错误, 显著水平, P 值, 置信度, 置信区间, 置信水平, 统计功效, A/A 测试 / 字数: 2771
什么是 A/B 测试
A/B 测试是一种随机测试,将两个不同的东西(即 A 和 B)进行假设比较。A/B 测试可以用来测试某一个变量两个不同版本的差异,一般是让 A 和 B 只有该变量不同,再测试目标对于 A 和 B 的反应差异,再判断 A 和 B 的方式何者较佳 1。A/B 测试的前身为双盲测试 2,在双盲测试中人员会被随机分为两组,受试验的对象及研究人员并不知道哪些对象属于对照组,哪些属于实验组,通过一段时间的实验后对比两组人员的结果是否有明显差异。在各种科学研究领域中,从医学、食品、心理到社会科学及法证都有使用双盲方法进行实验。
一个简单的 A/B 测试流程如下:

- 对目标人群进行随机划分,以进行有效的独立随机实验。
- 对不同分组应用不同的策略。
- 在确保实验有效的前提下,对不同分组的结果进行分析,以确定不同策略的优劣。
A/B 测试的主要目的是帮助我们更加科学的判断不同策略的优劣性,避免拍脑门的决策,不给杠精们互相 BATTLE 的机会。同时我们也需要认识到 A/B 测试只是一个工具,它能够帮助我们对产品和策略进行不断优化,但对产品和策略的创新更多还是需要洞察力。它可以让我们在已达到的山上越来越高,却不能用它来发现一座新的山脉。一句话:A/B 测试不是万能的,但离开 A/B 测试是万万不能的。
A/B 测试的科学性
流量分配
进行 A/B 测试的第一个问题就是如何划分用户,如果采用上面简单五五开的方式我们一次只能做一个实验,当我们需要同时做多个实验时就无法满足了。如果对用户分成多个桶,当桶的数量过多时,每个桶中的用户数量就会过少,从而会导致实验的置信度下降。
为了保证可以使用相同的流量开展不同的实验,同时各个实验之间不能相关干扰,我们需要采用正交实验。正交实验的思想如下:
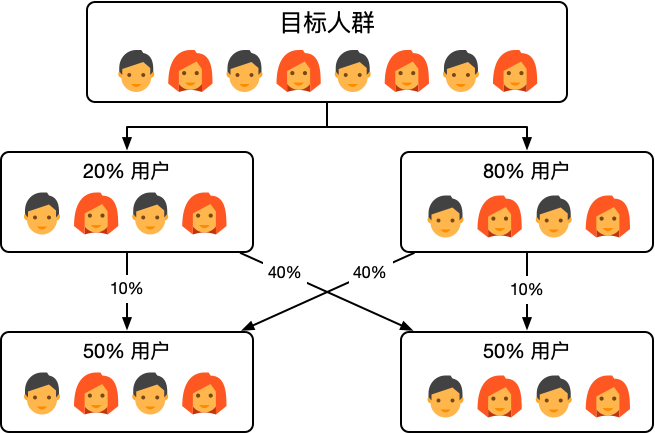
每个独立实验为一层,层与层之间的流量是正交的,流量经过一层实验后会再次被随机打散。
有些情况下实验并不是独立的,例如同时对按钮和背景的颜色进行实验,按钮和背景颜色之间并不是独立的(即有些按钮和背景颜色搭配从设计角度是不可行的,没有必要进行实验),这种情况下我们需要采用互斥实验。互斥实验的思想如下:

实验在同一层进行流量拆分,不同组之间的流量是没有重叠的。
在 A/B 测试中,当多个实验内容相互影响应选择互斥方法分配流量,当多个实验内容不会相互影响应选择正交方法分配流量。更加精细的流量分类和控制可以参考 Google 的论文 Overlapping Experiment Infrastructure: More, Better, Faster Experimentation 3。
评价指标选择
在设计实验之前我们需要明确实验的目标,根据目标才能确定合理的评价指标。更多情况下我们应该从业务的视角出发选择合适的评价指标,我们以风险策略模型实验为例,我们可以从技术和业务角度选择不同的评价指标:
- 技术角度:准确率和召回率
- 业务角度:客诉率和追损金额
单纯从技术角度出发我们会忽视很多现实问题,例如两个策略的准确率和召回率差不多,但识别的结果人群不一样,这些人造成的损失也可能不一样。因此能够帮助我们追回更多损失同时有更小的客诉率才是更优的策略。
在进行实验时结果指标至关重要,但有时我们也应该关注一些过程指标。以页面优化实验为例,可能的过程指标和结果指标有:
- 过程指标:页面平均停留时间,页面跳出率等
- 结果指标:商品加购率,商品转化率等
策略和模型最终都是要为业务服务的,因此我们应常关注业务指标,一些常用的业务指标有:点击率(CTR)、转化率(CVR)、千次展示收入(RPM)等。
有效性检验
当实验完成得到结果后,我们还需要判断实验结果是否有效,这部分主要依靠统计学中的假设检验进行分析。针对两个实验在确定合理的统计量后,需要构建如下两个假设:
- 原假设 $H_0$:两个实验的统计量无差异
- 备选假设 $H_1$:两个实验的统计量有差异
对于假设检验只可能有两种结果:一个是接受原假设,一个是拒绝原假设。在进行假设检验过程中,容易犯两类错误:
| 是否接受原假设 \ 假设真伪 | $H_0$ 为真 | $H_1$ 为真 |
|---|---|---|
| 拒绝原假设 | 第一类错误 $\alpha$:显著水平 |
正确决策 $1 - \alpha$:置信度 |
| 接受原假设 | 正确决策 $1 - \beta$:统计功效 |
第二类错误 $\beta$ |
第一类错误(弃真)即原假设为真时拒绝原假设,犯第一类错误的概率为 $\alpha$,即显著水平。第二类错误(取伪)即原假设为假时未拒绝原假设,犯第二类错误的概率为 $\beta$。
在进行有效性检验时我们有多个指标可以参考:
- P 值。P 值就是当原假设为真时,比所得到的样本观察结果更极端的结果出现的概率。如果 P 值很小,说明原假设情况的发生的概率很小,而如果出现了,根据小概率原理,我们就有理由拒绝原假设,P 值越小,我们拒绝原假设的理由越充分。
- 置信区间。置信区间就是分别以统计量的置信上限和置信下限为上下界构成的区间。置信水平是指包含总体平均值的概率是多大,例如:95% 的置信水平表示,如果有 100 个样本,可以构造出 100 个这样的区间,有 95% 的可能性包含总体平均值。在 A/B 测试时,如果置信区间上下限的值同为正或负,则认为存在有显著差异的可能性;如果同时有正值和负值,则认为不存在有显著差异的可能性。
- 统计功效。一般情况下我们希望拒绝原假设,得到新的结论,即在进行 A/B 测试时希望实验组的效果优于对照组。也就是我们希望不要出现在应该拒绝原假设时却没有拒绝的情况,即犯第二类错误。统计功效就是我们没有犯第二类错误的概率 $1 - \beta$,在进行 A/B 测试时表示当两个策略之间存在显著差异时,实验能正确做出存在差异判断的概率。
综上,我们可以认为当 A/B 测试实验数据在 95% 的置信水平区间内,P 值小于0.05,功效大于 80% 的情况下,实验结果是可信赖的。
A/A 测试
在做 A/B 测试的时候,有时尽管我们发现 A/B 两组有明显差异,但我们依旧无法确认这种差异是由于实验条件不同还是 A/B 两组用户本身的差异带来的。尽管 A/B 两组用户是随机抽样,但两组用户在空跑期(即实验条件一致)也会出现显著差异。因此为了避免这个问题,我们会选择进行 A/A 测试,即在正式开启实验之前,先进行一段时间的空跑,对 A/B 两组用户采用同样的实验条件,一段时间后,再看两组之间的差异。如果差异显著,数据弃之不用,重新选组。如果差异不显著,记录两组之间的均值差,然后在实验期结束时,用实验期的组间差异减去空跑期的组间差异得到最终实验结果。
A/A 测试也会存在一些局限,在实际情况中,组间差异是一定存在。因此在这个前提下,可以用统计方式来衡量差异大小,在计算实验效果的时候,把差异考虑在内即可。差异产生的主要原因就是“随机性”,我们同样可以利用置信度和置信区间来描述 A/A 实验的波动。在进行实验时直接进行 A/B 测试,不需要考虑 A/A 测试,在分析结果时,需要考虑 A/B 测试实验之间的差异要大于 A/A 测试实验之间的差异。
-
Tang, Diane, et al. “Overlapping experiment infrastructure: More, better, faster experimentation.” Proceedings of the 16th ACM SIGKDD international conference on Knowledge discovery and data mining. 2010. ↩︎